Statistics/Displaying Data/Pie Charts
Pie Charts[edit | edit source]
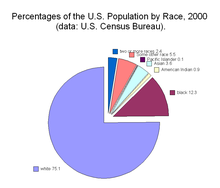
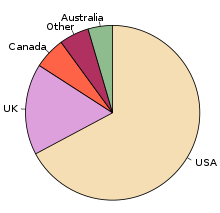
A Pie-Chart/Diagram is a graphical device - a circular shape broken into sub-divisions. The sub-divisions are called "sectors", whose areas are proportional to the various parts into which the whole quantity is divided. The sectors may be coloured differently to show the relationship of parts to the whole. A pie diagram is an alternative of the sub-divided bar diagram.
To construct a pie-chart, first we draw a circle of any suitable radius then the whole quantity which is to be divided is equated to 360 degrees. The different parts of the circle in terms of angles are calculated by the following formula.
Component Value / Whole Quantity * 360
The component parts i.e. sectors have been cut beginning from top in clockwise order.
Note that the percentages in a list may not add up to exactly 100% due to rounding. For example if a person spends a third of their time on each of three activities: 33%, 33% and 33% sums to 99%.
Warning: Pie charts are a poor way of communicating information. The eye is good at judging linear measures and bad at judging relative areas. A bar chart or dot chart is a preferable way of displaying this type of data.
Cleveland (1985), page 264: "Data that can be shown by pie charts always can be shown by a dot chart. This means that judgements of position along a common scale can be made instead of the less accurate angle judgments." This statement is based on the empirical investigations of Cleveland and McGill as well as investigations by perceptual psychologists.
Three-dimensional (3d) pie charts compound perceptual misinterpretation of statistical information by altering the relative angle of pie slices to create the impression of depth into a vanishing point. Angles and areas at the bottom of the chart must be exaggerated and the angles and areas at the top of the chart reduced in order to create the dimensional effect; a specifically false depiction of the data.
External Links