Sensory Systems/Auditory System
| This page may need to verify facts by citing reliable publications. You can help by adding references to reliable publications, or by correcting statements cited as fact. |
Introduction
[edit | edit source]The sensory system for the sense of hearing is the auditory system. This wikibook covers the physiology of the auditory system, and its application to the most successful neurosensory prosthesis - cochlear implants. The physics and engineering of acoustics are covered in a separate wikibook, Acoustics. An excellent source of images and animations is "Journey into the world of hearing" [1].
The ability to hear is not found as widely in the animal kingdom as other senses like touch, taste and smell. It is restricted mainly to vertebrates and insects.[citation needed] Within these, mammals and birds have the most highly developed sense of hearing. The table below shows frequency ranges of humans and some selected animals:[citation needed]
| Humans | 20-20'000 Hz |
|---|---|
| Whales | 20-100'000 Hz |
| Bats | 1'500-100'000 Hz |
| Fish | 20-3'000 Hz |
The organ that detects sound is the ear. It acts as receiver in the process of collecting acoustic information and passing it through the nervous system into the brain. The ear includes structures for both the sense of hearing and the sense of balance. It does not only play an important role as part of the auditory system in order to receive sound but also in the sense of balance and body position.
 |
 |
 |
 |
Humans have a pair of ears placed symmetrically on both sides of the head which makes it possible to localize sound sources. The brain extracts and processes different forms of data in order to localize sound, such as:
- the shape of the sound spectrum at the tympanic membrane (eardrum)
- the difference in sound intensity between the left and the right ear
- the difference in time-of-arrival between the left and the right ear
- the difference in time-of-arrival between reflections of the ear itself (this means in other words: the shape of the pinna (pattern of folds and ridges) captures sound-waves in a way that helps localizing the sound source, especially on the vertical axis.
Healthy, young humans are able to hear sounds over a frequency range from 20 Hz to 20 kHz.[citation needed] We are most sensitive to frequencies between 2000 and 4000 Hz[citation needed] which is the frequency range of spoken words. The frequency resolution is 0.2%[citation needed] which means that one can distinguish between a tone of 1000 Hz and 1002 Hz. A sound at 1 kHz can be detected if it deflects the tympanic membrane (eardrum) by less than 1 Angstrom[citation needed], which is less than the diameter of a hydrogen atom. This extreme sensitivity of the ear may explain why it contains the smallest bone that exists inside a human body: the stapes (stirrup). It is 0.25 to 0.33 cm long and weighs between 1.9 and 4.3 mg.[citation needed]
The following video provides an overview of the concepts that will be presented in more detail in the next sections.
Anatomy of the Auditory System
[edit | edit source]
The aim of this section is to explain the anatomy of the auditory system of humans. The chapter illustrates the composition of auditory organs in the sequence that acoustic information proceeds during sound perception.
Please note that the core information for “Sensory Organ Components” can also be found on the Wikipedia page “Auditory system”, excluding some changes like extensions and specifications made in this article. (see also: Wikipedia Auditory system)
The auditory system senses sound waves, that are changes in air pressure, and converts these changes into electrical signals. These signals can then be processed, analyzed and interpreted by the brain. For the moment, let's focus on the structure and components of the auditory system. The auditory system consists mainly of two parts:
- the ear and
- the auditory nervous system (central auditory system)
The ear
[edit | edit source]The ear is the organ where the first processing of sound occurs and where the sensory receptors are located. It consists of three parts:
- outer ear
- middle ear
- inner ear
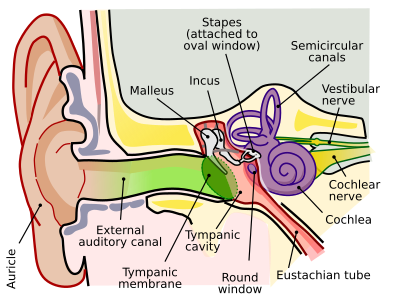
Outer ear
[edit | edit source]Function: Gathering sound energy and amplification of sound pressure.
The folds of cartilage surrounding the ear canal (external auditory meatus, external acoustic meatus) are called the pinna. It is the visible part of the ear. Sound waves are reflected and attenuated when they hit the pinna, and these changes provide additional information that will help the brain determine the direction from which the sounds came. The sound waves enter the auditory canal, a deceptively simple tube. The ear canal amplifies sounds that are between 3 and 12 kHz. At the far end of the ear canal is the tympanic membrane (eardrum), which marks the beginning of the middle ear.
Middle ear
[edit | edit source]
Function: Transmission of acoustic energy from air to the cochlea.
Sound waves traveling through the ear canal will hit the tympanic membrane (tympanum, eardrum). This wave information travels across the air-filled tympanic cavity (middle ear cavity) via a series of bones: the malleus (hammer), incus (anvil) and stapes (stirrup). These ossicles act as a lever and a teletype, converting the lower-pressure eardrum sound vibrations into higher-pressure sound vibrations at another, smaller membrane called the oval (or elliptical) window, which is one of two openings into the cochlea of the inner ear. The second opening is called round window. It allows the fluid in the cochlea to move.
The malleus articulates with the tympanic membrane via the manubrium, whereas the stapes articulates with the oval window via its footplate. Higher pressure is necessary because the inner ear beyond the oval window contains liquid rather than air. The sound is not amplified uniformly across the ossicular chain. The stapedius reflex of the middle ear muscles helps protect the inner ear from damage.
The middle ear still contains the sound information in wave form; it is converted to nerve impulses in the cochlea.
Inner ear
[edit | edit source]| Structural diagram of the cochlea | Cross section of the cochlea | Cochlea and Vestibular System from an MRI scan |
|---|---|---|
 |
 |

|
Function: Transformation of mechanical waves (sound) into electric signals (neural signals).
The inner ear consists of the cochlea and several non-auditory structures. The cochlea is a snail-shaped part of the inner ear. It has three fluid-filled sections: scala tympani (lower gallery), scala media (middle gallery, cochlear duct) and scala vestibuli (upper gallery). The cochlea supports a fluid wave driven by pressure across the basilar membrane separating two of the sections (scala tympani and scala media). The basilar membrane is about 3 cm long and between 0.5 to 0.04 mm wide. Reissner’s membrane (vestibular membrane) separates scala media and scala vestibuli.
The scala media contains an extracellular fluid called endolymph, also known as Scarpa's Fluid after Antonio Scarpa. The organ of Corti is located in this duct, and transforms mechanical waves to electric signals in neurons. The other two sections, scala tympani and scala vestibuli, are located within the bony labyrinth which is filled with fluid called perilymph. The chemical difference between the two fluids endolymph (in scala media) and perilymph (in scala tympani and scala vestibuli) is important for the function of the inner ear.
Organ of Corti
[edit | edit source]The organ of Corti forms a ribbon of sensory epithelium which runs lengthwise down the entire cochlea. The hair cells of the organ of Corti transform the fluid waves into nerve signals. The journey of a billion nerves begins with this first step; from here further processing leads to a series of auditory reactions and sensations.
Transition from ear to auditory nervous system
[edit | edit source]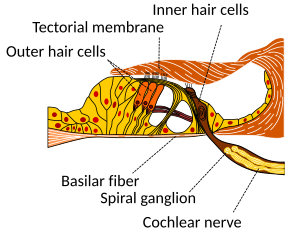
Hair cells
[edit | edit source]Hair cells are columnar cells, each with a bundle of 100-200 specialized cilia at the top, for which they are named. These cilia are the mechanosensors for hearing. The shorter ones are called stereocilia, and the longest one at the end of each haircell bundle kinocilium. The location of the kinocilium determine the on-direction, i.e. the direction of deflection inducing the maximum hair cell excitation. Lightly resting atop the longest cilia is the tectorial membrane, which moves back and forth with each cycle of sound, tilting the cilia and allowing electric current into the hair cell.
The function of hair cells is not fully established up to now. Currently, the knowledge of the function of hair cells allows to replace the cells by cochlear implants in case of hearing lost. However, more research into the function of the hair cells may someday even make it possible for the cells to be repaired. The current model is that cilia are attached to one another by “tip links”, structures which link the tips of one cilium to another. Stretching and compressing, the tip links then open an ion channel and produce the receptor potential in the hair cell. Note that a deflection of 100 nanometers already elicits 90% of the full receptor potential.
Neurons
[edit | edit source]The nervous system distinguishes between nerve fibres carrying information towards the central nervous system and nerve fibres carrying the information away from it:
- Afferent neurons (also sensory or receptor neurons) carry nerve impulses from receptors (sense organs) towards the central nervous system
- Efferent neurons (also motor or effector neurons) carry nerve impulses away from the central nervous system to effectors such as muscles or glands (and also the ciliated cells of the inner ear)
Afferent neurons innervate cochlear inner hair cells, at synapses where the neurotransmitter glutamate communicates signals from the hair cells to the dendrites of the primary auditory neurons.
There are far fewer inner hair cells in the cochlea than afferent nerve fibers. The neural dendrites belong to neurons of the auditory nerve, which in turn joins the vestibular nerve to form the vestibulocochlear nerve, or cranial nerve number VIII'
Efferent projections from the brain to the cochlea also play a role in the perception of sound. Efferent synapses occur on outer hair cells and on afferent (towards the brain) dendrites under inner hair cells.
Auditory nervous system
[edit | edit source]The sound information, now re-encoded in form of electric signals, travels down the auditory nerve (acoustic nerve, vestibulocochlear nerve, VIIIth cranial nerve), through intermediate stations such as the cochlear nuclei and superior olivary complex of the brainstem and the inferior colliculus of the midbrain, being further processed at each waypoint. The information eventually reaches the thalamus, and from there it is relayed to the cortex. In the human brain, the primary auditory cortex is located in the temporal lobe.
Primary auditory cortex
[edit | edit source]The primary auditory cortex is the first region of cerebral cortex to receive auditory input.
Perception of sound is associated with the right posterior superior temporal gyrus (STG). The superior temporal gyrus contains several important structures of the brain, including Brodmann areas 41 and 42, marking the location of the primary auditory cortex, the cortical region responsible for the sensation of basic characteristics of sound such as pitch and rhythm.
The auditory association area is located within the temporal lobe of the brain, in an area called the Wernicke's area, or area 22. This area, near the lateral cerebral sulcus, is an important region for the processing of acoustic signals so that they can be distinguished as speech, music, or noise.
Auditory Signal Processing
[edit | edit source]Now that the anatomy of the auditory system has been sketched out, this topic goes deeper into the physiological processes which take place while perceiving acoustic information and converting this information into data that can be handled by the brain. Hearing starts with pressure waves hitting the auditory canal and is finally perceived by the brain. This section details the process transforming vibrations into perception.
Effect of the head
[edit | edit source]Sound waves with a wavelength shorter than the head produce a sound shadow on the ear further away from the sound source. When the wavelength is longer than the head, diffraction of the sound leads to approximately equal sound intensities on both ears.

Sound reception at the pinna
[edit | edit source]The pinna collects sound waves in air affecting sound coming from behind and the front differently with its corrugated shape. The sound waves are reflected and attenuated or amplified. These changes will later help sound localization.
In the external auditory canal, sounds between 3 and 12 kHz - a range crucial for human communication - are amplified. It acts as resonator amplifying the incoming frequencies.
Sound conduction to the cochlea
[edit | edit source]Sound that entered the pinna in form of waves travels along the auditory canal until it reaches the beginning of the middle ear marked by the tympanic membrane (eardrum). Since the inner ear is filled with fluid, the middle ear is kind of an impedance matching device in order to solve the problem of sound energy reflection on the transition from air to the fluid. As an example, on the transition from air to water 99.9% of the incoming sound energy is reflected. This can be calculated using:
with Ir the intensity of the reflected sound, Ii the intensity of the incoming sound and Zk the wave resistance of the two media ( Zair = 414 kg m-2 s-1 and Zwater = 1.48*106 kg m-2 s-1). Three factors that contribute the impedance matching are:
- the relative size difference between tympanum and oval window
- the lever effect of the middle ear ossicles and
- the shape of the tympanum.

The longitudinal changes in air pressure of the sound-wave cause the tympanic membrane to vibrate which, in turn, makes the three chained ossicles malleus, incus and stirrup oscillate synchronously. These bones vibrate as a unit, elevating the energy from the tympanic membrane to the oval window. In addition, the energy of sound is further enhanced by the areal difference between the membrane and the stapes footplate. The middle ear acts as an impedance transformer by changing the sound energy collected by the tympanic membrane into greater force and less excursion. This mechanism facilitates transmission of sound-waves in air into vibrations of the fluid in the cochlea. The transformation results from the pistonlike in- and out-motion by the footplate of the stapes which is located in the oval window. This movement performed by the footplate sets the fluid in the cochlea into motion.
Through the stapedius muscle, the smallest muscle in the human body, the middle ear has a gating function: contracting this muscle changes the impedance of the middle ear, thus protecting the inner ear from damage through loud sounds.
Frequency analysis in the cochlea
[edit | edit source]The three fluid-filled compartements of the cochlea (scala vestibuli, scala media, scala tympani) are separated by the basilar membrane and the Reissner’s membrane. The function of the cochlea is to separate sounds according to their spectrum and transform it into a neural code.
When the footplate of the stapes pushes into the perilymph of the scala vestibuli, as a consequence the membrane of Reissner bends into the scala media. This elongation of Reissner’s membrane causes the endolymph to move within the scala media and induces a displacement of the basilar membrane.
The separation of the sound frequencies in the cochlea is due to the special properties of the basilar membrane. The fluid in the cochlea vibrates (due to in- and out-motion of the stapes footplate) setting the membrane in motion like a traveling wave. The wave starts at the base and progresses towards the apex of the cochlea. The transversal waves in the basilar membrane propagate with
with μ the shear modulus and ρ the density of the material. Since width and tension of the basilar membrane change, the speed of the waves propagating along the membrane changes from about 100 m/s near the oval window to 10 m/s near the apex.
There is a point along the basilar membrane where the amplitude of the wave decreases abruptly. At this point, the sound wave in the cochlear fluid produces the maximal displacement (peak amplitude) of the basilar membrane. The distance the wave travels before getting to that characteristic point depends on the frequency of the incoming sound. Therefore each point of the basilar membrane corresponds to a specific value of the stimulating frequency. A low-frequency sound travels a longer distance than a high-frequency sound before it reaches its characteristic point. Frequencies are scaled along the basilar membrane with high frequencies at the base and low frequencies at the apex of the cochlea.

Identifying frequency by the location of the maximum displacement of the basilar membrane is called tonotopic encoding of frequency. It automatically solves two problems:
- It automatically parallelizes the subsequent processing of frequency. This tonotopic encoding is maintained all the way up to the cortex.
- Our nervous system transmits information with action potentials, which are limited to less than 500 Hz. Through tonotopic encoding, also higher frequencies can be accurately represented.
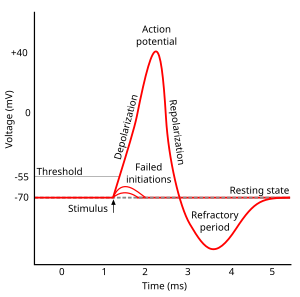
Sensory transduction in the cochlea
[edit | edit source]Most everyday sounds are composed of multiple frequencies. The brain processes the distinct frequencies, not the complete sounds. Due to its inhomogeneous properties, the basilar membrane is performing an approximation to a Fourier transform. The sound is thereby split into its different frequencies, and each hair cell on the membrane corresponds to a certain frequency. The loudness of the frequencies is encoded by the firing rate of the corresponding afferent fiber. This is due to the amplitude of the traveling wave on the basilar membrane, which depends on the loudness of the incoming sound.



The sensory cells of the auditory system, known as hair cells, are located along the basilar membrane within the organ of Corti. Each organ of Corti contains about 16,000 such cells, innervated by about 30,000 afferent nerve fibers. There are two anatomically and functionally distinct types of hair cells: the inner and the outer hair cells. Along the basilar membrane these two types are arranged in one row of inner cells and three to five rows of outer cells. Most of the afferent innervation comes from the inner hair cells while most of the efferent innervation goes to the outer hair cells. The inner hair cells influence the discharge rate of the individual auditory nerve fibers that connect to these hair cells. Therefore inner hair cells transfer sound information to higher auditory nervous centers. The outer hair cells, in contrast, amplify the movement of the basilar membrane by injecting energy into the motion of the membrane and reducing frictional losses but do not contribute in transmitting sound information. The motion of the basilar membrane deflects the stereocilias (hairs on the hair cells) and causes the intracellular potentials of the hair cells to decrease (depolarization) or increase (hyperpolarization), depending on the direction of the deflection. When the stereocilias are in a resting position, there is a steady state current flowing through the channels of the cells. The movement of the stereocilias therefore modulates the current flow around that steady state current.
Let's look at the modes of action of the two different hair cell types separately:
- Inner hair cells:
The deflection of the hair-cell stereocilia opens mechanically gated ion channels that allow small, positively charged potassium ions (K+) to enter the cell and causing it to depolarize. Unlike many other electrically active cells, the hair cell itself does not fire an action potential. Instead, the influx of positive ions from the endolymph in scala media depolarizes the cell, resulting in a receptor potential. This receptor potential opens voltage gated calcium channels; calcium ions (Ca2+) then enter the cell and trigger the release of neurotransmitters at the basal end of the cell. The neurotransmitters diffuse across the narrow space between the hair cell and a nerve terminal, where they then bind to receptors and thus trigger action potentials in the nerve. In this way, neurotransmitter increases the firing rate in the VIIIth cranial nerve and the mechanical sound signal is converted into an electrical nerve signal.
The repolarization in the hair cell is done in a special manner. The perilymph in Scala tympani has a very low concentration of positive ions. The electrochemical gradient makes the positive ions flow through channels to the perilymph. (see also: Wikipedia Hair cell)
- Outer hair cells:
In humans' outer hair cells, the receptor potential triggers active vibrations of the cell body. This mechanical response to electrical signals is termed somatic electromotility and drives oscillations in the cell’s length, which occur at the frequency of the incoming sound and provide mechanical feedback amplification. Outer hair cells have evolved only in mammals. Without functioning outer hair cells the sensitivity decreases by approximately 50 dB (due to greater frictional losses in the basilar membrane which would damp the motion of the membrane). They have also improved frequency selectivity (frequency discrimination), which is of particular benefit for humans, because it enables sophisticated speech and music. (see also: Wikipedia Hair cell)
With no external stimulation, auditory nerve fibres discharge action potentials in a random time sequence. This random time firing is called spontaneous activity. The spontaneous discharge rates of the fibers vary from very slow rates to rates of up to 100 per second. Fibers are placed into three groups depending on whether they fire spontaneously at high, medium or low rates. Fibers with high spontaneous rates (> 18 per second) tend to be more sensitive to sound stimulation than other fibers.
Auditory pathway of nerve impulses
[edit | edit source]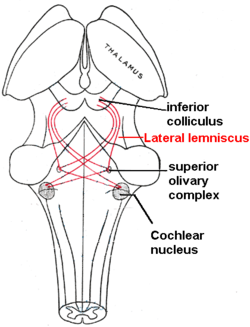
So in the inner hair cells the mechanical sound signal is finally converted into electrical nerve signals. The inner hair cells are connected to auditory nerve fibres whose nuclei form the spiral ganglion. In the spiral ganglion the electrical signals (electrical spikes, action potentials) are generated and transmitted along the cochlear branch of the auditory nerve (VIIIth cranial nerve) to the cochlear nucleus in the brainstem.
From there, the auditory information is divided into at least two streams:
- Ventral Cochlear Nucleus:
One stream is the ventral cochlear nucleus which is split further into the posteroventral cochlear nucleus (PVCN) and the anteroventral cochlear nucleus (AVCN). The ventral cochlear nucleus cells project to a collection of nuclei called the superior olivary complex.
Superior olivary complex: Sound localization
[edit | edit source]The superior olivary complex - a small mass of gray substance - is believed to be involved in the localization of sounds in the azimuthal plane (i.e. their degree to the left or the right). There are two major cues to sound localization: Interaural level differences (ILD) and interaural time differences (ITD). The ILD measures differences in sound intensity between the ears. This works for high frequencies (over 1.6 kHz), where the wavelength is shorter than the distance between the ears, causing a head shadow - which means that high frequency sounds hit the averted ear with lower intensity. Lower frequency sounds don't cast a shadow, since they wrap around the head. However, due to the wavelength being larger than the distance between the ears, there is a phase difference between the sound waves entering the ears - the timing difference measured by the ITD. This works very precisely for frequencies below 800 Hz, where the ear distance is smaller than half of the wavelength. Sound localization in the median plane (front, above, back, below) is helped through the outer ear, which forms direction-selective filters.
There, the differences in time and loudness of the sound information in each ear are compared. Differences in sound intensity are processed in cells of the lateral superior olivary complexm and timing differences (runtime delays) in the medial superior olivary complex. Humans can detect timing differences between the left and right ear down to 10 μs, corresponding to a difference in sound location of about 1 deg. This comparison of sound information from both ears allows the determination of the direction where the sound came from. The superior olive is the first node where signals from both ears come together and can be compared. As a next step, the superior olivary complex sends information up to the inferior colliculus via a tract of axons called lateral lemniscus. The function of the inferior colliculus is to integrate information before sending it to the thalamus and the auditory cortex. It is interesting to know that the superior colliculus close by shows an interaction of auditory and visual stimuli.
- Dorsal Cochlear Nucleus:
The dorsal cochlear nucleus (DCN) analyzes the quality of sound and projects directly via the lateral lemnisucs to the inferior colliculus.
From the inferior colliculus the auditory information from ventral as well as dorsal cochlear nucleus proceeds to the auditory nucleus of the thalamus which is the medial geniculate nucleus. The medial geniculate nucleus further transfers information to the primary auditory cortex, the region of the human brain that is responsible for processing of auditory information, located on the temporal lobe. The primary auditory cortex is the first relay involved in the conscious perception of sound.
Primary auditory cortex and higher order auditory areas
[edit | edit source]Sound information that reaches the primary auditory cortex (Brodmann areas 41 and 42). The primary auditory cortex is the first relay involved in the conscious perception of sound. It is known to be tonotopically organized and performs the basics of hearing: pitch and volume. Depending on the nature of the sound (speech, music, noise), is further passed to higher order auditory areas. Sounds that are words are processed by Wernicke’s area (Brodmann area 22). This area is involved in understanding written and spoken language (verbal understanding). The production of sound (verbal expression) is linked to Broca’s area (Brodmann areas 44 and 45). The muscles to produce the required sound when speaking are contracted by the facial area of motor cortex which are regions of the cerebral cortex that are involved in planning, controlling and executing voluntary motor functions.

Pitch Perception
[edit | edit source]This section reviews a key topic in auditory neuroscience: pitch perception. Some basic understanding of the auditory system is presumed, so readers are encouraged to first read the above sections on the 'Anatomy of the Auditory System' and 'Auditory Signal Processing'.
Introduction
[edit | edit source]Pitch is a subjective percept, evoked by sounds that have an approximately periodic nature. For many naturally occurring sounds, periodicity of a sound is the major determinant of pitch. Yet the relationship between an acoustic stimulus and pitch is quite abstract: in particular, pitch is quite robust to changes in other acoustic parameters such as loudness or spectral timbre, both of which may significantly alter the physical properties of an acoustic waveform. This is particularly evident in cases where sounds without any shared spectral components can evoke the same pitch, for example. Consequently, pitch-related information must be extracted from spectral and/or temporal cues represented across multiple frequency channels.
Investigations of pitch encoding in the auditory system have largely focused on identifying neural processes which reflect these extraction processes, or on finding the ‘end point’ of such a process: an explicit, robust representation of pitch as perceived by the listener. Both endeavours have had some success, with evidence accumulating for ‘pitch selective neurons’ in putative ‘pitch areas’. However, it remains debatable whether the activity of these areas is truly related to pitch, or if they simply exhibit selective representation of pitch-related parameters. On the one hand, demonstrating an activation of specific neurons or neural areas in response to numerous pitch-evoking sounds, often with substantial variation in their physical characteristics, provides compelling correlative evidence that these regions are indeed encoding pitch. On the other, demonstrating causal evidence that these neurons represent pitch is difficult, likely requiring a combination of in vivo recording approaches to demonstrate a correspondence of these responses to pitch judgments (i.e., psychophysical responses, rather than just stimulus periodicity), and direct manipulation of the activity in these cells to demonstrate predictable biases or impairments in pitch perception.
Due to the rather abstract nature of pitch, we will not immediately delve into this yet unresolved field of active research. Rather, we begin our discussion with the most direct physical counterparts of pitch perception – i.e., sound frequency (for pure tones) and, more generally, stimulus periodicity. Specifically, we will distinguish between, and more concretely define, the notions of periodicity and pitch. Following this, we will briefly outline the major computational mechanisms that may be implemented by the auditory system to extract such pitch-related information from sound stimuli. Subsequently, we outline representation and processing of pitch parameters in the cochlea, the ascending subcortical auditory pathway, and, finally, more controversial findings in primary auditory cortex and beyond, and evaluate the evidence of ‘pitch neurons’ or ‘pitch areas’ in these cortical regions.
Periodicity and pitch
[edit | edit source]Pitch is an emergent psychophysical property. The salience and ‘height’ of pitch depends on several factors, but within a specific range of harmonic and fundamental frequencies, called the “existence region”, pitch salience is largely determined by regularity of sound segment repetition; pitch height by the rate of repetition, also called the modulating frequency. The set of sounds capable of evoking pitch perception is diverse and spectrally heterogeneous. Many different stimuli – including pure tones, click trains, iterated ripple noises, amplitude modulated sounds, and so forth – can evoke a pitch percept, while another acoustic signals, even with very similar physical characteristics to such stimuli may not evoke pitch. Most naturally occurring pitch-evoking sounds are harmonic complexes - sounds containing a spectrum of frequencies that are integer multiples of the fundamental frequency, F0. An important finding in pitch research is the phenomenon of the ‘missing fundamental’ (see below): within a certain frequency range, all the spectral energy at F0 can be removed from a harmonic complex, and still evoke a pitch correlating to F0 in a human listener[2]. This finding appears to generalise to many non-human auditory systems[3][4].

| Demo: Pitch of the missing fundamental
Melody played with only harmonic overtones, with spectral energy at the fundamental frequencies removed. fhead
|
|
| Problems listening to these files? See media help. | |
The ‘missing fundamental’ phenomenon is important for two reasons. Firstly, it is an important benchmark for assessing whether particular neurons or brain regions are specialised for pitch processing, since such units should be expected to show activity reflective of F0 (and thus pitch), regardless of its presence in the sound and other acoustic parameters. More generally, a ‘pitch neuron’ or ‘pitch centre’ should show consistent activity in response to all stimuli that evoke a particular perception of pitch height. As will be discussed, this has been a source of some disagreement in identifying putative pitch neurons or areas. Secondly, that we can perceive a pitch corresponding to F0 even in its absence in the auditory stimulus provides strong evidence against the brain implementing a mechanism for ‘selecting’ F0 to directly infer pitch. Rather, pitch must be extracted from temporal or spectral cues (or both)[5].
Mechanisms for pitch extraction: spectral and temporal cues
[edit | edit source]
These two cues (spectral and temporal) are the bases of two major classes of pitch extraction models[5]. The first of these are the time domain methods, which use temporal cues to assess whether a sound consists of a repetitive segment, and, if so, the rate of repetition. A commonly proposed method of doing so is autocorrelation. An autocorrelation function essentially involves finding the time delays between two sampling points that will give the maximum correlation: for example, a sound wave with a frequency of 100Hz (or period, T=10 milliseconds) would have a maximal correlation if samples are taken 10 milliseconds apart. For a 200Hz wave, the delay yielding maximal correlation would be 5 milliseconds – but also at 10 milliseconds, 15 milliseconds and so forth. Thus if such a function is performed on all component frequencies of a harmonic complex with F0=100Hz (and thus having harmonic overtones at 200Hz, 300Hz, 400Hz, and so forth), and the resulting time intervals giving maximal correlation were summed, they would collectively ‘vote’ for 10 milliseconds – the periodicity of the sound. The second class of pitch extraction strategies are frequency domain methods, where pitch is extracted by analysing the frequency spectra of a sound to calculate F0. For instance, ‘template matching' processes – such as the ‘harmonic sieve’ – propose that the frequency spectrum of a sound is simply matched to harmonic templates – the best match yields the correct F0[6].
There are limitations to both classes of explanations. Frequency domain methods require harmonic frequencies to be resolved – that is, for each harmonic to be represented as a distinct frequency band (see figure, right). Yet higher order harmonics, which are unresolved due to the wider bandwidth in physiological representation for higher frequencies (a consequence of the logarithmic tonotopic organisation of the basilar membrane), can still evoke pitch corresponding to F0. Temporal models do not have this issue, since an autocorrelation function should still yield the same periodicity, regardless of whether the function is performed in one or over several frequency channels. However, it is difficult to attribute the lower limits of pitch-evoking frequencies to autocorrelation: psychophysical studies demonstrate that we can perceive pitch from harmonic complexes with missing fundamentals as low as 30Hz; this corresponds to a sampling delay of over 33 milliseconds – far longer than the ~10 millisecond delay commonly observed in neural signalling[5].

One strategy to determine which of these two strategies are adopted by the auditory system is the use of alternating-phase harmonics: to present odd harmonics in sine phase, and even harmonics in cosine phase. Since this will not affect the spectral content of the stimulus, no change in pitch perception should occur if the listener is relying primarily on spectral cues. On the other hand, the temporal envelope repetition rate will double. Thus, if temporal envelope cues are adopted, the pitch perceived by listeners for alternating-phase harmonics will be an octave above (i.e., double the frequency of) the pitch perceived for all-cosine harmonic with the same spectral composition. Psychophysical studies have investigated the sensitivity of pitch perception to such phase shifts across different F0 and harmonic ranges, providing evidence that both humans[7] and other primates[8] adopt a dual strategy: spectral cues are used for lower order, resolved harmonics, while temporal envelope cues are used higher order, unresolved harmonics.
Pitch extraction in the ascending auditory pathway
[edit | edit source]Weber fractions for pitch discrimination in humans has been reported at under 1%[9]. In view of this high sensitivity to pitch changes, and the demonstration that both spectral and temporal cues are used for pitch extraction, we can predict that the auditory system represents both the spectral composition and temporal fine structure of acoustic stimuli in a highly precise manner, until these representations are eventually conveyed explicitly periodicity or pitch-selective neurons.
Electrophysiological experiments have identified neuronal responses in the ascending auditory system that are consistent with this notion. From the level of the cochlea, the tonopically mapped basilar membrane’s (BM) motions in response to auditory stimuli establishes a place code for frequency composition along the BM axis. These representations are further enhanced by a phase-locking of the auditory nerve fibres (ANFs) to the frequency components it responds to. This mechanism for temporal representation of frequency composition is further enhanced in numerous ways, such as lateral inhibition at the hair cell/spiral ganglion cell synapse[10], supporting the notion that this precise representation is critical for pitch encoding.
Thus by this stage, the phase-locked temporal spike patterns of ANFs likely carry an implicit representation of periodicity. This was tested directly by Cariani and Delgutte[11]. By analysing the distribution of all-order inter-spike intervals (ISI) in the ANFs of cats, they showed that the most common ISI was the periodicity of the stimulus, and the peak-to-mean ratio of these distribution increased for complex stimuli evoking more salient pitch perceptions. Based on these findings, these authors proposed the ‘predominant interval hypothesis’, where a pooled code of all-order ISIs ‘vote’ for the periodicity - though of course, this finding is an inevitable consequence of phase-locked responses of ANFs. In addition, there is evidence that the place code for frequency components is also critical. By crossing a low-frequency stimulus with a high-frequency carrier, Oxenham et al transposed the temporal fine-structure of the low frequency sinusoid to higher frequency regions along the BM.[12] This led to significantly impaired pitch discrimination abilities. Thus, both the place and temporal coding represent pitch-related information in the ANFs.
The auditory nerve carries information to the cochlear nucleus (CN). Here, many cell types represent pitch-related information in different ways. For example, many bushy cells appear to have little difference in firing properties of auditory nerve fibres – information may be carried to higher order brain regions without significant modification[5].Of particular interest are the sustained chopper cells in the ventral cochlear nucleus. According Winter and colleagues, the first-order spike intervals in these cells corresponds to periodicity in response to iterated rippled noise stimuli (IRN), as well to cosine-phase and random-phase harmonic complexes, quite invariantly to sound level[13]. While further characterisation of these cells' responses to different pitch-evoking stimuli is required, there is therefore some indication that pitch extraction may begin as early as the level of the CN.
In the inferior colliculus (IC), there is some evidence that the average response rate of neurons is equal to the periodicity of the stimulus[14]. Subsequent studies comparing IC neuron responses to same-phase and alternating-phase harmonic complexes suggest that these cells may be responding to the periodicity of the overall energy level (i.e., the envelope), rather than true modulating frequency, yet it is not clear whether this applies only for unresolved harmonics (as would be predicted by psychophysical experiments) or also for resolved harmonics[5]. There remains much uncertainty regarding the representation of periodicity in the IC.
Pitch coding in the auditory cortex
[edit | edit source]Thus, there is a tendency to enhance that representations of F0 throughout the ascending auditory system, though the precise nature of this remains unclear. In these subcortical stages of the ascending auditory pathway however, there is no evidence for an explicit representation that consistently encodes information corresponding to perceived pitch. Such representations likely occur in ‘higher’ auditory regions, from primary auditory cortex onward.
Indeed, lesion studies have demonstrated the necessity for auditory cortex in pitch perception. Of course, an impairment in pitch detection following lesions to the auditory cortex may simply be reflect a passive transmission role for the cortex: where subcortical information must ‘pass through’ to affect behaviour. Yet studies such as that by Whitfield have demonstrated that this is likely not the case: while decorticate cats could be re-trained (following an ablation of their auditory cortex) to recognise complex tones comprised of three frequency components, the animals selectively lost the ability generalise these tones to other complexes with the same pitch[15]. In other words, while the harmonic composition could influence behaviour, harmonic relations (i.e. a pitch cue) could not. For example, the lesioned animal could correctly respond to a pure tone at 100Hz, but would not respond to a harmonic complex consisting of its harmonic overtones (at 200Hz, 300Hz, and so forth). This suggests strongly a role for the auditory cortex in further extraction of pitch-related information.
Early MEG studies of the primary auditory cortex had suggested that A1 contained a map of pitch. This was based on the findings that a pure tone and its missing fundamental harmonic complex (MF) evoked stimulus-evoked excitation (called the N100m) in the same location, whereas components frequencies of the MF presented in isolation evoked excitations in different locations[16]. Yet such notions were overcast by the results of experiments using higher spatial-resolution techniques: local field potential (LFP) and multi-unit recording (MUA) demonstrated that the mapping A1 was tonotopic – that is, based on neurons’ best frequency (BF), rather than best ‘pitch’[17]. These techniques do however demonstrate an emergence of distinct coding mechanisms reflective of extracting temporal and spectral cues: phase-locked representation of temporal envelope repetition rate was recorded in the higher BF regions of the tonotopic map, while the harmonic structure of the click train was represented in lower BF regions[18].Thus, the cues for pitch extraction may be further enhanced by this stage.

An example of a neuronal substrate that may facilitate such an enhancement was described by Kadia and Wang in primary auditory cortex of marmosets[19]. Around 20% of the neurons here could be classified as ‘multi-peaked’ units: neurons that have multiple frequency response areas, often in harmonic relation (see figure, right). Further, excitation of two of these spectral peaks what shown to have a synergistic effect on the neurons’ responses. This would therefore facilitate the extraction of harmonically related tones in the acoustic stimulus, allowing these neurons to act as a ‘harmonic template’ for extracting spectral cues. Additionally, these authors observed that in the majority of ‘single peaked’ neurons (i.e. neurons with a single spectral tuning peak at its BF), a secondary tone could have a modulatory (facilitating or inhibiting) effect on the response of the neuron to its BF. Again, these modulating frequencies were often harmonically related to the BF. These facilitating mechanisms may therefore accommodate the extraction of certain harmonic components, while rejecting other spectral combinations through inhibitory modulation may facilitate the disambiguation with other harmonic complexes or non-harmonic complexes such as broadband noise.

However, given that the tendency to enhance F0 has been demonstrated throughout the subcortical auditory system, we might expect have to come closer to a more explicit representation of pitch in the cortex. Neuroimaging experiments have explored this idea, capitalising on the emergent quality of pitch: a subtractive method can identify areas in the brain which show BOLD responses in response to a pitch-evoking stimulus, but not to another sound with very similar spectral properties, but does not evoke pitch perception. Such strategies were used by Patterson, Griffiths and colleagues: by subtracting the BOLD signal acquired during presentation of broad-band noise from the signal acquired during presentation of IRN, they identified a selective activation of the lateral (and to some extent, medial) Heschl’s gyrus (HG) in response to the latter class of pitch-evoking sounds[20]. Further, varying the repetition rate of IRN over time to create a melody led to additional activation in the superior temporal gyrus (STG) and planum polare (PP), suggesting a hierarchical processing of pitch through the auditory cortex. In line with this, MEG recordings by Krumbholz et al showed that, as the repetition rate of IRN stimuli is increased, a novel N100m is detected around the HG as the repetition rate crosses the lower threshold for pitch perception, and the magnitude of this “pitch-onset response” increased with pitch salience[21].
There is however some debate about the precise location of the pitch selective area. As Hall and Plack point out, the use of IRN stimuli alone to identify pitch-sensitive cortical areas is insufficient to capture the broad range of stimuli that can induce pitch perception: the activation of HG may be specific to repetitive broadband stimuli[22]. Indeed, based on BOLD signals observed in response to multiple pitch-evoking stimuli, Hall and Plack suggest that the planum temporale (PT) is more relevant for pitch processing.
Despite ongoing disagreement about the precise neural area specialised for pitch coding, such evidence suggests that regions lying anterolateral to A1 may be specialised for pitch perception. Further support for this notion is provided by the identification of ‘pitch selective’ neurons at the anterolateral border of A1 in the marmoset auditory cortex. These neurons were selectively responsive to both pure tones and missing F0 harmonics with the similar periodicities[23]. Many of these neurons were also sensitive to the periodicity of other pitch-evoking stimuli, such as click trains or IRN noise. This provides strong evidence that these neurons are not merely responding any particular component of the acoustic signal, but specifically represent pitch-related information.
Periodicity coding or pitch coding?
[edit | edit source]Accumulating evidence thus suggests that there are neurons and neural areas specialised in extracting F0, likely in regions just anterolateral to the low BF regions of A1. However, there are still difficulties in calling these neurons or areas “pitch selective”. While stimulus F0 is certainly a key determinant of pitch, it is not necessarily equivalent to the pitch perceived by the listener.
There are however several lines of evidence suggesting that these regions are indeed coding pitch, rather than just F0. For instance, further investigation of the marmoset pitch-selective units by Bendor and colleagues has demonstrated that the activity in these neurons corresponds well to the animals' psychophysical responses[8]. These authors tested the animals’ abilities to detect an alternating-phase harmonic complex amidst an ongoing presentation of same-phase harmonics at the same F0, in order to distinguish between when animals rely more on temporal envelope cues for pitch perception, rather than spectral cues. Consistent with psychophysical experiments in humans, the marmosets used primarily temporal envelope cues for higher order, unresolved harmonics of low F0, while spectral cues were used to extract pitch from lower-order harmonics of high F0 complexes. Recording from these pitch selective neurons showed that the F0 tuning shifted down an octave for alternating-phase harmonics, compared to same-phase harmonics for neurons tuned to low F0s. These patterns of neuronal responses are thus consistent with the psychophysical results, and suggest that both temporal and spectral cues are integrated in these neurons to influence pitch perception.
Yet, again, this study cannot definitively distinguish whether these pitch-selective neurons explicitly represent pitch, or simply an integration of F0 information that will then be subsequently decoded to perceive pitch. A more direct approach to addressing this issue was taken by Bizley et al, who analysed how auditory cortex LFP and MUA measurements in ferrets could independently be used to estimate stimulus F0 and pitch perception[24]. While ferrets were engaged in a pitch discrimination task (to indicate whether a target artificial vowel sound was higher or lower in pitch than a reference in a 2-alternative forced choice paradigm), receiver operating characteristic (ROC) analysis was used to estimate the discriminability of neural activity in predicting the change in F0 or the actual behavioural choice (i.e. a surrogate for perceived pitch). They found that neural responses across the auditory cortex were informative regarding both. Initially, the activity better discriminated F0 than the animal’s choice, but information regarding the animals’ choice grew steadily higher throughout the post-stimulus interval, eventually becoming more discriminable than the direction of F0 change[24].
Comparing the differences in ROC between the cortical areas studied showed that posterior fields activity better discriminated the ferrets’ choice. This may be interpreted in two ways. Since choice-related activity was higher in the posterior fields (which lie by the low BF border of A1), compared to the primary fields, this may be seen as further evidence for pitch-selectivity near low BF border of A1. On the other hand, the fact the pitch-related information was also observed in the primary auditory fields may suggest that sufficient pitch-related information may already be established by this stage, or that a distributed code across multiple auditory areas code pitch. Indeed, while single neurons distributed across the auditory cortex are in general sensitive to multiple acoustic parameters (and therefore not ‘pitch-selective’), information theoretic or neurometric analyses (using neural data to infer stimulus-related information) indicate that pitch information can nevertheless be robustly represented via population coding, or even by single neurons through temporal multiplexing (i.e., representing multiple sound features in distinct time windows)[25][26]. Thus, in the absence of stimulation or deactivation of these putative pitch-selective neurons or areas to demonstrate that such interventions induce predictable biases or impairments in pitch, it may be that pitch is represented in spatially and temporally distributed codes across the auditory cortex, rather than relying on specialised local representations.
Thus, both electrophysiological recording and neuroimaging studies suggest that there may be an explicit neural code for pitch lies near the low BF border of A1. Certainly, the consistent and selective responses to a wide range of pitch-evoking stimuli suggest that these putative pitch-selective neurons and areas are not simply reflecting any immediately available physical characteristic of the acoustic signal. Moreover, there is evidence that these putative pitch-selective neurons extract information from spectral and temporal cues in much the same way as the animal. However, by virtue of the abstract relationship between pitch and an acoustic signal, such correlative evidence between a stimulus and neural response can only be interpreted as evidence that the auditory system has the capacity to form enhanced representations of pitch-related parameters. Without more direct causal evidence for these putative pitch-selective neurons and neural areas determining pitch perception, we cannot conclude whether animals do indeed rely on such localised explicit codes for pitch, or if the robust distributed representations of pitch across the auditory cortex mark the final coding of pitch in the auditory system.
References
[edit | edit source]- ↑ NeurOreille and authors (2010). "Journey into the world of hearing".
- ↑ Schouten, J. F. (1938). The perception of subjective tones. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 41, 1086-1093.
- ↑ Cynx, J. & Shapiro, M. Perception of missing fundamental by a species of songbird (Sturnus vulgaris). J Comp Psychol 100, 356–360 (1986).
- ↑ Heffner, H., & Whitfield, I. C. (1976). Perception of the missing fundamental by cats. The Journal of the Acoustical Society of America, 59(4), 915-919.
- ↑ a b c d e Schnupp, J., Nelken, I. & King, A. Auditory neuroscience: Making sense of sound. (MIT press, 2011).
- ↑ Gerlach, S., Bitzer, J., Goetze, S. & Doclo, S. Joint estimation of pitch and direction of arrival: improving robustness and accuracy for multi-speaker scenarios. EURASIP Journal on Audio, Speech, and Music Processing 2014, 1 (2014).
- ↑ Carlyon RP, Shackleton TM (1994). "Comparing the fundamental frequencies of resolved and unresolved harmonics: Evidence for two pitch mechanisms?" Journal of the Acoustical Society of America 95:3541-3554
- ↑ a b Bendor D, Osmanski MS, Wang X (2012). "Dual-pitch processing mechanisms in primate auditory cortex," Journal of Neuroscience 32:16149-61.
- ↑ Tramo, M. J., Shah, G. D., & Braida, L. D. (2002). Functional role of auditory cortex in frequency processing and pitch perception. Journal of Neurophysiology, 87(1), 122-139.
- ↑ Rask-Andersen, H., Tylstedt, S., Kinnefors, A., & Illing, R. B. (2000). Synapses on human spiral ganglion cells: a transmission electron microscopy and immunohistochemical study. Hearing research, 141(1), 1-11.
- ↑ Cariani, P. A., & Delgutte, B. (1996). Neural correlates of the pitch of complex tones. I. Pitch and pitch salience. Journal of Neurophysiology, 76(3), 1698-1716.
- ↑ Oxenham, A. J., Bernstein, J. G., & Penagos, H. (2004). Correct tonotopic representation is necessary for complex pitch perception. Proceedings of the National Academy of Sciences of the United States of America, 101(5), 1421-1425.
- ↑ Winter, I. M., Wiegrebe, L., & Patterson, R. D. (2001). The temporal representation of the delay of iterated rippled noise in the ventral cochlear nucleus of the guinea-pig. The Journal of physiology, 537(2), 553-566.
- ↑ Schreiner, C. E. & Langner, G. Periodicity coding in the inferior colliculus of the cat. II. Topographical organization. Journal of neurophysiology 60, 1823–1840 (1988).
- ↑ Whitfield IC (1980). "Auditory cortex and the pitch of complex tones." J Acoust Soc Am. 67(2):644-7.
- ↑ Pantev, C., Hoke, M., Lutkenhoner, B., & Lehnertz, K. (1989). Tonotopic organization of the auditory cortex: pitch versus frequency representation.Science, 246(4929), 486-488.
- ↑ Fishman YI, Reser DH, Arezzo JC, Steinschneider M (1998). "Pitch vs. spectral encoding of harmonic complex tones in primary auditory cortex of the awake monkey," Brain Res 786:18-30.
- ↑ Steinschneider M, Reser DH, Fishman YI, Schroeder CE, Arezzo JC (1998) Click train encoding in primary auditory cortex of the awake monkey: evidence for two mechanisms subserving pitch perception. J Acoust Soc Am 104:2935–2955.
- ↑ Kadia, S. C., & Wang, X. (2003). Spectral integration in A1 of awake primates: neurons with single-and multipeaked tuning characteristics. Journal of neurophysiology, 89(3), 1603-1622.
- ↑ Patterson RD, Uppenkamp S, Johnsrude IS, Griffiths TD. (2002) "The processing of temporal pitch and melody information in auditory cortex," Neuron 36:767-776.
- ↑ Krumbholz, K., Patterson, R. D., Seither-Preisler, A., Lammertmann, C., & Lütkenhöner, B. (2003). Neuromagnetic evidence for a pitch processing center in Heschl’s gyrus. Cerebral Cortex, 13(7), 765-772.
- ↑ Hall DA, Plack CJ (2009). "Pitch processing sites in the human auditory brain," Cereb Cortex 19(3):576-85.
- ↑ Bendor D, Wang X (2005). "The neuronal representation of pitch in primate auditory cortex," Nature 436(7054):1161-5.
- ↑ a b Bizley JK, Walker KMM, Nodal FR, King AJ, Schnupp JWH (2012). "Auditory Cortex Represents Both Pitch Judgments and the Corresponding Acoustic Cues," Current Biology 23:620-625.
- ↑ Walker KMM, Bizley JK, King AJ, and Schnupp JWH. (2011). Multiplexed and robust representations of sound features in auditory cortex. Journal of Neurosci 31(41): 14565-76
- ↑ Bizley JK, Walker KM, King AJ, and Schnupp JW. (2010). "Neural ensemble codes for stimulus periodicity in auditory cortex." J Neurosci 30(14): 5078-91.


