Probability/Random Variables

Random variable

Motivation

In many experiments, there may be so many possible outcomes in the sample space that we may want to instead work with a "summary variable" for those outcomes. For example, suppose a poll is conducted for 100 different people to ask them whether they agree with a certain proposal. Then, to keep track of the answers from those 100 people completely, we may first use a number to indicate the response:

• number "1" for "agree".
• number "0" for "disagree".

(For simplicity, we assume that there are only these two responses available.) After that, to record which person answer which response, we use a vector with 100 numbers for the record. For example, $(1,0,1,0,0,\dotsc ,1,0,0)$, etc. Since for every coordinate in the vector, there are two choices: "0" or "1", there are in total $2^{100}\approx 1.268\times 10^{30}$ different vectors in the sample space (denoted by $\Omega$)! Hence, it is very tedious and complicated to work with that many outcomes in the sample space $\Omega$. Instead, we are often only interested in how many "agree" and "disagree" are there, instead of which person answers which response, since the number of "agree" and "disagree" determines whether the proposal is agreed by majority of them, and thus captures the essence of the poll.

Hence, it is more convenient to define a variable $X$ which gives the number of "1"s in the 100 coordinates in every outcome in the sample space $\Omega$. Then, $X$ can only take 101 possible values: 0,1,2,...,100, which is much fewer than the number of outcomes in the original sample space.

Through this, we can change the original experiment to a new experiment, where the variable $X$ takes one of the 101 possible values according to certain probabilities. For this new experiment, the sample space becomes $\{0,1,\dotsc ,100\}$.

During the above process of defining the variable $X$ (called random variable), we have actually (implicitly) defined a function where the domain is the original sample space, and the range is $\{0,1,\dotsc ,100\}$. Usually, we take the codomain of the random variable to be the set of all real numbers $\mathbb {R}$. That is, we define the random variable $X:\Omega \to \mathbb {R}$ by

$$X(\omega )={\text{number of 1s in the coordinates of }}\omega$$

for every $\omega \in \Omega$.

Definition

To define random variable formally, we need the concept of measurable function:

Definition. (Measurable function) Let $(A,\Sigma _{1})$ and $(B,\Sigma _{2})$ be measurable spaces (that is, $\Sigma _{1}$ and $\Sigma _{2}$ are $\sigma$-algebras of $A$ and $B$ respectively). A function $f:A\to B$ is ($\Sigma _{1}$-)measurable if for every $Y\in \Sigma _{2}$, the pre-image of $Y$ under $f$

$$f^{-1}(Y)=\{x\in A:f(x)\in Y\}\in \Sigma _{1}.$$

Remark.

• If $f:A\to B$ is $\Sigma _{1}$-measurable, then we may also write $f:(A,\Sigma _{1})\to (B,\Sigma _{2})$ to emphasize the dependency on the $\sigma$-algebras $\Sigma _{1}$ and $\Sigma _{2}$.
• We just consider the pre-image of set $Y$ in the $\sigma$-algebra $\Sigma _{2}$ since only the sets in $\Sigma _{2}$ are "well-behaved", and hence they are "of interest". Then, the measurability of $f$ ensures that the pre-image is also "well-behaved".

• So, a measurable function preserves the "well-behavedness" of a set in some sense.
• It also turns out that using pre-image (instead of image) in the definition is more useful.

Definition. (Random variable)

A graphical illustration of random variable.

Let $(\Omega ,{\mathcal {F}},\mathbb {P} )$ be a probability space. A random variable is a ${\mathcal {F}}$-measurable function $X:(\Omega ,{\mathcal {F}})\to (\mathbb {R} ,{\mathcal {B}})$.

Remark.

• Usually, a capital letter is used to represent a random variable, and the small corresponding letter is used to represent the realized value (i.e., the numerical value mapped from a sample point) of the random variable. For example, we say that a realized value of the random variable $X$ is $x$.
• The $\sigma$-algebra ${\mathcal {B}}$ is the Borel $\sigma$-algebra on $\mathbb {R}$. We will not discuss its definition in details here.
• Since $X$ is ${\mathcal {F}}$-measurable, we have for every set $B\in {\mathcal {B}}$, the pre-image $X^{-1}(B)=\{\omega :X(\omega )\in B\}\in {\mathcal {F}}$.

• It is common to use $\{X\in B\}$ to denote $X^{-1}(B)$. Furthermore, we use $\{X\leq x\},\{X=x\}$, etc. to denote $X^{-1}((-\infty ,x]),X^{-1}(\{x\})$, etc.

• We require the random variable to be ${\mathcal {F}}$-measurable, so that the probability $\mathbb {P} (\{X\in B\})$ (often written $\mathbb {P} (X\in B)$ instead) is defined for every $B\in {\mathcal {B}}$. (The domain of probability measure is ${\mathcal {F}}$, and $\{X\in B\}\in {\mathcal {F}}$ because of the ${\mathcal {F}}$-measurability of the random variable $X$.)
• Generally, most functions (that are supposed to be random variables) we can think of are ${\mathcal {F}}$-measurable. Hence, we will just assume without proof that the random variables constructed here are ${\mathcal {F}}$-measurable, and thus are actually valid.

By defining a random variable $X:\Omega \to \mathbb {R}$ from a probability space $(\Omega ,{\mathcal {F}},\mathbb {P} )$, we actually induce a new probability space $({\mathcal {X}},{\mathcal {F}}_{X},\mathbb {P} _{X})$ where

• The induced sample space ${\mathcal {X}}$ is the range of the random variable $X$: ${\mathcal {X}}=\{X(\omega ):\omega \in \Omega \}\subseteq \mathbb {R}$.
• The induced event space ${\mathcal {F}}_{X}$ is a $\sigma$-algebra of ${\mathcal {X}}$. (Here, we follow our previous convention: ${\mathcal {F}}_{X}={\mathcal {P}}({\mathcal {X}})$ when ${\mathcal {X}}$ is countable.)
• The induced probability measure $\mathbb {P} _{X}:{\mathcal {F}}_{X}\to [0,1]$ is defined by

$$\mathbb {P} _{X}(E)=\mathbb {P} (\{X\in E\})$$

for every $E\in {\mathcal {F}}_{X}$.

It turns out the induced probability measure satisfies all the probability axioms:

Example. Prove that the induced probability measure $\mathbb {P} _{X}$ satisfies all the probability axioms, and hence is valid.

Proof. Nonnegativity: For every event $E\in {\mathcal {F}}_{X}$,

$$\mathbb {P} _{X}(E)=\underbrace {\mathbb {P} (\{X\in E\})\geq 0} _{{\text{nonnegativity of }}\mathbb {P} }.$$

Unitarity: We have

$$\mathbb {P} _{X}({\mathcal {X}})=\mathbb {P} (\{\omega \in \Omega :\underbrace {X(\omega )\in {\mathcal {X}}} _{\text{always true}}\})=\underbrace {\mathbb {P} (\Omega )=1} _{{\text{unitarity of }}\mathbb {P} }.$$

Particularly, we always have $X(\omega )\in {\mathcal {X}}$ for every $\omega \in \Omega$ by the construction of ${\mathcal {X}}$ (${\mathcal {X}}$ is the range of the random variable $X$).

Countable additivity: For every infinite sequence of pairwise disjoint events $E_{1},E_{2},\dotsc$ (every event involved belongs to ${\mathcal {F}}_{X}$),

$${\begin{aligned}\mathbb {P} \left(\bigcup _{i=1}^{\infty }E_{i}\right)&=\mathbb {P} \left(\left\{\omega \in \Omega :X(\omega )\in \bigcup _{i=1}^{\infty }E_{i}\right\}\right)\\&=\mathbb {P} \left(\bigcup _{i=1}^{\infty }\left\{\omega \in \Omega :X(\omega )\in E_{i}\right\}\right)\\&=\mathbb {P} \left({\color {blue}\bigcup _{i=1}^{\infty }}\bigcup _{x_{j}\in E_{i}}\left\{\omega \in \Omega :X(\omega )=x_{j}\right\}\right)\\&={\color {blue}\sum _{i=1}^{\infty }}\mathbb {P} \left(\bigcup _{x_{j}\in E_{i}}\left\{\omega \in \Omega :X(\omega )=x_{j}\right\}\right)&({\text{countable additivity of }}\mathbb {P} )\\&=\sum _{i=1}^{\infty }\mathbb {P} \left(\left\{\omega \in \Omega :X(\omega )\in E_{i}\right\}\right)\\&=\sum _{i=1}^{\infty }\mathbb {P} _{X}(E_{i}).\\\end{aligned}}$$

$\Box$

After proving this result, it follows that all properties of probability measure discussed previously also apply to the induced probability measure $\mathbb {P} _{X}$. Hence, we can use the properties of probability measure to calculate the probability $\mathbb {P} _{X}(E)$, and hence $\mathbb {P} (X\in E)$, for every set $E\in {\mathcal {F}}_{X}$. More generally, to calculate the probability $\mathbb {P} (X\in B)$ for every $B\in {\mathcal {B}}$ ($B$ does not necessarily belong to ${\mathcal {F}}_{X}$), we notice that $\{X\in B\}=\{X\in B\cap {\mathcal {X}}\}$, and it turns out that $B\cap {\mathcal {X}}\in {\mathcal {F}}_{X}$. Hence, we can calculate $\mathbb {P} (X\in B)$ by considering $\mathbb {P} _{X}(B\cap {\mathcal {X}})$.

Example. Suppose we toss a fair coin twice. Then, the sample space can be expressed by $\{{\text{HH, HT, TH, TT}}\}$. Now, we define the random variable $X$ to be the number of heads obtained in the tosses of a sample point (this means $X$ maps every sample point in the sample space to the number of heads obtained in that sample point). Then, we have

$${\begin{array}{ccccc}\omega &{\text{HH}}&{\text{HT}}&{\text{TH}}&{\text{TT}}\\\hline X(\omega )&2&1&1&0\\\end{array}}$$

Thus, $\{X=0\}=\{{\text{TT}}\},\{X=1\}=\{{\text{HT}},{\text{TH}}\},\{X=2\}=\{{\text{HH}}\}$. Hence, we have

$${\begin{array}{cccc}x&0&1&2\\\hline \mathbb {P} (X=x)&{\frac {1}{4}}&{\frac {2}{4}}&{\frac {1}{4}}\\\end{array}}$$

(The four outcomes in the sample space should be equally likely.) (It is common to write $\mathbb {P} (X=x)$ instead of $\mathbb {P} (\{X=x\})$, $\mathbb {P} (X\leq x)$ instead of $\mathbb {P} (\{X\leq x\})$, etc.)

Exercise. Suppose we toss a fair coin three times, and define the random variable $X$ to be the number of heads obtained in the tosses of a sample point. Then, ${\mathcal {X}}=\{0,1,2,3\}$. Calculate the probability $\mathbb {P} (X=x)$ for every $x\in {\mathcal {X}}$. Hence, calculate the probability $\mathbb {P} (X\leq x)$ for every $x\in {\mathcal {X}}$. (Hint: We can write $\mathbb {P} (X\leq x)=\mathbb {P} (X\in (-\infty ,x])$. Now, consider $\mathbb {P} _{X}((-\infty ,x]\cap {\mathcal {X}})$.)

Solution

First, we have

$${\begin{array}{ccccc}\omega &{\text{HHH}}&{\text{HHT}}&{\text{HTH}}&{\text{THH}}&{\text{TTH}}&{\text{THT}}&{\text{HTT}}&{\text{TTT}}\\\hline X(\omega )&3&2&2&2&1&1&1&0\\\end{array}}$$

It follows that we have

$${\begin{array}{cccc}x&0&1&2&3\\\hline \mathbb {P} (X=x)&{\frac {1}{8}}&{\frac {3}{8}}&{\frac {3}{8}}&{\frac {1}{8}}\\\end{array}}$$

Since $\mathbb {P} (X\leq x)=\mathbb {P} _{X}((-\infty ,x]\cap {\mathcal {X}})=\mathbb {P} _{X}(\{0,1,\dotsc ,x\})=\sum _{y=0}^{x}\mathbb {P} _{X}(\{y\})=\sum _{y=0}^{x}\mathbb {P} (X=y)$, it follows that we have

$${\begin{array}{cccc}x&0&1&2&3\\\hline \mathbb {P} (X\leq x)&{\frac {1}{8}}&{\frac {4}{8}}&{\frac {7}{8}}&{\frac {8}{8}}\\\end{array}}$$

Sometimes, even it is infeasible to list out all sample points in the sample space, we can also determine the probability related to the random variable.

Example. Consider the example about the poll discussed in the motivation part. We define the random variable to give the number of "1"s. Here, we assume that every sample point in the sample space is equally likely. Show that $\mathbb {P} (X=x)={\frac {\binom {100}{x}}{2^{100}}}$ for every $x\in {\mathcal {X}}=\{0,1,2,\dotsc ,100\}$.

Proof. Since there are ${\binom {100}{x}}$ sample points that contains $x$ "1"s (regard this as placing $x$ indistingusihable "1"s into 100 distinguishable cells), the result follows.

$\Box$

Remark.

• For example, $\mathbb {P} (X=3)\approx 1.276\times 10^{-25}$, $\mathbb {P} (X=50)\approx 0.07958924$, and $\mathbb {P} (X=79)\approx 1.6107\times 10^{-9}$.
• Plot of the values of $\mathbb {P} (X=x)$ for different values of $x$:

A special kind of random variable that is quite useful is the indicator random variable, which is a special case of indicator function:

Definition. (Indicator function)

A graphical illustration of indicator function. The "raised portion" is the set $A$, and the whole red square is the set $X$.

The indicator function of a subset $A$ of a set $X$ is a function $\mathbf {1} _{A}:X\to \{0,1\}$ defined by

$$\mathbf {1} _{A}(x)={\begin{cases}1&{\text{if }}x\in A\\0&{\text{if }}x\in X\setminus A.\end{cases}}$$

Remark.

• Special case: we can regard the indicator function as a random variable by modifying it a little bit:

• Let $(\Omega ,{\mathcal {F}},\mathbb {P} )$ be a probability space, and $A\in {\mathcal {F}}$ be an event. Then, the indicator random variable of the event $A$ is $\mathbf {1} _{A}:\Omega \to \mathbb {R}$ (here, we change the codomain to $\mathbb {R}$ to match with the definition of random variable) defined by

$$\mathbf {1} _{A}(\omega )={\begin{cases}1&{\text{if }}\omega \in A\\0&{\text{if }}\omega \in \Omega \setminus A.\end{cases}}$$

Example. Suppose we randomly select a citizen from a certain city, and record the annual income $\omega$ (in the currency used for that city) of that citizen. In this case, we can define the sample space as $\Omega =[0,\infty )$. Assume that the city has a taxation policy such that the annual income is taxable if it exceeds 10000 (in the same currency as $\omega$). Now, we let $X$ be the taxable income of the recorded annual income. To be more precise, $X:\Omega \to \mathbb {R}$ is defined by

$$X(\omega )={\begin{cases}0,&{\text{if }}\omega \leq 10000\\\omega -10000,&{\text{if }}\omega >10000.\end{cases}}$$

for every $\omega \in \Omega$. That is, $X(\omega )=\max\{\omega -c,0\}$, denoted by $(\omega -c)_{+}$, for every $\omega \in \Omega$.

Example. Suppose we roll two distinguishable dice, and define $X$ to be the sum of the numbers obtained in a outcome from the roll. Then, the sample space is $\Omega =\{(1,1),(1,2),\dotsc ,(6,6)\}$. Here, we can see that the range of $X$ is ${\mathcal {X}}=\{\underbrace {2} _{1+1},3,4,\dotsc ,\underbrace {12} _{6+6}\}$. Calculate $\mathbb {P} (X=x)$ for every $x\in {\mathcal {X}}$.

Solution. Notice that there are 1,2,3,4,5,6,5,4,3,2,1 sample points in the sample space where $X=2,3,\dotsc ,12$ respectively. Thus, we have

$${\begin{aligned}\mathbb {P} (X=2)&={\frac {1}{36}}\\\mathbb {P} (X=3)&={\frac {2}{36}}\\\mathbb {P} (X=4)&={\frac {3}{36}}\\\mathbb {P} (X=5)&={\frac {4}{36}}\\\mathbb {P} (X=6)&={\frac {5}{36}}\\\mathbb {P} (X=7)&={\frac {6}{36}}\\\mathbb {P} (X=8)&={\frac {5}{36}}\\\mathbb {P} (X=9)&={\frac {4}{36}}\\\mathbb {P} (X=10)&={\frac {3}{36}}\\\mathbb {P} (X=11)&={\frac {2}{36}}\\\mathbb {P} (X=12)&={\frac {1}{36}}.\\\end{aligned}}$$

Exercise. Calculate the probability that $\mathbb {P} (X\geq 8)$. (Answer: ${\frac {5}{12}}$)

Solution

The probability is

$$\mathbb {P} (X\geq 8)=\mathbb {P} _{X}(\{8,9,10,11,12\})=\sum _{x=8}^{12}\mathbb {P} _{X}(\{x\})=\sum _{x=8}^{12}\mathbb {P} (X=x)={\frac {5+4+3+2+1}{36}}={\frac {5}{12}}.$$

Cumulative distribution function

For every random variable $X$, there is function associating with it, called the cumulative distribution function (cdf) of $X$:

Definition.

Three examples of cdf, which are illustrated by the red lines and dots between two blue lines.

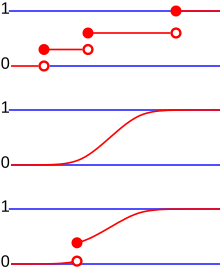
(Cumulative distribution function) The cumulative distribution function (cdf) of a random variable $X$, denoted by $F_{X}(x)$ (or $F(x)$) is

$$F_{X}(x)=\mathbb {P} (X\leq x)$$

for every $x\in \mathbb {R}$.

Example. Consider a previous exercise where we toss a fair coin three times, and the random variable $X$ is defined to be the number of heads obtained in the tosses of a sample point. We have calculated $\mathbb {P} (X\leq 0)={\frac {1}{8}},\quad \mathbb {P} (X\leq 1)={\frac {4}{8}},\quad \mathbb {P} (X\leq 2)={\frac {7}{8}},\quad \mathbb {P} (X\leq 3)={\frac {8}{8}}$. So, the cdf of the random variable $X$ is given by

$$F_{X}(x)={\begin{cases}0,&{\text{if }}x<0\\{\frac {1}{8}},&{\text{if }}0\leq x<1\\{\frac {4}{8}},&{\text{if }}1\leq x<2\\{\frac {7}{8}},&{\text{if }}2\leq x<3\\{\frac {8}{8}},&{\text{if }}x\geq 3.\\\end{cases}}$$

Graphically, the cdf is a step function with a jump for every $x\in {\mathcal {X}}=\{0,1,2,3\}$, where the size of the jump is $\mathbb {P} (X=x)$.

An illustration of the "jumps" in the cdf.

We can see from the cdf in the example above that the cdf is not necessarily continuous. There are several discontinuities at the jump points. But we can notice that at each jump point the cdf takes the value at the top of the jump, by the definition of cdf (the inequality involved includes also the equality). Loosely speaking, this suggests that the cdf is right-continuous. However, the cdf is not left-continuous in general.

In the following, we will discuss three defining properties of cdf.

Theorem. (Defining properties of cdf) A function $F$ is the cdf of a random variable $X$ if and only if

(i) $0\leq F(x)\leq 1$ for each real number $x$.

(ii) $F$ is nondecreasing.

(iii) $F$ is right-continuous.

Proof. Only if part ($F$ is cdf $\Rightarrow$ these three properties):

(i) It follows the axioms of probability since $F$ is defined to be a probability.

(ii)

$${\begin{aligned}x\leq y&\Rightarrow \{X\leq x\}\subseteq \{X\leq y\}\\&\Rightarrow \mathbb {P} (X\leq x)\leq \mathbb {P} (X\leq y)&\qquad {\text{by monotonicity}}\\&\Rightarrow F(x)\leq F(y)&\qquad {\text{by definition}}\\\end{aligned}}$$

(iii) Fix an arbitrary positive sequence $\epsilon _{1}>\epsilon _{2}>\cdots$ with $\lim _{n\to \infty }\epsilon _{n}=0$. Define $E_{n}=\{X\leq x+\epsilon _{n}\}$ for each positive number $n$. It follows that $E_{1}\supset E_{2}\supset \cdots$. Then,

$$\mathbb {P} (X\leq x)=\mathbb {P} \underbrace {\left(\lim _{n\to \infty }E_{n}\right)} _{\{X\leq x+0\}}=\mathbb {P} \left(\lim _{n\to \infty }E_{1}\cap E_{2}\cap \cdots E_{n}\right)=\lim _{n\to \infty }\mathbb {P} (E_{1}\cap \cdots \cap E_{n})=\lim _{n\to \infty }\mathbb {P} (E_{n})=\lim _{n\to \infty }\mathbb {P} (X\leq x+\epsilon _{n})$$

It follows that

$$F(x)=\lim _{n\to \infty }F(x+\epsilon _{n})$$

for each $\epsilon _{1}>\epsilon _{2}>\cdots$ with $\epsilon _{n}\to 0$ as $n\to \infty$. That is,

$$\lim _{h\to 0^{+}}F(x+h)=F(x)$$

which is the definition of right-continuity.

If part is more complicated. The following is optional. Outline:

1. Draw an arbitrary curve satisfying the three properties.
2. Throw a fair coin infinitely many times.
3. Encode each result into a binary number, e.g. $HHT\cdots \to 0.110\ldots$
4. Transform each binary number to a decimal number, e.g. $0.110\ldots \to 1(2^{-1})+1(2^{-2})=0.75\ldots$. Then, the decimal number is a random variable $U\in [0,1]$.
5. Use this decimal number as the input of the inverse function of the arbitrarily drawn curve, and we get a value, which is also a random variable, say $X$.
6. Then, we obtain a cdf of the random variable $X$ $F(x)=\mathbb {P} (X\leq x)=\mathbb {P} (U\leq F(x))$, if we throw a fair coin infinitely many times.

$\Box$

Sometimes, we are only interested in the values $x$ such that $\mathbb {P} (X=x)\neq 0$, which are more 'important'. Roughly speaking, the values are actually the elements of the support of $X$, which is defined in the following.

Definition. (Support of random variable) The support of a random variable $X$, $\operatorname {supp} (X)$, is the smallest closed set $S$ such that $\mathbb {P} (X\in S)=1$.

Remark.

• E.g. closed interval is closed set.
• Closedness will not be emphasized in this book.
• Practically, $\operatorname {supp} (X)=\{x\in \mathbb {R} :f(x)>0\}$ (which is the smallest closed set).

• $f(x)$ is probability mass function for discrete random variables;
• $f(x)$ is probability density function for continuous random variables.
• The terms mentioned above will be defined later.

Example. If

$$\mathbb {P} (X=x)={\begin{cases}1/4,\quad &x=0;\\1/8,\quad &x=3;\\5/8,\quad &x=6;\\0&{\text{otherwise}},\\\end{cases}}$$

then $\operatorname {supp} (X)=\{0,3,6\}$, since $\mathbb {P} (X\in \{0,3,6\})=1$ and this set is the smallest set among all sets satisfying this requirement.

Remark. $\mathbb {R} ,\{0,1,2,3,4,5,6\},$ etc. also satisfy the requirement, but they are not the smallest set.

Exercise.

Suppose we throw an unfair coin. Define $X=1$ if head comes up and $X=-1$ otherwise. Let $F(x)$ be the cdf of $X$.

1 Find $\operatorname {supp} (\mathbf {1} \{X=1\})$.

	$\{-1,1\}$
	$\{0,1\}$
	$\{\mathbf {1} \{X=1\}=0,\mathbf {1} \{X=1\}=1\}$
	It cannot be determined since the probability that head comes up is not given.

2 Suppose $\mathbb {P} (X=1)=0.7$, compute $F(0)$.

	0
	0.3
	0.5
	0.7
	1

3 Suppose $\mathbb {P} (X=1)=p\in (0,1)$. Which of the following is (are) true?

	$F(1)=1$
	$F(-1)=0$
	$F(0)+F(-1)=F(1)$
	$F(1)=2F(0.5)$ if the coin is fair instead.
	$\lim _{x\to -1^{-}}F(x)=F(-1)$

Discrete random variables

Definition. (Discrete random variables) If $\operatorname {supp} (X)$ is countable (i.e. 'enumerable' or 'listable'), then the random variable $X$ is a discrete random variable.

Example. Let $X$ be the number of successes among $n$ Bernoulli trials. Then, $X$ is a discrete random variable, since $\operatorname {supp} (X)=\{0,1,\ldots ,n\}$ which is countable.

On the other hand, if we let $Y$ be the temperature on Celsius scale, $Y$ is not discrete, since $\operatorname {supp} (Y)=[\underbrace {-273.15} _{\text{absolute zero}},\underbrace {1.417\times 10^{32}} _{\text{Planck temperature}}]$ which is not countable.

Exercise.

Which of the following is (are) discrete random variable?

	Number of heads coming up from tossing a coin three times.
	A number lying between 0 and 1 inclusively.
	Number of correct option(s) in a multiple choice question in which there are at most three correct options.
	Answer to a short question asking for a numeric answer.
	Probability for a random variable to be discrete random variable.

Often, for discrete random variable, we are interested in the probability that the random variable takes a specific value. So, we have a function that gives the corresponding probability for each specific value taken, namely probability mass function.

Definition.

An example of pmf. This function is called probability mass function, since the value at each point may be interpreted as the mass of the dot located at that point.

(Probability mass function) Let $X$ be a discrete random variable. The probability mass function (pmf) of $X$ is

$$f({\color {green}x})=\mathbb {P} (X={\color {green}x}).$$

Remark.

• Alternative names include mass function and probability function.
• If random variable $X$ is discrete, then $\operatorname {supp} (X)=\{x\in \mathbb {R} :f(x)>0\}$ (it is closed).
• The cdf of random variable $X$ is $F(x)=\mathbb {P} (X\leq x)=\sum _{\{y:y\leq x\}}f(y)$. It follows that the sum of the value of pmf at each $x$ inside the support equals one.
• The cdf of a discrete random variable $X$ is a step function with jumps at the points in $\operatorname {supp} (X)$, and the size of each jump defines the pmf of $X$ at the corresponding point in $\operatorname {supp} (X)$.

Example. Suppose we throw a fair six-faced dice one time. Let $X$ be the number facing up. Then, pmf of $X$ is

$$f(x)={\begin{cases}1/6,\quad &x=1,2,3,4,5{\text{ or }}6;\\0&{\text{otherwise}}.\end{cases}}$$

Exercise.

1 Which of the following is (are) pmf?

	$f(x)={\begin{cases}1/2^{n},\quad &n\in \mathbb {N} \\0&{\text{otherwise}}\end{cases}}$. It is given that $\mathbb {N} =\{1,2,\ldots \}$ is countable.
	$f(x)={\begin{cases}1,\quad &0\leq x\leq 1\\0&{\text{otherwise}}\end{cases}}$
	$f(x)={\begin{cases}0.2,\quad &x=2\\0.3,\quad &x=6\\0.4,\quad &x=8\\0&{\text{otherwise}}\end{cases}}$
	$f(x)={\begin{cases}0.2,\quad &x=2\\0.3,\quad &x=6\\0.4,\quad &x=8\\0.1&{\text{otherwise}}\end{cases}}$
	$f(x)={\frac {\mathbf {1} \{x=2\cup x=3\cup x=4\}}{3}}$

2 Compute $k$ such that the function $f(x)=\mathbf {1} \{x=k\}k+2(\mathbf {1} \{x=2k\}k)+3(\mathbf {1} \{x=3k\}k)$ is a pmf.

	$1/12$
	$1/6$
	$1/3$
	$1$

Continuous random variables

Suppose $X$ is a discrete random variable. Partitioning $S$ into small disjoint intervals $[x_{1},x_{1}+\Delta x_{1}],\dotsc$ gives

$$\mathbb {P} (X\in S)=\mathbb {P} \left(X\in \bigcup _{i}[x_{i}+\Delta x_{i}]\right)=\sum _{i}\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}=\sum _{i}\underbrace {\frac {\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}}{\Delta x_{i}}} _{\text{probability per unit}}\cdot \Delta x_{i}.$$

In particular, the probability per unit can be interpreted as the density of the probability of $X$ over the interval. (The higher the density, the more probability is distributed (or allocated) to that interval).

Taking limit,

$$\lim _{\Delta x_{i}\to 0}\sum _{i}\underbrace {\frac {\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}}{\Delta x_{i}}} _{\text{density}}\cdot \Delta x_{i}=\int _{S}\underbrace {f(x)} _{\text{density}}\,dx,$$

in which, intuitively and non-rigorously, $f(x)\,dx$ can be interpreted as the probability over 'infinitesimal' interval $[x,x+dx]$, i.e. $\mathbb {P} (X\in [x,dx])$, and $f(x)$ can be interpreted as the density of the probability over the 'infinitesimal' interval, i.e. ${\frac {\mathbb {P} (X\in [x,dx])}{dx}}$.

These motivate us to have the following definition.

Definition. (Continuous random variable) A random variable $X$ is continuous if

$$\mathbb {P} (X\in S)=\int _{S}f(x)\,dx$$

for each (measurable) set $S\subseteq \mathbb {R}$ and for some nonnegative function $f$.

Remark.

• The function $f$ is called probability density function (pdf), density function, or probability function (rarely).
• If $X$ is continuous, then the value of pdf at each single value is zero, i.e. $\mathbb {P} (X=x)=0$ for each real number $x$.

• This can be seen by setting $S=\{x\}$, then $\int _{S}f(u)\,du=\int _{x}^{x}f(u)\,du=0$ (dummy variable is changed).

• By setting $S=(-\infty ,x]$, the cdf $F(x)=\mathbb {P} {\big (}X\in (-\infty ,x]{\big )}=\int _{-\infty }^{x}f(u)\,du$.
• Measurability will not be emphasized. The sets encountered in this book are all measurable.
• $\int _{S}f(x)\,dx$ is the area of pdf under $S$, which represents probability (which is obtained by integrating the density function over the set $S$).

The name continuous r.v. comes from the result that the cdf of this kind of r.v. is continuous.

Proposition. (Continuity of cdf of continuous random variable) If a random variable $X$ is continuous, its cdf $F$ is also continuous (not just right-continuous).

Proof. Since $\lim _{h\to 0}F(x+h)=\lim _{h\to 0}\int _{-\infty }^{x+h}f(u)\,du=\int _{-\infty }^{x}f(x)\,dx=F(x)$ (Riemann integral is continuous), the cdf is continuous.

$\Box$

Example. (Exponential distribution) The function $F(x)=(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}$ is a cdf of a continuous random variable since

• It is nonnegative.
• $\int _{-\infty }^{\infty }(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}\,dx=\int _{0}^{\infty }(1-e^{-\lambda x})\,dx=1-(1-\underbrace {e^{0}} _{1})=1$. So, $\lim _{x\to \infty }F(x)=1$.
• It is nondecreasing.
• It is right-continuous (and also continuous).

Exercise.

1 Which of the following is (are) pdf?

	$f(x)=\mathbf {1} \{x\geq 0\}/x$
	$f(x)=\mathbf {1} \{x\geq 0\}/x^{2}$
	$f(x)=\mathbf {1} \{3\leq x\leq 8\}/5$
	$f(x)=\mathbf {1} \{0\leq x\leq 1\}x$
	$f(x)=\mathbf {1} \{0\leq x\leq {\sqrt {2}}\}({\sqrt {2}}-x)$

2 Compute $k$ such that the function $f(x)=k\mathbf {1} \{0\leq x\leq k/4\}x$ is a pdf.

	$1$
	$2^{1/3}$
	${\sqrt {2}}$
	$2$
	There does not exist such $k$.

3 Compute $k$ such that the function $F(x)=k\mathbf {1} \{0\leq x\leq k/4\}x$ is a cdf.

	$1$
	$2^{1/3}$
	${\sqrt {2}}$
	$2$
	There does not exist such $k$.

4 Which of the following is (are) true?

	If the support of a random variable is countable, then it is discrete.
	If the support of a random variable is not countable, then it is continuous.
	If the support of a random variable is not countable, then it is not discrete.

Proposition. (Finding pdf using cdf) If cdf $F(x)$ of a continuous random variable is differentiable, then the pdf $f(x)=F'(x)$.

Proof. This follows from fundamental theorem of calculus:

$$F'(x)={\frac {d}{dx}}\int _{-\infty }^{x}f(u)\,du=f(x).$$

$\Box$

Remark. Since $F(x)$ is nondecreasing, $F'(x)\geq 0\Rightarrow f(x)\geq 0$. This shows that $f(x)$ is always nonnegative if $F$ is differentiable. It is a motivation for us to define pdf to be nonnegative.

Without further assumption, pdf is not unique, i.e. a random variable may have multiple pdf's, since, e.g., we may set the value of pdf to be a real number at a single point outside its support (without affecting the probabilities, since the value of pdf at a single point is zero regardless of the value), and this makes another valid pdf for a random variable. To tackle this, we conventionally set $f(x)=0$ for each $x\notin \operatorname {supp} (X)$ to make the pdf become unique, and make the calculation more convenient.

Example. (Uniform distribution) Given that

$$f(x)=\mathbf {1} \{1\leq x\leq 5\}/4$$

is a pdf of a continuous random variable $X$, the probability $\mathbb {P} (2<X<3)=\int _{2}^{3}f(x)\,dx=\int _{2}^{3}(1/4)\underbrace {\mathbf {1} \{1\leq x\leq 5\}} _{=1\;{\text{under the integration region}}}\,dx=3/4-2/4=1/4.$

Exercise.

It is given that the function $f(x)=\mathbf {1} \{1\leq x\leq 6\}e^{x}/(e^{6}-e)$ is a pdf of a continuous random variable $X$.

1 Compute $\mathbb {P} (X>3)$.

	${\frac {e^{6}-e^{3}}{e^{6}-e}}$
	${\frac {e^{3}-e}{e^{6}-e}}$
	${\frac {e^{3}}{e^{6}-e}}$
	$e^{3}-e$
	$e^{6}-e^{3}$

2 Compute $\mathbb {P} (X>3|X<4)$.

	${\frac {e^{4}-e}{e^{4}-e^{3}}}$
	${\frac {e^{3}-e}{e^{4}-e^{3}}}$
	${\frac {e^{4}-e^{3}}{e^{4}-e}}$
	${\frac {e^{3}-e}{e^{4}-e}}$
	$1$

3 Compute $\mathbb {P} (X>3|X\geq 4)$.

	$1-{\frac {e^{4}-e}{e^{4}-e^{3}}}$
	$1-{\frac {e^{3}-e}{e^{4}-e^{3}}}$
	$1-{\frac {e^{4}-e^{3}}{e^{4}-e}}$
	$1-{\frac {e^{3}-e}{e^{4}-e}}$
	$0$

Mixed random variables

You may think that a random variable can either be discrete or continuous after reading the previous two sections. Actually, this is wrong. A random variable can be neither discrete nor continuous. An example of such random variable is mixed random variable, which is discussed in this section.

Theorem. (cdf decomposition) The cdf $F(x)$ of each random variable $X$ can be decomposed as a sum of three components:

$$F(x)=\alpha _{d}F_{d}(x)+\alpha _{c}F_{c}(x)+\alpha _{s}F_{s}(x)$$

for some nonnegative constants $\alpha _{d},\alpha _{c},\alpha _{s}$ such that $\alpha _{d}+\alpha _{c}+\alpha _{s}=1$, in which $x$ is a real number, $F_{d},F_{c},F_{s}$ is cdf of discrete, continuous, and singular random variable respectively.

Remark.

• If $\alpha _{d}\neq 0$ and $\alpha _{c}\neq 0$, then $X$ is a mixed random variable.
• We will not discuss singular random variable in this book, since it is quite advanced.
• One interpretation of this formula is:
  $$X={\begin{cases}{\text{discrete random variable having cdf }}F_{d}{\text{ with probability }}\alpha _{d};\\{\text{continuous random variable having cdf }}F_{c}{\text{ with probability }}\alpha _{c};\\{\text{singular random variable having cdf }}F_{s}{\text{ with probability }}\alpha _{s}.\end{cases}}$$
• If $X$ is discrete (continuous) random variable, then $\alpha _{c}=\alpha _{s}=0$ ($\alpha _{d}=\alpha _{s}=0$).
• We may also decompose pdf similarly, but we have different ways to find pdf of discrete and continuous random variable from the corresponding cdf.

An example of singular random variable is the Cantor distribution function (sometimes known as Devil's Staircase), which is illustrated by the following graph. The graph pattern keeps repeating when you enlarge the graph.

Cantor distribution function

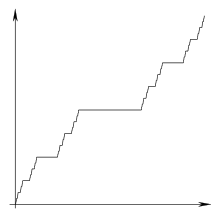
Example. Let $F_{d}(x)={\frac {1}{3}}\mathbf {1} \{x\geq 3\}+{\frac {2}{3}}\mathbf {1} \{x\geq 7\}$. Let $F_{c}(x)=\mathbf {1} \{x\geq 1\}(x-1)/(x+1)$. Then, $F(x)=(1/2)F_{d}(x)+(1/2)F_{c}(x)$ is a cdf of a mixed random variable $X$, with probability $1/2$ to be discrete and probability $1/2$ to be continuous, since it is nonnegative, nondecreasing, right-continuous and $\lim _{x\to \infty }F(x)=(1/2)\left[\lim _{x\to \infty }(F_{d}(x)+F_{c}(x)\right]=(1/2)(1+1)=1$.

Exercise. Consider the function $F(x)={\frac {\mathbf {1} \{x\geq 8\}+(1-1/x)\mathbf {1} \{x\geq 1\}}{k}}$. It is given that $F(x)$ is a cdf of a random variable $X$.

(a) Show that $k=2$.

(b) Show that the pdf of $X$ is

$$f(x)={\frac {1}{2}}(\mathbf {1} \{x=8\}+x^{-2}\mathbf {1} \{x\geq 1\}).$$

(c) Show that the probability for $X$ to be continuous is $1/k$.

(d) Show that $\mathbb {P} (X\geq 3|X\leq 8)$ is $2/3$.

(e) Show that the events $\{X\geq 3\}$ and $\{X\leq m\}$ are independent if $m\geq 8$ .

Proof.

(a) Since $F$ is a cdf, and $\mathbf {1} \{x\geq 8\}=\mathbf {1} \{x\geq 1\}=1$ when $x\to \infty$,

$$\lim _{x\to \infty }F(x)=1\implies {\frac {1+1}{k}}=1\implies k=2.$$

(b) Since $X$ is a mixed random variable, for the discrete random variable part, the pdf is

$$f_{d}(x)=\mathbf {1} \{x=8\}/2.$$

On the other hand, for the continuous random variable part, the pdf is

$$f_{c}(x)=\mathbf {1} \{x\geq 1\}x^{-2}/2.$$

Therefore, the pdf of $X$ is

$$f(x)={\frac {1}{2}}(\mathbf {1} \{x=8\}+x^{-2}\mathbf {1} \{x\geq 1\})$$

(c) We can see that $F(x)$ can be decomposed as follows:

$$F(x)={\frac {1}{2}}(\mathbf {1} \{x\geq 8\})+{\frac {1}{2}}((1-1/x)\mathbf {1} \{x\geq 1\}).$$

Thus, the probability for $X$ to be continuous is $1/k=1/2$.

(d)

$$\mathbb {P} (X\geq 3|X\leq 8)={\frac {\mathbb {P} (3\leq X\leq 8)}{\mathbb {P} (X\leq 8)}}={\frac {\mathbb {P} (X\leq 8)-\mathbb {P} (X\leq 3)+\overbrace {\mathbb {P} (X=3)} ^{0}}{1}}=1-\overbrace {(1-1/3)/2} ^{1/3}=2/3.$$

(e) If $m\geq 8$, $\mathbb {P} (X\leq m)=1$. Thus,

$$\mathbb {P} (X\geq 3\cap X\leq m)=\mathbb {P} (X\leq m)-\mathbb {P} (X\leq 3)+\underbrace {\mathbb {P} (X=3)} _{0}=1-\mathbb {P} (X\leq 3)=\mathbb {P} (X>3)=\mathbb {P} (X>3)+\underbrace {\mathbb {P} (X=3)} _{0}=\mathbb {P} (X\geq 3)=\mathbb {P} (X\geq 3)\underbrace {\mathbb {P} (X\leq m)} _{1},$$

i.e. $\{X\geq 3\}$ and $\{X\leq m\}$ are independent.

$\Box$