From Wikibooks, open books for an open world
1
Z
=
1
Z
R
+
1
Z
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}}
1
Z
=
1
R
+
j
ω
C
=
j
ω
C
R
+
1
R
{\displaystyle {\frac {1}{Z}}={\frac {1}{R}}+j\omega C={\frac {j\omega CR+1}{R}}}
Z
=
R
1
j
ω
C
R
+
1
{\displaystyle Z=R{\frac {1}{j\omega CR+1}}}
I
=
I
R
+
I
C
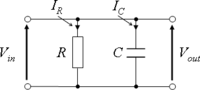
{\displaystyle I=I_{R}+I_{C}}
I
=
V
R
+
C
d
V
d
t
{\displaystyle I={\frac {V}{R}}+C{\frac {dV}{dt}}}
V
=
(
I
R
−
R
C
d
V
d
t
)
{\displaystyle V=(IR-RC{\frac {dV}{dt}})}
1
Z
=
1
Z
R
+
1
Z
L
{\displaystyle {\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}}
1
Z
=
1
R
+
1
j
ω
L
=
R
+
j
ω
L
j
ω
R
L
{\displaystyle {\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}={\frac {R+j\omega L}{j\omega RL}}}
Z
=
j
ω
R
L
R
+
j
ω
L
=
j
ω
L
1
1
+
j
ω
L
R
{\displaystyle Z={\frac {j\omega RL}{R+j\omega L}}=j\omega L{\frac {1}{1+j\omega {\frac {L}{R}}}}}
I
=
I
R
+
I
L
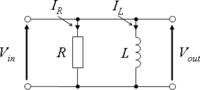
{\displaystyle I=I_{R}+I_{L}}
I
=
V
R
+
1
L
∫
V
d
t
{\displaystyle I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt}
V
=
I
R
−
R
L
∫
V
d
t
{\displaystyle V=IR-{\frac {R}{L}}\int Vdt}
1
Z
=
1
Z
L
+
1
Z
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}}
1
Z
=
1
j
ω
L
+
j
ω
C
=
(
j
ω
)
2
L
C
+
1
j
ω
L
{\displaystyle {\frac {1}{Z}}={\frac {1}{j\omega L}}+j\omega C={\frac {(j\omega )^{2}LC+1}{j\omega L}}}
Z
=
j
ω
L
(
j
ω
)
2
L
C
+
1
{\displaystyle Z={\frac {j\omega L}{(j\omega )^{2}LC+1}}}
I
=
I
L
+
I
C
{\displaystyle I=I_{L}+I_{C}}
I
=
1
L
∫
V
d
t
+
C
d
V
d
t
{\displaystyle I={\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}}
1
Z
=
1
Z
R
+
1
Z
L
+
1
Z
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}}
1
Z
=
1
R
+
1
j
ω
L
+
j
ω
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C}
1
Z
=
(
j
ω
)
2
R
L
C
+
j
ω
L
+
R
j
ω
R
L
{\displaystyle {\frac {1}{Z}}={\frac {(j\omega )^{2}RLC+j\omega L+R}{j\omega RL}}}
1
Z
=
(
j
ω
)
2
L
C
+
j
ω
L
R
+
1
j
ω
L
{\displaystyle {\frac {1}{Z}}={\frac {(j\omega )^{2}LC+j\omega {\frac {L}{R}}+1}{j\omega L}}}
I
=
I
R
+
I
L
+
I
C
{\displaystyle I=I_{R}+I_{L}+I_{C}}
I
=
V
R
+
1
L
∫
V
d
t
+
C
d
V
d
t
{\displaystyle I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}}
I
=
V
R
+
1
L
∫
V
d
t
+
C
d
V
d
t
{\displaystyle I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}}
V
=
I
R
−
R
L
∫
V
d
t
−
C
R
d
V
d
t
{\displaystyle V=IR-{\frac {R}{L}}\int Vdt-CR{\frac {dV}{dt}}}
0
=
V
R
+
1
L
∫
V
d
t
+
C
d
V
d
t
{\displaystyle 0={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}}
I
t
=
I
R
+
L
d
I
d
t
+
1
C
∫
I
d
t
{\displaystyle I_{t}=IR+L{\frac {dI}{dt}}+{\frac {1}{C}}\int Idt}
Second ordered equation that has two roots
ω = -α ±
α
2
−
β
2
{\displaystyle {\sqrt {\alpha ^{2}-\beta ^{2}}}}
Where
α
=
R
2
L
{\displaystyle \alpha ={\frac {R}{2L}}}
β
=
1
L
C
{\displaystyle \beta ={\frac {1}{\sqrt {LC}}}}
The current of the network is given by
A eω1 t + B eω2 t From above
When
α
2
=
β
2
{\displaystyle {\alpha ^{2}=\beta ^{2}}}
ω = -α When
α
2
>
β
2
{\displaystyle {\alpha ^{2}>\beta ^{2}}}
ω = -α ±
α
2
−
β
2
{\displaystyle {\sqrt {\alpha ^{2}-\beta ^{2}}}}
When
α
2
<
β
2
{\displaystyle {\alpha ^{2}<\beta ^{2}}}
ω = -α ± j
β
2
−
α
2
{\displaystyle {\sqrt {\beta ^{2}-\alpha ^{2}}}}
At resonance, the impedance of the frequency dependent components cancel out . Therefore the net voltage of the circui is zero
Z
L
−
Z
C
=
0
{\displaystyle Z_{L}-Z_{C}=0}
V
L
+
V
C
=
0
{\displaystyle V_{L}+V_{C}=0}
ω
L
=
1
ω
C
{\displaystyle \omega L={\frac {1}{\omega C}}}
ω
=
1
L
C
{\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}
Z
=
Z
R
+
(
Z
L
−
Z
C
)
=
Z
R
=
R
{\displaystyle Z=Z_{R}+(Z_{L}-Z_{C})=Z_{R}=R}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
At Resonance Frequency
ω
=
1
L
C
{\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
Further analyse the circuit
At ω = 0, Capacitor Opened circuit . Therefore, I = 0 .
At ω = 00, Inductor Opened circuit . Therefore, I = 0 .
1
L
C
{\displaystyle {\sqrt {\frac {1}{LC}}}}
I
=
V
2
R
{\displaystyle I={\frac {V}{2R}}}
1 - ω2 where ω1 = ωo - Δω, ω2 = ωo + Δω
In RLC series, it is possible to have a band of frequencies where current is stable, ie. current does not change with frequency . For a wide band of frequencies respond, current must be reduced from it's peak value . The more current is reduced, the wider the bandwidth . Therefore, this network can be used as Tuned Selected Band Pass Filter . If tune either L or C to the resonance frequency
ω
=
1
L
C
{\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
If R is increased from R to 2R then the current now is
I
=
V
2
R
{\displaystyle I={\frac {V}{2R}}}
ω1 - ω2 where
ω1 = ωo - Δω
ω2 = ωo + Δω For value of I <
I
=
V
2
R
{\displaystyle I={\frac {V}{2R}}}
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
I
=
V
2
R
{\displaystyle I={\frac {V}{2R}}}
Circuit
Symbol
Series
Parallel
RC
A parallel RC Circuit
Impedance
Z
Z
t
=
R
+
1
ω
C
=
ω
C
R
+
1
ω
C
{\displaystyle Z_{t}=R+{\frac {1}{\omega C}}={\frac {\omega CR+1}{\omega C}}}
1
Z
t
=
1
Z
R
+
1
Z
C
=
1
R
+
ω
C
=
R
ω
C
R
+
1
{\displaystyle {\frac {1}{Z_{t}}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}={\frac {1}{R}}+\omega C={\frac {R}{\omega CR+1}}}
Frequency
ω
o
=
2
f
o
{\displaystyle \omega _{o}=2f_{o}}
Z
R
=
Z
C
{\displaystyle Z_{R}=Z_{C}}
R
=
1
ω
C
{\displaystyle R={\frac {1}{\omega C}}}
ω
=
1
C
R
{\displaystyle \omega ={\frac {1}{CR}}}
1
R
=
1
ω
C
{\displaystyle {\frac {1}{R}}={\frac {1}{\omega C}}}
1
R
=
ω
C
{\displaystyle {\frac {1}{R}}=\omega C}
ω
=
1
C
R
{\displaystyle \omega ={\frac {1}{CR}}}
Voltage
V
V
=
I
R
+
1
C
∫
I
d
t
{\displaystyle V=IR+{\frac {1}{C}}\int Idt}
I
=
V
R
+
C
d
V
d
t
{\displaystyle I={\frac {V}{R}}+C{\frac {dV}{dt}}}
Current
I
∫
I
d
t
=
C
(
V
−
I
R
)
{\displaystyle \int Idt=C(V-IR)}
d
V
d
t
=
1
C
(
I
−
V
R
)
{\displaystyle {\frac {dV}{dt}}={\frac {1}{C}}(I-{\frac {V}{R}})}
Phase Angle
Tan θ = 1/2πf RC
Tan θ = 1/2πf RC