High School Chemistry/Shapes of Atomic Orbitals
In the last lesson, we learned how the principal quantum number determines the size of an electron wave (and the number of nodes), ℓ determines the shape of an electron wave, and m1 determines the orientation of an electron wave. Now the effects of n are probably easy to visualize. For bigger values of n, the electron wave gets bigger, and it ends up with more nodes. Similarly, the effects of ml are easy to visualize as well. For different values of ml, the electron wave gets rotated into different orientations. In other words, the electron wave points in different directions. What about the effects of ℓ? You know that ℓ tells you something about the shape of the electron wave. You also know that certain waves are spherical while others are dumb-bell shaped, or butterfly shaped or just plain crazy shaped! But how do you know which value of ℓ corresponds to which shape?
Unless you have a lot of training in mathematics, and can understand the wave function, there's really no way for you to predict what the shape of a wave with a particular value of ℓ will look like. Really, you just have to know, or be told – so that's what we'll do in the next few sections. We'll tell you what an ℓ = 0 wave looks like, and what an ℓ = 1 wave looks like.
Lesson Objectives[edit | edit source]
- Define an electron orbital.
- Be able to recognize s orbitals by their shape.
- Be able to recognize p orbitals by their shape.
When the Azimuthal Quantum Number is 0, The Electron Occupies an s Orbital[edit | edit source]
In the last lesson, you learned that different electron wave shapes have different names and that these names are always letters of the alphabet like s, p, d, and f. (These letters were chosen on the basis of observations of line spectra. Certain lines were observed as a "sharp" series; others were classified as "principal", "diffuse", or "fundamental" series, thus s, p, d, f.) These letters correspond to the shape of the electron wave, or at least the shape that the electron wave appears to take as a result of its electron density being thicker in one place than it is in the other. Now, this can get a little confusing, but remember, electron waves describe electron density or electron "fog" which comes from interpreting the wave-like properties of the electron. Nevertheless, we always have to be careful that we don’t forget about the particle-like properties of the electron as well. As a result, once scientists know the shape of a particular electron wave, they will often switch and start describing the electron as a particle again. To do this, they use the name for the shape of the wave, but rather than saying "the electron wave has an s shape", or "the electron wave has a p shape", they will say "the electron is in an s orbital", or "the electron is in a p orbital". This makes it sound as if the electron is a particle again, and as if the orbital is some sort of box that the particle is confined to, or at least some sort of territory that the particle patrols.
This switching back and forth between the wave-like description of the electron and the particle-like description of the electron may seem confusing, or annoying, or just plain strange, but scientists do it to remind themselves that electrons are both particles and waves. So exactly what is an orbital? Technically speaking, an orbital is a wave function for an electron defined by the three quantum numbers, n, ℓ, and ml. What the wave function describes, though, is a region in space with a particular shape, where you are likely to find an electron. In terms of waves, the orbital describes the region in space where the electron density is very thick. In terms of particles, the orbital describes the region in space where there is a high probability of finding the electron (which should make sense, because wherever the electron density is thick, there is also a high probability of finding the electron).
So far we've decided that ℓ describes the shape of an orbital, which in turn describes where the electron density is thick (and there is a high probability of finding the electron) and where the electron density is thin (and there is a low probability of finding the electron). We're still, however, working towards a description of what these waves with regions of thick and thin electron density actually look like. Let's begin with the simplest wave shape. The simplest wave shape occurs for ℓ = 0. Whenever an electron wave is described by the quantum number ℓ = 0, we say that the wave function describes what's known as an s wave and thus the electron is in an s orbital. s waves can be big or small, depending on the value of n. s waves can also have a huge number of nodes or no nodes at all, again depending on the value of n. What all s waves have in common, though, is their shape. That's what we'll talk about in the next section.
s Sublevels are Spherically Shaped[edit | edit source]
All ℓ = 0 electron waves are s waves, or waves from the s sublevel, and they all describe electrons in s orbitals. As suggested in the previous section, all electron waves from the s sublevel have the same overall shape, regardless of the value of n, regardless of their size, and regardless of the number of nodes they contain. s orbitals always correspond to spherical waves. The quantum numbers n = 1 and ℓ = 0 describe a small spherical wave with no nodes, the quantum numbers n = 2 and ℓ = 0 describe a larger spherical wave with a single node, and the quantum numbers n = 3 and ℓ = 0 describe an even larger spherical wave with two nodes. These waves all look slightly different, as shown in Figure 6.16.


Nevertheless, they are all spherical, because they all have ℓ = 0. Their shapes don't change – only their sizes and the number of nodes that they contain.
Now if you think back to an earlier lesson, you might remember something special about the different orientations of a spherical wave. Do you remember what happened when we rotated the spherical wave so that it pointed in different directions? It ended up looking the same, didn't it! No matter which way you rotate a sphere, it always looks the same. So how many different ml values do you expect for a spherical wave? One, of course! Now that you know spherical waves all have ℓ = 0, you can use your rules for ml to figure out exactly how many different ml are allowed. If you look back to Example 4 in the previous lesson, you'll see that we actually did that calculation. It turned out that there was only one allowable value for ml, and that was ml = 0. In other words, there is only one orientation of a spherical wave. It all makes sense!
So what does a spherical wave really mean? It means that your probability of finding an electron at any particular distance from the center of the atom only depends on the distance, and not on the direction. You can see this in Figure 6.17.
When the Azimuthal Quantum Number is 1, then ml Can Only Be -1, 0, or +1[edit | edit source]
All ℓ = 1 electron waves are p waves, or waves from the p sublevel, and they describe electrons in what are known as p orbitals. Unlike s orbitals, p orbitals are not spherical, so they can have different orientations in space. Now that you know all p orbitals have ℓ = 1, you should be able to figure out exactly how many different p orbital orientations exist by using your rules for ml. (ml is the quantum number associated with the orientation of a particular orbital). Let's figure it out.
|
Example 1 How many different p orbital orientations are possible? Solution: ℓ = 1 From now on, whenever you're told an electron is in a p orbital, you're expected to know that electron has the quantum number ℓ = 1. The question asks how many p orbital orientations are possible, but what it's really asking is how many different ml values are allowed when ℓ = 1. We've already done this type of problem. 1. Find the minimum value of ml.
2. Find the maximum value of ml.
3. List all of the integers (no decimals!) starting from the minimum value of ml and ending with the maximum value of ml.
In this case ml can equal −1, 0 or 1, so there are a total of 3 allowed values for ml, and thus 3 possible p orbital orientations. |
The p Orbitals are Often Described as Dumb-bell Shaped[edit | edit source]
Even though you know that there are three possible orientations for p orbitals, you can't really predict their shape unless you know a lot more about mathematics, physics, and wave functions. When scientists use the wave function to draw the shape of an electron's p orbital, though, they always end up with is something that looks a lot like a dumb-bell. Not only that, the three different p orbitals (one with ml = −1, another with ml = 0, and the third with ml = 1) turn out to be perpendicular to each other. In other words, if one p orbital points along the x-axis, another p orbital points along the y-axis, and the third points along the z-axis. Scientists typically label these three orbitals px, py, and pz respectively. The below figure shows each of the three p orbitals separately, and then all three together on the same atom.

Sometimes we get so caught up thinking about electron wave functions, and electron orbitals, that we forget entirely about the atom itself. Remember, electron standing waves form because electrons get trapped inside an atom by the positive charge on the atom's nucleus. As a result, s orbitals, and p orbitals and even d and f orbitals always extend out from the atom's nucleus. Don't get so caught up in orbitals that you forget where they are and why they exist.
As with s orbitals, p orbitals can be big or small, depending on the value of n, and they can also have more or less nodes, also depending on the value of n. Notice, however, that unlike the s orbital, which can have no nodes at all, a p orbital always has at least one node. Take a look at the p orbital figure above again. Can you spot the node in each of the p orbitals? Since all p orbitals have at least one node, there are no p orbitals with n = 1. In fact, the first principal quantum number, n, for which p orbitals are allowed is n = 2. Of course you could have figured that out for yourself, right? No? Well, here’s a hint – remember the rules for predicting which values of ℓ are allowed for any given value of n. In the last lesson, you learned that ℓ must be no less than 0, but also, no greater than n − 1. For the n = 1 energy level, then, the maximum allowed value for ℓ is:
- maximum ℓ = n − 1
- maximum ℓ = 1 − 1
- maximum ℓ = 0
As a result, only s orbitals (ℓ = 0) are allowed. For the n = 2 energy level, though, the maximum allowed value for ℓ is
- maximum ℓ = n − 1
- maximum ℓ = 2 − 1
- maximum ℓ = 1
which means p orbitals (ℓ = 1) are allowed as well. So now you see that the restrictions on ℓ are actually there to make sure that all n = 1 wave functions have no nodes, all n = 2 wave functions have 1 node, all n = 3 wave functions have 2 nodes, all… well, you get the picture.
One interesting property of p orbitals that is different from s orbitals is that the total amount of electron density changes with both the distance from the center of the atom and the direction. Take a look at Figure 6.18. Notice how the electron density is different depending on which direction you travel from the center of the atom out. In the particular p orbital shown, the probability of finding the electron is greater as you head straight up from the center of the atom than it is as you head straight to the left or to the right of the atom. It turns out that this dependence on direction is very important when it comes to studying how different atoms interact and form bonds. We'll talk more about that in a later chapter.

The d Orbitals and f Orbitals are Not Easily Visualized[edit | edit source]
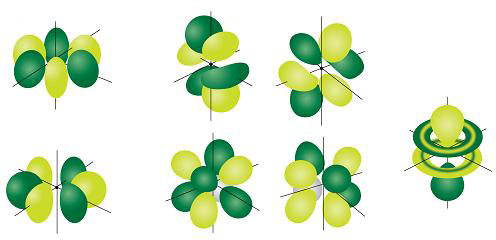
Did you notice how the p orbitals looked a lot fancier than the simple spherical s orbitals? Well, you can imagine that if p orbitals with ℓ = 1 are fancy, then d orbitals, with ℓ = 2 are even fancier, and f orbitals, with ℓ = 3 are just plain crazy! Most people can visualize p orbitals, but d orbitals and f orbitals are actually rather difficult to imagine. Most d orbitals are butterfly shaped, although one has an unusual shape that looks like a doughnut surrounding a Q-tip! The 5 possible d orbitals are shown in Figure 6.19 (and you could have figured out that there were 5, right?). Don't worry too much about why one of the d orbitals is different. Again, it takes a lot of complex math to understand where the different d orbital pictures came from, and you won't have to worry about that unless you decide to go on and study quantum chemistry at the university level. As for f orbitals, they are even hard to draw, not to mention the fact that there are a total of 7 of them (Figure 6.20)! We won't be too concerned with d orbitals in this course, although they do become very important if you want to study certain metals like those found in the center of the periodic table. Similarly, f orbitals aren't all that important when it comes to common chemicals like hydrogen, or oxygen, or even copper. They do become important, though when you want to study some of the most important radioactive elements like uranium and plutonium!

Lesson Summary[edit | edit source]
- An orbital is a wave function for an electron defined by the three quantum numbers, n, ℓ and ml. Orbitals define regions in space where you are likely to find electrons.
- s orbitals (ℓ = 0) are spherical shaped.
- p orbitals (ℓ = 1) are dumb-bell shaped.
- The three possible p orbitals are always perpendicular to each other.
Review Questions[edit | edit source]
Fill in the blanks.
- When ℓ = 0, the electron orbital is _________ and when ℓ = 1, the electron orbital is _________ shaped.
- The n = 1 s orbital has _____ nodes.
- The n = 2 s orbital has _____ nodes.
- The n = 2 p orbital has _____ nodes.
- The n = 1 p orbital has _____ nodes.
- There are ____ different p orbitals.
- What energy level (or value of n) has s, p and d orbitals, but no f orbitals?
- How many different d orbital orientations are there?
- How many f orbital orientations are there?
- How many different orbitals are there in the n = 3 energy level?
Vocabulary[edit | edit source]
- orbital
- A wave function for an electron defined by all three quantum numbers, n, ℓ, and ml. Orbitals define regions in space where there is a high probability of finding the electron.
This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License