Geometry for Elementary School/Copying a line segment
Jump to navigation
Jump to search
This construction copies a line segment to a target point T. The construction is based on Book I, prop 2.
The construction[edit | edit source]
- Let A be one of the end points of . Note that we are just giving it a name here. (We could replace A with the other end point B).

- Draw a line segment

- Construct an equilateral triangle (a triangle that has as one of its sides).
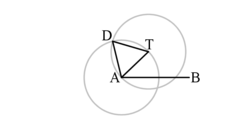
- Draw the circle , whose center is A and radius is .

- Draw a line segment starting from D going through A until it intersects and let the intersection point be E . Get segments and .

- Draw the circle , whose center is D and radius is .

- Draw a line segment starting from D going through T until it intersects and let the intersection point be F. Get segments and .

Claim[edit | edit source]
The segment is equal to and starts at T.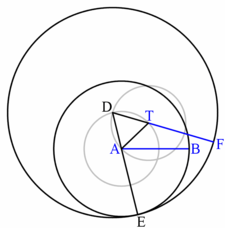
Proof[edit | edit source]
- Segments and are both from the center of to its circumference. Therefore they equal to the circle radius and to each other.
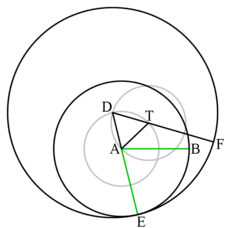
- Segments and are both from the center of to its circumference. Therefore they equal to the circle radius and to each other.

- equals to the sum of its parts and .
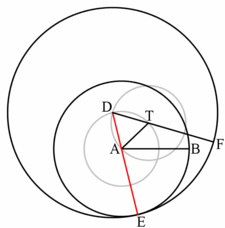
- equals to the sum of its parts and .

- The segment is equal to since they are the sides of the equilateral triangle .
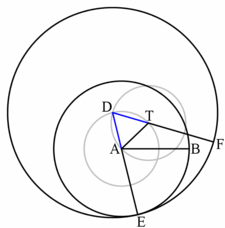
- Since the sum of segments is equal and two of the summands are equal so are the two other summands and .
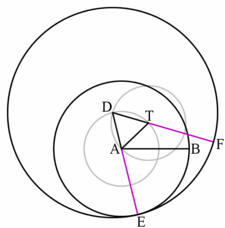
- Therefore equals .

























