General Astronomy/Motion and Gravity
| General Astronomy | ||
| Observational Astronomy | Motion and Gravity | Principles of Light |
The Early Origins of Astronomy

Thousands of years ago, the night sky was much more a part of everyday life than it is today. Without light pollution from streetlights, anyone could see thousands of stars or the path of the Milky Way through the sky. The motion of the stars provided an essential calendar for predicting the weather, so ancient people were accordingly very attentive and observant of the heavens and the rest of their surroundings. These ancient observations were the foundation for what would become modern astronomy, and were the first manifestations of scientific thought in society.
A central principle in scientific reasoning is that the world is inherently orderly and capable of being understood, and that observation is the means by which we can learn about how the universe works. There is, however, nothing that requires the universe to make sense or be accessible to human understanding. Humanity has placed trust in the ideas behind the scientific method because science has been so successful, and so much of the world really does obey a set of rules.
The ingredients that make up a successful philosophy of science were not conceived all at once, but rather in a gradual process of development over the entire course of history. The ancients could never have known in advance which principles of scientific method would eventually prove to be reliable. In its adolescence, society stumbled through the dark to learn about the world, to discover how their experiences could teach them what the universe was like, and to identify the boundaries between reason and superstition. The story of the development of science in cultures throughout the world is revealing not only of the nature of the world and of truth, but also of human nature more generally.
Ancient artifacts going as far back as 20 thousand years, to the paleolithic age, may arguably be related to astronomy, although the interpretation of such artifacts is a subject of controversy. The best-known examples are found in the caves of Lascaux in France, where a variety of paleolithic artwork are found. Some specimens found in the caves might possibly depict the Pleiades star cluster or the zodiac. Animal bones nearby have markings such that they could have been used as a lunar calendar. Although artifacts from the paleolithic era are scarce and ambiguous, this scarcity does not necessarily imply that the peoples of the period took no interest in the heavens. Modern aboriginal cultures, for example, pass down ceremonies with strong astronomical symbolism that would not reflect themselves in archaeological artifacts.

The character of artifacts of the neolithic period is markedly different, since understanding of the skies and the calendar clearly bear deep meaning for agricultural cultures in even the earliest times. Observers gained the ability to manage the planning of significant annual events. The motions of the heavens develop a profound influence on the affairs of humanity, and this influence comes to manifest itself in religious interpretations of heavenly phenomena and worship of the planets, practices that form the origins of both astrology and astronomy.
Ancient monuments and markers demonstrate societies' early interest in the heavens to archaeologists and historians. Many graves of this period are aligned with the cardinal directions. Ancient monuments and altars of sacrifice face east, south, or west to within a few degrees — a clear indication that neolithic peoples had begun very early to identify the most fundamental concepts of astronomy. The most famous of the ancient monuments is Stonehenge. The stones of the monument mark the positions of sunrise on the summer solstice, among other things.
Several of the planets have been known since prehistoric times. These bodies are very bright, and they wander among the fixed stars, through the constellations. These were known to the Greeks as planētēs, "wanderers". The ancients knew of 7 "planets": the Sun, the Moon, Mercury, Venus, Mars, Jupiter, and Saturn. The names for the seven days of the week come from the Norse gods: Sunday (the Sun), Monday (the Moon), Tuesday (Mars/Tiw), Wednesday (Mercury/Wodan), Thursday (Jupiter/Thor), Friday (Venus/Frigg), and Saturday (Saturn/Soeternes).

Highly systematic and carefully recorded observation of the heavens appears as early as the third millennium BC, in the ancient Mesopotamian civilization of Babylon. The Babylonians also developed the earliest timekeeping instruments. Of perhaps even greater significance, however, was the birth of astrology in Mesopotamia. The astrologers of Babylon were the first to suppose a cause and effect relationship between heavenly and earthly events, and the first to imagine an underlying order in nature — though no real connection between human and celestial events existed, the prophecies of astrology were the ancestors of modern scientific prediction.
The early astronomers understood a great deal about the world around them. By Aristotle's time, many people believed that the world was round. They knew this from several sources of evidence:
- When ships sailed beyond the horizon, those watching from land would see the hull disappear first, and then would watch the sail disappear. Sailors see the land sink below the horizon bottom-first. From this, they gathered that the surface of the world was curved, and that the ship was moving around the curvature of the Earth.
- Ancient people supposed eclipses of the Moon to be the shadow of the Earth. Shadows seen during lunar eclipses were always round. The only shape that always casts a round shadow is a sphere. This suggested that the Earth was spherical.
- Travelers noticed that new stars became visible as they moved in their journeys. When travelers move north, the North Star and the northern constellations gain altitude in the sky. The ancients recognized that this implied that the Earth is curved.
Aristotle mentions in his writings that some thinkers of his time hold that the Earth is flat, while others believe it to be spherical. He himself argues firmly that the Earth is a sphere. After Aristotle's time, nearly all Western writers claim that the Earth is a sphere.

In the third century BC, the Hellenistic Egyptian scholar Eratosthenes served as head of the library of Alexandria, where he studied and wrote on a variety of subjects. During his studies, Eratosthenes learned that the Sun cast no shadow on midday of the summer solstice from the city of Syene. From Alexandria, Eratosthenes observed that the Sun did cast a shadow, and he measured that the angle between the Sun and the zenith was about seven degrees when the Sun was highest in the sky.
Eratosthenes knew he could measure the circumference of the Earth by measuring the distance between Alexandria and Syene, assuming that the Sun was at the highest point in both cities at the same time. Since 7 degrees is 7/360 of a circle, the distance between Syene and Alexandria must be 7/360 (or, equivalently, about 1/50) of the circumference of Earth.
Eratosthenes estimated the distance between Syene and Alexandria to be about 5,000 stadia, and concluded that the circumference of the Earth was about 50 times that, or 250,000 stadia. The stadium was a common unit of distance in the ancient world, comparable to kilometers or miles in modern usage; the exact length meant by a stadium varied over history and from region to region, so it is difficult to compare Eratosthenes's estimate with modern values. Most values of the stadium, however, translate to a circumference in the area of 40,000 kilometers, which is remarkably close to the accepted circumference of 40,070 kilometers.
As science was beginning to grow in the cultures of Western civilization, it was likewise taking root elsewhere in the world. Ancient and medieval China, India, and America in particular have been centers of the scientific world.
The history of science in India is one of the longest and best documented in the world. Largely isolated from the rest of the world through much of its earliest history, India was free to develop its unique flavor of astronomical practice at its own pace and without external influence. Ancient India had no system of astrology, but celestial timekeeping became popular very early. The first astronomers monitored the progression of the year and tracked the movement of the Sun, Moon, and planets through the nakshatra, the Indian zodiac.
The quality of these observations would make it possible for later Indian astronomers to detect the effects of precession, just as Hipparcos had done for Greek astronomy. Indian astronomers of the Middle Ages estimated the speed of precession to be 54 seconds per year. Although this is much more accurate than Hipparcos's measurement, we must note that the number 54 was chosen for mystical rather than scientific reasons. Ancient people throughout the world mixed mysticism with arithmetic in this way, but we see this much more consistently in the Indian culture than in any other.
The Christian era brought great change to Indian astronomy. By about the year AD 519, Babylonian conquest had spread into the Indus basin, and many Greek scholars had already visited or settled. Naturally, cultural exchange took root.
The ancient Chinese valued astronomy very highly. Systematic observation of the heavens may have begun in China as early as the third millennium BC. Science was viewed as a powerful tool and therefore guarded very closely by the state. Under dynastic rule, the perceived purpose of astrology and astronomy was to remind the people of the connection between the emperor and celestial events. Accordingly, astrology was charged specifically to an Astronomical Bureau appointed by the emperor and carried out according to strict rules.
The Chinese regarded celestial events as important omens, particularly in the case of "guest stars," stars that temporarily appeared in the sky and quickly faded away. Today we know that these are stellar explosions called supernovae. In the year AD 1054, a new supernova became bright enough to be visible even during the day. Chinese and Arab astronomers recorded the event, and it appears to be depicted in an American cave painting. Because of the importance the Chinese assigned to supernovae, their observations of ancient supernovae are by far the most complete in the world, and remain useful as a source of scientific data even today.

Meanwhile, astronomy was thriving in pre-Columbian America, where interest in the heavens was widespread. Astronomy held a high position in the Mayan civilization, which dominated Mesoamerica for two thousand years prior to the arrival of Europeans. The Maya people believed that patterns in nature were very important, and that it should be possible to use astrology to predict the future based on past experience. This made the observation of celestial cycles very important, since they would give advance knowledge of future events, and Mayans dutifully kept track of motions of the Sun and Moon. With the accumulation of centuries of observation, Mayan astronomers were able to predict eclipses and measure the lengths of heavenly cycles very well.
Similar ideas were sprouting throughout the Americas. Throughout the Americas, ancient people built monuments, buildings, mounds, and temples aligned with rising and setting points of important stars, or with the northernmost and southernmost positions of the Moon. Calendars and monuments like Stonehenge are found here. Clearly, interest in the heavens was common throughout the ancient world, as were the rudimentary beginnings of science.

Scientific thought has appeared throughout history and all over the world, but it's clear that the scientific enterprise enjoyed more success in some areas and time periods than in others. The reasons for this are entirely unclear. What factors of culture, economics, and philosophy affect the rise of scientific thought? The Babylonian culture, for example, did not permit deviation of any kind from tradition or conventional practice. Such a culture might be expected to hinder the progress of science, yet science and mathematics flourished there. In ancient China, only nobles were permitted to practice science. Some historians have suggested that this culture prevented a renaissance that might otherwise have occurred in China long before the European Renaissance. This question of the interplay between science and sociology has been the subject of great interest in the study of the history of science.
While magic and superstition were a significant part of early thought and difficult to isolate from the emerging pursuit of science, it would be unfair to say that spiritualism completely permeated the first ideas about the nature of the universe. The scientific spirit, the principle of learning about the universe by observing it, was clearly present even from the earliest times, and scientific thought has been remarkably widespread. Anaximander (611-547 BC) postulated that there were five elements: earth, air, fire, water...and quintessence, which heavenly bodies were made of.
Astrology is based on Ptolemy's Tetrabiblos, written in 140 AD. The horoscope is divided up into 12 "houses", 12 constellations along the ecliptic. Ptolemy believed that an "8th Sphere" held up the stars in the sky.
Kinetic energy is the energy of motion. The formula for this is ( is mass, and is velocity). Before the common acceptance of the heliocentric model in the mid 1500s, the Earth was believed to be the center of the known universe. Many inherent problems in the geocentric model of the universe led Nicolaus Copernicus to formulate an alternate means by which planets and stars moved. Two such problems are the apparent retrograde motion of various planets, specifically Mars, and the ensuing epicycle theory made to compensate for this issue, as well as the phases of Venus that occur.
Planetary Motion and Epicycles

Viewing Earth as the center of our universe, many of the planets in our solar system take on a peculiar motion across the night sky. For instance, Mars appears to move in a retrograde fashion from time to time. Since the geocentric model holds that all the planets in our solar system orbit the Earth, this would mean that from time to time Mars reverses its orbital direction only to resume it later. The Greek astronomer, Ptolemy, sought to explain this phenomenon with the use of epicycles - that is, small circular motions that planets orbiting the Earth followed on top of their circular orbit around the Earth. Astronomers from Greek times to the Enlightenment compensated for flaws in the geocentric model by adding extra layers of epicycles, until the system was so complex it became virtually unusable. Copernicus' heliocentric model, placing the Sun at the center with planets going around it rather than around the Earth, rid the universe of many of the epicycles that plagued astronomy at that time.
Phases of Venus
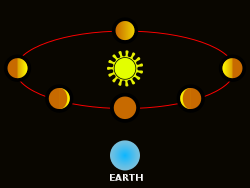

Another problem with the geocentric model occurred when observing Venus and its relative phases: should Venus and the Sun orbit the Earth, then it would be impossible for Venus to be in the "full" phase, that is complete illumination (similar to a full moon). Thus, the Ptolemaic model predicted only crescent and new phases of Venus. Yet, as Galileo observed, this was clearly not the case; Venus exhibited all phases of the moon, a phenomenon predicted and accounted for by Copernicus' model. Discovered by Galileo, this phenomenon was one of the key factors that would end up supporting the Heliocentric view of the universe.
Note that this is only one of a number of observations made by Galileo that contradicted the ancient beliefs, but this one most directly called into question the idea that planets orbit the Earth.
References
- Shea, William R. Galileo in Rome: the Rise and Fall of a Troublesome Genius. New York: Oxford UP, USA, 2004.
The modern heliocentric model of the universe was proposed by Nicolaus Copernicus in his book De revolutionibus orbium coelestium which was published just before his death to avoid prosecution for heresy. It addressed many of the problems associated with the Ptolemaic model which required a multitude of epicycles to describe planetary motion. Heliocentrism places the Sun at the center of the solar system. While some of the ancient civilizations in India and the Middle East had proposed the heliocentric model before, Copernicus' discovery set the groundwork for the modern view of the solar system.
Copernicus' Model

In Copernicus' heliocentric model, there are seven theories he presents:
- There exists more than one center of the universe.
- There is a center of the universe near the sun.
- The planet Earth is not the center of our universe.
- The scale of distances between the Earth and the Sun is minuscule compared with the astronomical distances between Earth and the stars in the sky.
- The Earth revolves around the sun, thus causing the annual cycles of the seasons that we witness.
- The Earth's own rotation causes the stars to appear to shift every night, rather than any motion of the stars themselves.
- Any retrograde motion, previously explained by epicycles, is in fact caused by the differing orbital velocities of planets around the sun.
Copernicus harbored his belief of heliocentrism for many years, and did not publish his work until 1542, a year before he died. Some speculate that Copernicus held onto his idea for a considerable time simply because he was fearful of the reception it would have among his peers and more importantly, the Church. Many consider the publication of De revolutionibus orbium coelestium (On the Revolution of the Celestial Sphere) to be the start of the Scientific Revolution.
In the years that followed, Copernicus' theory was refined and independently verified by notable scientists, most prominently Galileo and Kepler. Specifically, Galileo noted that all phases of Venus occurred (similar to our moon), which cannot be adequately explained in a geocentric model. This contradicted the solely new and crescent phases predicted by the geocentric model.
Acceptance by the Church
The principle behind rockets was discovered in 100 BC. An early rocket was the aeolipile, a steam-powered device. Johannes Kepler was a mathematician who attempted to derive a set of fundamental principles which would explain the motions of the planets. He believed in the heliocentric view of the solar system proposed by Copernicus, and he also possessed a rich set of observations of the planets made by Tycho Brahe.
After twenty years of painstaking attempts and various discarded ideas based on geometry, he finally arrived at a mathematical model of orbital motions based on the ellipse. Kepler summarized his findings in the form of three laws of planetary motion, frequently referred to as Kepler's First, Second and Third Laws, respectively:
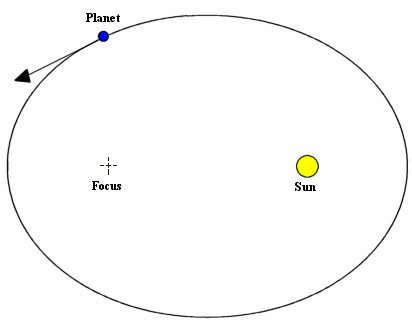
- Kepler's First Law, also known as The Law of Ellipses — The orbits of the planets are ellipses, with the sun at one focus.
- Kepler's Second Law, or The Law of Equal Areas in Equal Time — The line between a planet and the sun sweeps out equal areas in the plane of the planet's orbit over equal times.
- Kepler's Third Law, or The Law of Harmony — The time required for a planet to orbit the sun, called its period, is proportional to half the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets. It is often called the Law of Harmony because it shows a harmonic relation between distances and periods.
At that time he developed these laws, there was not yet a developed theory of gravity capable of explaining why the planets moved as they were observed to. Later, Isaac Newton, using his universal inverse-square law theory of gravity, was able to show how Kepler's Laws fit into a scientific theory of celestial mechanics.
Elliptical orbits
An ellipse is a shape formed by taking a diagonal slice through a cone. It is essentially the shape of a circle viewed at an angle.
An ellipse can be drawn by taking a piece of paper, two push-pins, a loop of string, and a pencil. The two pins are pushed through the paper into a suitable surface, providing the two foci for the ellipse. They should be closer together than the loop is long. The loop of string is placed around the base of these pins, leaving some slack. The pencil is now placed so that the pins and the loop form a triangle with a slight tension on the string.
Now try to draw a shape by moving the pencil about the pins while keeping the string taunt. The result should be an ellipse. The shape of the ellipse can be varied either by moving the pins closer together or further apart. This shape, according to Kepler, defines the path that a planet takes when it orbits the Sun.
|
| Kepler's First Law - A planet orbits the Sun on an ellipse with the Sun at one focus. |
Kepler's Second Law says in brief that an object speeds up as it gets closer to the Sun and slows down as it moves further away. Where the distance from the Sun to the orbital path is longer, only a smaller arc needs to be traversed to sweep out an area that requires a wider arc near the Sun.
As the planet moves closer to the Sun along its orbit the gravitational force works to increase the velocity. In contrast, as the planet is moving further away, the gravity of the Sun gradually decelerates the body and it is slowed down.

|
| Kepler's Second Law - A planet in orbit about the Sun sweeps out equal areas in the same time interval . |
A line that divides an ellipse in half and passes through the widest part of the ellipse is called the major axis. A line perpendicular to this axis and dividing the ellipse in half is called the minor axis. Half the length of the major axis is called the semi-major axis, and is represented by . The period required for a planet to complete one full orbit is represented by . The relationship between the period P and the length of the semimajor axis is known as Kepler's Third Law, and can be represented as follows:
where the symbol ∝ means "proportional to", and implies that there is a direct mathematical relationship between the period squared and the length of the semi-major axis cubed.
The Second and Third Laws provide a basis for calculating the period of any planet orbiting the Sun, as well as determining where the planet will be located along the orbital path.
Eccentricity and Orbital Paths
The ratio of the distance of a focus from the center of an ellipse to the semi-major axis is called the eccentricity of the orbit. When the two foci of the ellipse are on top of each other, the eccentricity is exactly 0.0 and the shape is a circle. As the eccentricity increases, the orbiting planet moves much further away than at the closest approach. The orbital eccentricities for planets in our Solar system vary from as much as 0.21 for Mercury down to 0.0068 for Venus.
The scientific name for the point of closest approach is the periapsis, while the most distance separation is the apoapsis. In the case of planets orbiting the Sun, these are called the perihelion and aphelion, respectively. (The -helion suffix comes from the Greek name for the Sun deity, Helios. This word is also the source of the name for the element Helium.)

|
| Two elliptical orbits with the same major axis but different eccentricity. |
Perhaps the most counter-intuitive aspect of the Third Law is that for any two identical bodies orbiting the Sun with the same semi-major axis, the orbital period is the same. This is true even if one is orbiting in a perfect circle and the other has an orbit that is highly elliptical (has a relatively high eccentricity). The elliptical shape will fit entirely within the circle except at two points (the ends of the major axis, at which the two curves will be tangent), so it is actually a shorter orbital path. However the aphelion of the ellipse will be located further from the Sun, so the planet will spend more time traversing the distant section of the orbit. The shorter orbit and the slower traverse of the aphelion compensate for each other, resulting in an identical period with the circular orbit.
Some Examples Using Kepler's Third Law
Originally, Kepler's Third Law was used to describe the motions of the planets around the Sun. As it turns out, it also works very well with regards to other two-body orbital systems like the orbits of moons around Jupiter, or the orbits of binary stars about the center of mass of their system. In all of these cases the period of the orbit squared is proportional to the length of the semi-major axis cubed, with the differences between the orbital systems reflected in the constant of proportionality.
In this section we will consider the special case of the planets going around the Sun. If we choose to measure the length of the semi-major axis of an orbit in astronomical units (abbreviated AU, where 1 AU is the distance from the Earth to the Sun) and we measure the orbital period in years (abbreviated as ), then we can express Kepler's Third Law as
where is measured in years and is measured in astronomical units. What follows are a few example of how to use this equation.
Mars' Orbital Period
Repeated measurements of Mars' orbit have determined that the semi-major axis of its orbit has a length of 1.52 AU. How long does it take for Mars to orbit the Sun once?
Solution: In this question, we are being asked for the orbital period of Mars. We know from reading the question that the length of the semi-major axis is 1.52 AU. Solving Kepler's Third Law for the period gives us
which tells us that it takes 1.87 years for Mars to go around the Sun once.
An Unknown Asteroid's Orbital Semi-Major Axis
An amateur astronomer spends several months tracking an asteroid and is able to determine that it takes approximately 3/4 of a year for it to orbit once around the Sun. What is the semi-major axis of this asteroid's orbit?
Solution: Reading the question tells us that the orbital period of the asteroid is 3/4 of a year, or 0.75 . We are expected to find the length of the semi-major axis , so we need to solve Kepler's Third Law for that. Doing so gives us
which means that is has a semi-major axis somewhere between that of Venus' orbit and Earth's orbit.
| General Astronomy | ||
| Observational Astronomy | Motion and Gravity | Principles of Light |












![{\displaystyle a=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{P^{2}}}=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{(0.75y)^{2}}}=0.83AU}](https://wikimedia.org/api/rest_v1/media/math/render/svg/286d7ac15ebe1b352620733947e5e0a279ba9de3)