Financial Math FM/Options
The basic trades of traded stock options (American style)[edit | edit source]
These trades are described from the point of view of a speculator. If they are combined with other positions, they can also be used in hedging. An option contract in US markets usually represents 100 shares of the underlying security.[1]
Long call[edit | edit source]

A trader who believes that a stock's price will increase might buy the right to purchase the stock, which is called a call option, rather than just purchase the stock itself. He would have no obligation to buy the stock, only the right to do so until the expiration date. If the stock price at expiration is above the exercise price by more than the premium (price) paid, he will profit. If the stock price at expiration is lower than the exercise price, he will let the call contract expire since it is worthless, and only lose the amount of the premium. A trader might buy the option instead of shares, because for the same amount of money, he can control a much larger number of shares.
Let Call(K,T) be the premium paid for a call option with strike price K and expiration time T, let be the stock price at time T and let i be the risk-free effective interest rate. The call option holder's profit per unit is
We can also write this as
- .
Long put[edit | edit source]
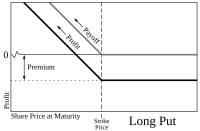
A trader who believes that a stock's price will decrease can buy the right to sell the stock at a fixed price a put option. He will be under no obligation to sell the stock, but has the right to do so until the expiration date. If the stock price at expiration is below the exercise price by more than the premium paid, he will profit. If the stock price at expiration is above the exercise price, he will let the put contract expire worthless and only lose the premium paid. The put option holder's profit per unit is
We can also write this as
- .
Short call[edit | edit source]

A trader who believes that a stock price will decrease, can sell the stock short or instead sell, or "write," a call. The trader selling a call has an obligation to sell the stock to the call buyer at the buyer's option. If the stock price decreases, the short call position will make a profit in the amount of the premium. If the stock price increases over the exercise price by more than the amount of the premium, the short will lose money, with the potential loss unlimited. The profit for the writer of a call option is
We can also write this as
- .
Short put[edit | edit source]

A trader who believes that a stock price will increase can buy the stock or instead sell, or "write", a put. The trader selling a put has an obligation to buy the stock from the put buyer at the put buyer's option. If the stock price at expiration is above the exercise price, the short put position will make a profit in the amount of the premium. If the stock price at expiration is below the exercise price by more than the amount of the premium, the trader will lose money, with the potential loss being up to the full value of the stock. A benchmark index for the performance of a cash-secured short put option position is the CBOE S&P 500 PutWrite Index (ticker PUT).
The profit for the writer of a put option is
We can also write this as
- .
Option Styles[edit | edit source]
European option[edit | edit source]
A European option may be exercised only at the expiry date of the option, i.e. at a single pre-defined point in time.
American option[edit | edit source]
An American option on the other hand may be exercised at any time before the expiry date.
Bermudan option[edit | edit source]
A Bermudan option is an option where the buyer has the right to exercise at a set (always discretely spaced) number of times. This is intermediate between a European option—which allows exercise at a single time, namely expiry—and an American option, which allows exercise at any time (the name is a pun: Bermuda is between America and Europe).
Value of an Option[edit | edit source]
ATM: At-the-money[edit | edit source]
An option is at-the-money if the strike price is the same as the spot price of the underlying security on which the option is written. An at-the-money option has no intrinsic value, only time value.
ITM: In-the-money[edit | edit source]
An in-the-money option has positive intrinsic value as well as time value. A call option is in-the-money when the strike price is below the spot price. A put option is in-the-money when the strike price is above the spot price.
OTM: Out-of-the-money[edit | edit source]
An out-of-the-money option has no intrinsic value. A call option is out-of-the-money when the strike price is above the spot price of the underlying security. A put option is out-of-the-money when the strike price is below the spot price.[1]
Example[edit | edit source]
Brian buys a call option on XYZ at a strike price of $10 a share. If on the expiration date the share price is $12 the option is In-the-money. Brian will exercise his option to buy at $10 a share. If the share price is $10 the option is At-the-money. Finally, if the share price is $8 his option is Out-of-the-money. He will not exercise his option which is now worthless.
Covered call[edit | edit source]

A covered call is a financial market transaction in which the seller of call options owns the corresponding amount of the underlying instrument, such as shares of a stock or other securities. If the trader buys the underlying instrument at the same time as he sells the call, the strategy is often called a "buy-write" strategy. In equilibrium, the strategy has the same payoffs as writing a put option.
Naked writing Dividends
Put-call parity[edit | edit source]
Call(K,T)-Put(K,T) = S_T - Ke^T
References[edit | edit source]
- ↑ invest-faq or Law & Valuation for typical size of option contract








