Data Structures/All Chapters
|
|
This work is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. In short: you are free to share and to make derivatives of this work under the conditions that you appropriately attribute it, and that you only distribute it under the same, similar or a compatible license. Any of the above conditions can be waived if you get permission from the copyright holder. |
Acknowledgment is given for using some contents from Wikipedia.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Computers can store and process vast amounts of data. Formal data structures enable a programmer to mentally structure large amounts of data into conceptually manageable relationships.
Sometimes we use data structures to allow us to do more: for example, to accomplish fast searching or sorting of data. Other times, we use data structures so that we can do less: for example, the concept of the stack is a limited form of a more general data structure. These limitations provide us with guarantees that allow us to reason about our programs more easily. Data structures also provide guarantees about algorithmic complexity — choosing an appropriate data structure for a job is crucial for writing good software.
Because data structures are higher-level abstractions, they present to us operations on groups of data, such as adding an item to a list, or looking up the highest-priority item in a queue. When a data structure provides operations, we can call the data structure an abstract data type (sometimes abbreviated as ADT). Abstract data types can minimize dependencies in your code, which is important when your code needs to be changed. Because you are abstracted away from lower-level details, some of the higher-level commonalities one data structure shares with a different data structure can be used to replace one with the other.
Our programming languages come equipped with a set of built-in types, such as integers and floating-point numbers, that allow us to work with data objects for which the machine's processor has native support. These built-in types are abstractions of what the processor actually provides because built-in types hide details both about their execution and limitations.
For example, when we use a floating-point number we are primarily concerned with its value and the operations that can be applied to it. Consider computing the length of a hypotenuse:
let c := sqrt(a * a + b * b)
The machine code generated from the above would use common patterns for computing these values and accumulating the result. In fact, these patterns are so repetitious that high-level languages were created to avoid this redundancy and to allow programmers to think about what value was computed instead of how it was computed.
Two useful and related concepts are at play here:
- Encapsulation is when common patterns are grouped together under a single name and then parameterized, in order to achieve a higher-level understanding of that pattern. For example, the multiplication operation requires two source values and writes the product of those two values to a given destination. The operation is parameterized by both the sources and the single destination.
- Abstraction is a mechanism to hide the implementation details of an abstraction away from the users of the abstraction. When we multiply numbers, for example, we don't need to know the technique actually used by the processor, we just need to know its properties.
A programming language is both an abstraction of a machine and a tool to encapsulate-away the machine's inner details. For example, a program written in a programming language can be compiled to several different machine architectures when that programming language sufficiently encapsulates the user away from any one machine.
In this book, we take the abstraction and encapsulation that our programming languages provide a step further: When applications get to be more complex, the abstractions of programming languages become too low-level to effectively manage. Thus, we build our own abstractions on top of these lower-level constructs. We can even build further abstractions on top of those abstractions. Each time we build upwards, we lose access to the lower-level implementation details. While losing such access might sound like a bad trade off, it is actually quite a bargain: We are primarily concerned with solving the problem at hand rather than with any trivial decisions that could have just as arbitrarily been replaced with a different decision. When we can think on higher levels, we relieve ourselves of these burdens.
Each data structure that we cover in this book can be thought of as a single unit that has a set of values and a set of operations that can be performed to either access or change these values. The data structure itself can be understood as a set of the data structure's operations together with each operation's properties (i.e., what the operation does and how long we could expect it to take).
Big-oh notation is a common way of expressing a computer code's performance. The notation creates a relationship between the number of items in memory and the average performance for a function. For a set of items, indicates that a particular function will operate on the set times on average. indicates that the function always performs a constant number of operations regardless of the number of items. The notation only represents algorithmic complexity so a function may perform more operations but constant multiples of are dropped by convention.
The Node[edit | edit source]
The first data structure we look at is the node structure. A node is simply a container for a value, plus a pointer to a "next" node (which may be null).
The above is an abstraction of a structure:
In some languages, structures are called records or classes. Some other languages provide no direct support for structures, but instead allow them to be built from other constructs (such as tuples or lists).
Here, we are only concerned that nodes contain values of some form, so we simply say its type is "element" because the type is not important. In some programming languages no type ever needs to be specified (as in dynamically typed languages, like Scheme, Smalltalk or Python). In other languages the type might need to be restricted to integer or string (as in statically typed languages like C). In still other languages, the decision of the type of the contained element can be delayed until the type is actually used (as in languages that support generic types, like C++ and Java). In any of these cases, translating the pseudocode into your own language should be relatively simple.
Each of the node operations specified can be implemented quite easily:
// Create a new node, with v as its contained value and next as
// the value of the next pointer
function make-node(v, node next): node
let result := new node {v, next}
return result
end
// Returns the value contained in node n
function get-value(node n): element
return n.value
end
// Returns the value of node n's next pointer
function get-next(node n): node
return n.next
end
// Sets the contained value of n to be v
function set-value(node n, v)
n.value := v
end
// Sets the value of node n's next pointer to be new-next
function set-next(node n, new-next)
n.next := new-next
return new-next
end
Principally, we are more concerned with the operations and the implementation strategy than we are with the structure itself and the low-level implementation. For example, we are more concerned about the time requirement specified, which states that all operations take time that is . The above implementation meets this criteria, because the length of time each operation takes is constant. Another way to think of constant time operations is to think of them as operations whose analysis is not dependent on any variable. (The notation is mathematically defined in the next chapter. For now, it is safe to assume it just means constant time.)
Because a node is just a container both for a value and container to a pointer to another node, it shouldn't be surprising how trivial the node data structure itself (and its implementation) is.
Building a Chain from Nodes[edit | edit source]
Although the node structure is simple, it actually allows us to compute things that we couldn't have computed with just fixed-size integers alone.
But first, we'll look at a program that doesn't need to use nodes. The following program will read in (from an input stream; which can either be from the user or a file) a series of numbers until the end-of-file is reached and then output what the largest number is and the average of all numbers:
program(input-stream in, output-stream out)
let total := 0
let count := 0
let largest :=
while has-next-integer(in):
let i := read-integer(in)
total := total + i
count := count + 1
largest := max(largest, i)
repeat
println out "Maximum: " largest
if count != 0:
println out "Average: " (total / count)
fi
end
But now consider solving a similar task: read in a series of numbers until the end-of-file is reached, and output the largest number and the average of all numbers that evenly divide the largest number. This problem is different because it's possible the largest number will be the last one entered: if we are to compute the average of all numbers that divide that number, we'll need to somehow remember all of them. We could use variables to remember the previous numbers, but variables would only help us solve the problem when there aren't too many numbers entered.
For example, suppose we were to give ourselves 200 variables to hold the state input by the user. And further suppose that each of the 200 variables had 64-bits. Even if we were very clever with our program, it could only compute results for different types of input. While this is a very large number of combinations, a list of 300 64-bit numbers would require even more combinations to be properly encoded. (In general, the problem is said to require linear space. All programs that need only a finite number of variables can be solved in constant space.)
Instead of building-in limitations that complicate coding (such as having only a constant number of variables), we can use the properties of the node abstraction to allow us to remember as many numbers as our computer can hold:
program(input-stream in, output-stream out)
let largest :=
let nodes := null
while has-next-integer(in):
let i := read-integer(in)
nodes := make-node(i, nodes) // contain the value i,
// and remember the previous numbers too
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
Above, if n integers are successfully read there will be n calls made to make-node. This will require n nodes to be made (which require enough space to hold the value and next fields of each node, plus internal memory management overhead), so the memory requirements will be on the order of . Similarly, we construct this chain of nodes and then iterate over the chain again, which will require steps to make the chain, and then another steps to iterate over it.
Note that when we iterate the numbers in the chain, we are actually looking at them in reverse order. For example, assume the numbers input to our program are 4, 7, 6, 30, and 15. After EOF is reached, the nodes chain will look like this:
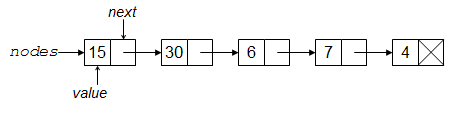
Such chains are more commonly referred to as linked-lists. However, we generally prefer to think in terms of lists or sequences, which aren't as low-level: the linking concept is just an implementation detail. While a list can be made with a chain, in this book we cover several other ways to make a list. For the moment, we care more about the abstraction capabilities of the node than we do about one of the ways it is used.
The above algorithm only uses the make-node, get-value, and get-next functions. If we use set-next we can change the algorithm to generate the chain so that it keeps the original ordering (instead of reversing it).
program (input-stream in, output-stream out)
let largest :=
let nodes := null
let tail_node := null
while has-next-integer (in):
let i := read-integer (in)
if (nodes == null)
nodes := make-node(i, null) // construct first node in the list
tail_node := nodes //there is one node in the list=> first and last are the same
else
tail_node := set-next (tail_node, make-node (i, null)) // append new node to the end of the list
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
The Principle of Induction[edit | edit source]
The chains we can build from nodes are a demonstration of the principle of mathematical induction:
Mathematical Induction
|
For example, let the property be the statement that "you can make a chain that holds numbers". This is a property of natural numbers, because the sentence makes sense for specific values of :
- you can make a chain that holds 5 numbers
- you can make a chain that holds 100 numbers
- you can make a chain that holds 1,000,000 numbers
Instead of proving that we can make chains of length 5, 100, and one million, we'd rather prove the general statement instead. Step 2 above is called the Inductive Hypothesis; let's show that we can prove it:
- Assume that holds. That is, that we can make a chain of elements. Now we must show that holds.
- Assume
chainis the first node of the -element chain. Assumeiis some number that we'd like to add to the chain to make an length chain. - The following code can accomplish this for us:
let bigger-chain := make-node(i, chain)
- Here, we have the new number
ithat is now the contained value of the first link of thebigger-chain. Ifchainhad elements, thenbigger-chainmust have elements.
Step 3 above is called the Base Case, let's show that we can prove it:
- We must show that holds. That is, that we can make a chain of one element.
- The following code can accomplish this for us:
let chain := make-node(i, null)
The principle of induction says, then, that we have proven that we can make a chain of elements for all value of . How is this so? Probably the best way to think of induction is that it's actually a way of creating a formula to describe an infinite number of proofs. After we prove that the statement is true for , the base case, we can apply the inductive hypothesis to that fact to show that holds. Since we now know that holds, we can apply the inductive hypothesis again to show that must hold. The principle says that there is nothing to stop us from doing this repeatedly, so we should assume it holds for all cases.
Induction may sound like a strange way to prove things, but it's a very useful technique. What makes the technique so useful is that it can take a hard sounding statement like "prove holds for all " and break it into two smaller, easier to prove statements. Typically base cases are easy to prove because they are not general statements at all. Most of the proof work is usually in the inductive hypothesis, which can often require clever ways of reformulating the statement to "attach on" a proof of the case.
You can think of the contained value of a node as a base case, while the next pointer of the node as the inductive hypothesis. Just as in mathematical induction, we can break the hard problem of storing an arbitrary number of elements into an easier problem of just storing one element and then having a mechanism to attach on further elements.
Induction on a Summation[edit | edit source]
The next example of induction we consider is more algebraic in nature:
Let's say we are given the formula and we want to prove that this formula gives us the sum of the first numbers. As a first attempt, we might try to just show that this is true for 1
- ,
for 2
- ,
for 3
and so on, however we'd quickly realize that our so called proof would take infinitely long to write out! Even if you carried out this proof and showed it to be true for the first billion numbers, that doesn't nescessarily mean that it would be true for one billion and one or even a hundred billion. This is a strong hint that maybe induction would be useful here.
Let's say we want to prove that the given formula really does give the sum of the first n numbers using induction. The first step is to prove the base case; i.e. we have to show that it is true when n = 1. This is relatively easy; we just substitute 1 for the variable n and we get (), which shows that the formula is correct when n = 1.
Now for the inductive step. We have to show that if the formula is true for j, it is also true for j + 1. To phrase it another way, assuming we've already proven that the sum from 1 to (j) is , we want to prove that the sum from 1 to (j+1) is . Note that those two formulas came about just by replacing n with (j) and (j+1) respectively.
To prove this inductive step, first note that to calculate the sum from 1 to j+1, you can just calculate the sum from 1 to j, then add j+1 to it. We already have a formula for the sum from 1 to j, and when we add j+1 to that formula, we get this new formula: . So to actually complete the proof, all we'd need to do is show that .
We can show the above equation is true via a few simplification steps:
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Asymptotic Notation[edit | edit source]
Introduction[edit | edit source]
There is no single data structure that offers optimal performance in every case. In order to choose the best structure for a particular task, we need to be able to judge how long a particular solution will take to run. Or, more accurately, you need to be able to judge how long two solutions will take to run, and choose the better of the two. We don't need to know how many minutes and seconds they will take, but we do need some way to compare algorithms against one another.
Asymptotic complexity is a way of expressing the main component of the cost of an algorithm, using idealized (not comparable) units of computational work. Consider, for example, the algorithm for sorting a deck of cards, which proceeds by repeatedly searching through the deck for the lowest card. The asymptotic complexity of this algorithm is the square of the number of cards in the deck. This quadratic behavior is the main term in the complexity formula, it says, e.g., if you double the size of the deck, then the work is roughly quadrupled.
The exact formula for the cost is more complex, and it contains more details than we need to understand the essential complexity of the algorithm. With our deck of cards, in the worst case, the deck would start out reverse-sorted, so our scans would have to go all the way to the end. The first scan would involve scanning cards, the next would take , etc. So the cost formula is . Generally, letting be the number of cards, the formula is , which equals . But the term dominates the expression, and this is what is key for comparing algorithm costs. (This is in fact an expensive algorithm; the best sorting algorithms run in sub-quadratic time.)
Asymptotically speaking, in the limit as tends towards infinity, gets closer and closer to the pure quadratic function . And what difference does the constant factor of make, at this level of abstraction? So the behavior is said to be .
Now let us consider how we would go about comparing the complexity of two algorithms. Let be the cost, in the worst case, of one algorithm, expressed as a function of the input size , and be the cost function for the other algorithm. E.g., for sorting algorithms, and would be the maximum number of steps that the algorithms would take on a list of items. If, for all values of , is less than or equal to , then the algorithm with complexity function is strictly faster. But, generally speaking, our concern for computational cost is for the cases with large inputs; so the comparison of and for small values of is less significant than the "long term" comparison of and , for larger than some threshold.
Note that we have been speaking about bounds on the performance of algorithms, rather than giving exact speeds. The actual number of steps required to sort our deck of cards (with our naive quadratic algorithm) will depend upon the order in which the cards begin. The actual time to perform each of our steps will depend upon our processor speed, the condition of our processor cache, etc., etc. It's all very complicated in the concrete details, and moreover not relevant to the essence of the algorithm.
The O Notation[edit | edit source]
Definition[edit | edit source]
The (pronounced big-oh) is the formal method of expressing the upper bound of an algorithm's running time. It's a measure of the longest amount of time it could possibly take for the algorithm to complete. We can assume that it represents the "worst case scenario" of a program.
More formally, for non-negative functions, and , if there exists an integer and a constant such that for all integers , , then is big O of . This is denoted as . If graphed, serves as an upper bound to the curve you are analyzing, .
Note that if can take on finite values only (as it should happen normally) then this definition implies that there exists some constant (potentially larger than ) such that for all values of , . An appropriate value for is the maximum of and .
Theory Examples[edit | edit source]
So, let's take an example of Big-O. Say that , and . Can we find a constant , so that ? The number works here, giving us . For any number greater than , this will still work. Since we're trying to generalize this for large values of , and small values aren't that important, we can say that is generally faster than ; that is, is bound by , and will always be less than it.
It could then be said that runs in time: "f-of-n runs in Big-O of n-squared time".
To find the upper bound - the Big-O time - assuming we know that is equal to (exactly) , we can take a few shortcuts. For example, we can remove all constants from the runtime; eventually, at some value of , they become irrelevant. This makes . Also, for convenience of comparison, we remove constant multipliers; in this case, the . This makes . It could also be said that runs in time; that lets us put a tighter (closer) upper bound onto the estimate.
Practical Examples[edit | edit source]
: printing a list of items to the screen, looking at each item once.
: taking a list of items, cutting it in half repeatedly until there's only one item left.
: taking a list of items, and comparing every item to every other item.
Big-Omega Notation[edit | edit source]
For non-negative functions, and , if there exists an integer and a constant such that for all integers , , then is . This is denoted as .
This is almost the same definition as Big Oh, except that , this makes a lower bound function, instead of an upper bound function. It describes the best that can happen for a given data size.
Theta Notation[edit | edit source]
For non-negative functions, and , is theta of if and only if and . This is denoted as .
This is basically saying that the function, is bounded both from the top and bottom by the same function, .
The theta notation is denoted by Q.
Little-O Notation[edit | edit source]
For non-negative functions, and , is little o of if and only if , but . This is denoted as .
This represents a loose bounding version of Big O. bounds from the top, but it does not bound the bottom.
Little Omega Notation[edit | edit source]
For non-negative functions, and , is little omega of if and only if , but . This is denoted as .
Much like Little Oh, this is the equivalent for Big Omega. is a loose lower boundary of the function ; it bounds from the bottom, but not from the top.
How asymptotic notation relates to analyzing complexity[edit | edit source]
Temporal comparison is not the only issue in algorithms. There are space issues as well. Generally, a trade off between time and space is noticed in algorithms. Asymptotic notation empowers you to make that trade off. If you think of the amount of time and space your algorithm uses as a function of your data over time or space (time and space are usually analyzed separately), you can analyze how the time and space is handled when you introduce more data to your program.
This is important in data structures because you want a structure that behaves efficiently as you increase the amount of data it handles. Keep in mind though that algorithms that are efficient with large amounts of data are not always simple and efficient for small amounts of data. So if you know you are working with only a small amount of data and you have concerns for speed and code space, a trade off can be made for a function that does not behave well for large amounts of data.
A few examples of asymptotic notation[edit | edit source]
Generally, we use asymptotic notation as a convenient way to examine what can happen in a function in the worst case or in the best case. For example, if you want to write a function that searches through an array of numbers and returns the smallest one:
function find-min(array a[1..n])
let j :=
for i := 1 to n:
j := min(j, a[i])
repeat
return j
end
Regardless of how big or small the array is, every time we run find-min, we have to initialize the i and j integer variables and return j at the end. Therefore, we can just think of those parts of the function as constant and ignore them.
So, how can we use asymptotic notation to discuss the find-min function? If we search through an array with 87 elements, then the for loop iterates 87 times, even if the very first element we hit turns out to be the minimum. Likewise, for elements, the for loop iterates times. Therefore we say the function runs in time .
What about this function:
function find-min-plus-max(array a[1..n]) // First, find the smallest element in the array let j := ; for i := 1 to n: j := min(j, a[i]) repeat let minim := j // Now, find the biggest element, add it to the smallest and j := ; for i := 1 to n: j := max(j, a[i]) repeat let maxim := j // return the sum of the two return minim + maxim; end
What's the running time for find-min-plus-max? There are two for loops, that each iterate times, so the running time is clearly . Because is a constant, we throw it away and write the running time as . Why can you do this? If you recall the definition of Big-O notation, the function whose bound you're testing can be multiplied by some constant. If , we can see that if , then the Big-O condition holds. Thus . This rule is general for the various asymptotic notations.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
| |
A Wikibookian has nominated this page for cleanup. You can help make it better. Please review any relevant discussion. |
| A Wikibookian has nominated this page for cleanup. You can help make it better. Please review any relevant discussion. |
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Arrays[edit | edit source]
An array is a collection, mainly of similar data types, stored into a common variable. The collection forms a data structure where objects are stored linearly, one after another in memory. Sometimes arrays are even replicated into the memory hardware.
The structure can also be defined as a particular method of storing elements of indexed data. Elements of data are logically stored sequentially in blocks within the array. Each element is referenced by an index, or subscripts.
The index is usually a number used to address an element in the array. For example, if you were storing information about each day in August, you would create an array with an index capable of addressing 31 values—one for each day of the month. Indexing rules are language dependent, however most languages use either 0 or 1 as the first element of an array.
The concept of an array can be daunting to the uninitiated, but it is really quite simple. Think of a notebook with pages numbered 1 through 12. Each page may or may not contain information on it. The notebook is an array of pages. Each page is an element of the array 'notebook'. Programmatically, you would retrieve information from a page by referring to its number or subscript, i.e., notebook(4) would refer to the contents of page 4 of the array notebook.
The notebook (array) contains 12 pages (elements)
Arrays can also be multidimensional - instead of accessing an element of a one-dimensional list, elements are accessed by two or more indices, as from a matrix or tensor.
Multidimensional arrays are as simple as our notebook example above. To envision a multidimensional array, think of a calendar. Each page of the calendar, 1 through 12, is an element, representing a month, which contains approximately 30 elements, which represent days. Each day may or may not have information in it. Programmatically then, calendar(4,15) would refer to the 4th month, 15th day. Thus we have a two-dimensional array. To envision a three-dimensional array, break each day up into 24 hours. Now calendar(4,15,9) would refer to 4th month, 15th day, 9th hour.

A simple 6 element by 4 element array
Array<Element> Operations
make-array(integer n): Array
- Create an array of elements indexed from to , inclusive. The number of elements in the array, also known as the size of the array, is n.
get-value-at(Array a, integer index): Element
- Returns the value of the element at the given index. The value of index must be in bounds: 0 <= index <= (n - 1). This operation is also known as subscripting.
set-value-at(Array a, integer index, Element new-value)
- Sets the element of the array at the given index to be equal to new-value.
Arrays guarantee constant time read and write access, , however many lookup operations (find_min, find_max, find_index) of an instance of an element are linear time, . Arrays are very efficient in most languages, as operations compute the address of an element via a simple formula based on the base address element of the array.
Array implementations differ greatly between languages: some languages allow arrays to be re-sized automatically, or to even contain elements of differing types (such as Perl). Other languages are very strict and require the type and length information of an array to be known at run time (such as C).
Arrays typically map directly to contiguous storage locations within your computer's memory and are therefore the "natural" storage structure for most higher level languages.
Simple linear arrays are the basis for most of the other data structures. Many languages do not allow you to allocate any structure except an array, everything else must be implemented on top of the array. The exception is the linked list, that is typically implemented as individually allocated objects, but it is possible to implement a linked list within an array.
Type[edit | edit source]
The array index needs to be of some type. Usually, the standard integer type of that language is used, but there are also languages such as Ada and Pascal which allow any discrete type as an array index. Scripting languages often allow any type as an index (associative array).
Bounds[edit | edit source]
The array index consists of a range of values with a lower bound and an upper bound.
In some programming languages only the upper bound can be chosen while the lower bound is fixed to be either 0 (C, C++, C#, Java) or 1 (FORTRAN 66, R).
In other programming languages (Ada, PL/I, Pascal) both the upper and lower bound can be freely chosen (even negative).
Bounds check[edit | edit source]
The third aspect of an array index is the check for valid ranges and what happens when an invalid index is accessed. This is a very important point since the majority of computer worms and computer viruses attack by using invalid array bounds.
There are three options open:
- Most languages (Ada, PL/I, Pascal, Java, C#) will check the bounds and raise some error condition when an element is accessed which does not exist.
- A few languages (C, C++) will not check the bounds and return or set some arbitrary value when an element outside the valid range is accessed.
- Scripting languages often automatically expand the array when data is written to an index which was not valid until then.
Declaring Array Types[edit | edit source]
The declaration of array type depends on how many features the array in a particular language has.
The easiest declaration is when the language has a fixed lower bound and fixed index type. If you need an array to store the monthly income you could declare in C
typedef double Income[12];
This gives you an array with in the range of 0 to 11. For a full description of arrays in C see C Programming/Arrays.
If you use a language where you can choose both the lower bound as well as the index type, the declaration is—of course—more complex. Here are two examples in Ada:
type Month is range 1 .. 12;
type Income is array(Month) of Float;
or shorter:
type Income is array(1 .. 12) of Float;
For a full description of arrays in Ada see Ada Programming/Types/array.
Array Access[edit | edit source]
We generally write arrays with a name, followed by the index in some brackets, square '[]' or round '()'. For example, August[3] is the method used in the C programming language to refer to a particular day in the month.
Because the C language starts the index at zero, August[3] is the 4th element in the array. august[0] actually refers to the first element of this array. Starting an index at zero is natural for computers, whose internal representations of numbers begin with zero, but for humans, this unnatural numbering system can lead to problems when accessing data in an array. When fetching an element in a language with zero-based indexes, keep in mind the true length of an array, lest you find yourself fetching the wrong data. This is the disadvantage of programming in languages with fixed lower bounds, the programmer must always remember that "[0]" means "1st" and, when appropriate, add or subtract one from the index. Languages with variable lower bounds will take that burden off the programmer's shoulder.
We use indexes to store related data. If our C language array is called august, and we wish to store that we're going to the supermarket on the 1st, we can say, for example
august[0] = "Going to the shops today"
In this way, we can go through the indexes from 0 to 30 and get the related tasks for each day in august.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
List Structures and Iterators[edit | edit source]
We have now seen two different data structures that allow us to store an ordered sequence of elements. However, they have two very different interfaces. The array allows us to use get-element() and set-element() functions to access and change elements. The node chain requires us to use get-next() until we find the desired node, and then we can use get-value() and set-value() to access and modify its value. Now, what if you've written some code, and you realize that you should have been using the other sequence data structure? You have to go through all of the code you've already written and change one set of accessor functions into another. What a pain! Fortunately, there is a way to localize this change into only one place: by using the List Abstract Data Type (ADT).
List<item-type> ADT
get-begin():List Iterator<item-type>- Returns the list iterator (we'll define this soon) that represents the first element of the list. Runs in time.
get-end():List Iterator<item-type>- Returns the list iterator that represents one element past the last element in the list. Runs in time.
prepend(new-item:item-type)- Adds a new element at the beginning of a list. Runs in time.
insert-after(iter:List Iterator<item-type>, new-item:item-type)- Adds a new element immediately after iter. Runs in time.
remove-first()- Removes the element at the beginning of a list. Runs in time.
remove-after(iter:List Iterator<item-type>)- Removes the element immediately after iter. Runs in time.
is-empty():Boolean- True if there are no elements in the list. Has a default implementation. Runs in time.
get-size():Integer- Returns the number of elements in the list. Has a default implementation. Runs in time.
get-nth(n:Integer):item-type- Returns the nth element in the list, counting from 0. Has a default implementation. Runs in time.
set-nth(n:Integer, new-value:item-type)- Assigns a new value to the nth element in the list, counting from 0. Has a default implementation. Runs in time.
The iterator is another abstraction that encapsulates both access to a single element and incremental movement around the list. Its interface is very similar to the node interface presented in the introduction, but since it is an abstract type, different lists can implement it differently.
List Iterator<item-type> ADT
get-value():item-type- Returns the value of the list element that this iterator refers to.
set-value(new-value:item-type)- Assigns a new value to the list element that this iterator refers to.
move-next()- Makes this iterator refer to the next element in the list.
equal(other-iter:List Iterator<item-type>):Boolean- True if the other iterator refers to the same list element as this iterator.
All operations run in time.
There are several other aspects of the List ADT's definition that need more explanation. First, notice that the get-end() operation returns an iterator that is "one past the end" of the list. This makes its implementation a little trickier, but allows you to write loops like:
var iter:List Iterator := list.get-begin() while(not iter.equal(list.get-end())) # Do stuff with the iterator iter.move-next() end while
Second, each operation gives a worst-case running time. Any implementation of the List ADT is guaranteed to be able to run this operation at least that fast. Most implementations will run most of the operations faster. For example, the node chain implementation of List can run insert-after() in .
Third, some of the operations say that they have a default implementation. This means that these operations can be implemented in terms of other, more primitive operations. They're included in the ADT so that certain implementations can implement them faster. For example, the default implementation of get-nth() runs in because it has to traverse all of the elements before the nth. Yet the array implementation of List can implement it in using its get-element() operation. The other default implementations are:
abstract type List<item-type> method is-empty() return get-begin().equal(get-end()) end method method get-size():Integer var size:Integer := 0 var iter:List Iterator<item-type> := get-begin() while(not iter.equal(get-end())) size := size+1 iter.move-next() end while return size end method helper method find-nth(n:Integer):List Iterator<item-type> if n >= get-size() error "The index is past the end of the list" end if var iter:List Iterator<item-type> := get-begin() while(n > 0) iter.move-next() n := n-1 end while return iter end method method get-nth(n:Integer):item-type return find-nth(n).get-value() end method method set-nth(n:Integer, new-value:item-type) find-nth(n).set-value(new-value) end method end type
Syntactic Sugar[edit | edit source]
Occasionally throughout this book we'll introduce an abbreviation that will allow us to write, and you to read, less pseudocode. For now, we'll introduce an easier way to compare iterators and a specialized loop for traversing sequences.
Instead of using the equal() method to compare iterators, we'll overload the == operator. To be precise, the following two expressions are equivalent:
iter1.equal(iter2) iter1 == iter2
Second, we'll use the for keyword to express list traversal. The following two blocks are equivalent:
var iter:List Iterator<item-type> := list.get-begin() while(not iter == list.get-end()) operations on iter iter.move-next() end while
for iter in list operations on iter end for
Implementations[edit | edit source]
In order to actually use the List ADT, we need to write a concrete data type that implements its interface. There are two standard data types that naturally implement List: the node chain described in the Introduction, normally called a Singly Linked List; and an extension of the array type called a Vector, which automatically resizes itself to accommodate inserted nodes.
Singly Linked List[edit | edit source]
type Singly Linked List<item-type> implements List<item-type>
head refers to the first node in the list. When it's null, the list is empty.
data head:Node<item-type>
Initially, the list is empty.
constructor()
head := null
end constructor
method get-begin():Sll Iterator<item-type>
return new Sll-Iterator(head)
end method
The "one past the end" iterator is just a null node. To see why, think about what you get when you have an iterator for the last element in the list and you call move-next().
method get-end():Sll Iterator<item-type>
return new Sll-Iterator(null)
end method
method prepend(new-item:item-type)
head = make-node(new-item, head)
end method
method insert-after(iter:Sll Iterator<item-type>, new-item:item-type)
var new-node:Node<item-type> := make-node(new-item, iter.node().get-next())
iter.node.set-next(new-node)
end method
method remove-first()
head = head.get-next()
end method
This takes the node the iterator holds and makes it point to the node two nodes later.
method remove-after(iter:Sll Iterator<item-type>)
iter.node.set-next(iter.node.get-next().get-next())
end method
end type
If we want to make get-size() be an operation, we can add an Integer data member that keeps track of the list's size at all times. Otherwise, the default implementation works fine.
An iterator for a singly linked list simply consists of a reference to a node.
type Sll Iterator<item-type>
data node:Node<item-type>
constructor(_node:Node<item-type>)
node := _node
end constructor
Most of the operations just pass through to the node.
method get-value():item-type
return node.get-value()
end method
method set-value(new-value:item-type)
node.set-value(new-value)
end method
method move-next()
node := node.get-next()
end method
For equality testing, we assume that the underlying system knows how to compare nodes for equality. In nearly all languages, this would be a pointer comparison.
method equal(other-iter:List Iterator<item-type>):Boolean
return node == other-iter.node
end method
end type
Vector[edit | edit source]
Let's write the Vector's iterator first. It will make the Vector's implementation clearer.
type Vector Iterator<item-type>
data array:Array<item-type>
data index:Integer
constructor(my_array:Array<item-type>, my_index:Integer)
array := my_array
index := my_index
end constructor
method get-value():item-type
return array.get-element(index)
end method
method set-value(new-value:item-type)
array.set-element(index, new-value)
end method
method move-next()
index := index+1
end method
method equal(other-iter:List Iterator<item-type>):Boolean
return array==other-iter.array and index==other-iter.index
end method
end type
We implement the Vector in terms of the primitive Array data type. It is inefficient to always keep the array exactly the right size (think of how much resizing you'd have to do), so we store both a size, the number of logical elements in the Vector, and a capacity, the number of spaces in the array. The array's valid indices will always range from 0 to capacity-1.
type Vector<item-type> data array:Array<item-type> data size:Integer data capacity:Integer
We initialize the vector with a capacity of 10. Choosing 10 was fairly arbitrary. If we'd wanted to make it appear less arbitrary, we would have chosen a power of 2, and innocent readers like you would assume that there was some deep, binary-related reason for the choice.
constructor()
array := create-array(0, 9)
size := 0
capacity := 10
end constructor
method get-begin():Vector-Iterator<item-type>
return new Vector-Iterator(array, 0)
end method
The end iterator has an index of size. That's one more than the highest valid index.
method get-end():List Iterator<item-type>
return new Vector-Iterator(array, size)
end method
We'll use this method to help us implement the insertion routines. After it is called, the capacity of the array is guaranteed to be at least new-capacity. A naive implementation would simply allocate a new array with exactly new-capacity elements and copy the old array over. To see why this is inefficient, think what would happen if we started appending elements in a loop. Once we exceeded the original capacity, each new element would require us to copy the entire array. That's why this implementation at least doubles the size of the underlying array any time it needs to grow.
helper method ensure-capacity(new-capacity:Integer)
If the current capacity is already big enough, return quickly.
if capacity >= new-capacity
return
end if
Now, find the new capacity we'll need,
var allocated-capacity:Integer := max(capacity*2, new-capacity)
var new-array:Array<item-type> := create-array(0, allocated-capacity - 1)
copy over the old array,
for i in 0..size-1
new-array.set-element(i, array.get-element(i))
end for
and update the Vector's state.
array := new-array
capacity := allocated-capacity
end method
This method uses a normally-illegal iterator, which refers to the item one before the start of the Vector, to trick insert-after() into doing the right thing. By doing this, we avoid duplicating code.
method prepend(new-item:item-type)
insert-after(new Vector-Iterator(array, -1), new-item)
end method
insert-after() needs to copy all of the elements between iter and the end of the Vector. This means that in general, it runs in time. However, in the special case where iter refers to the last element in the vector, we don't need to copy any elements to make room for the new one. An append operation can run in time, plus the time needed for the ensure-capacity() call. ensure-capacity() will sometimes need to copy the whole array, which takes time. But much more often, it doesn't need to do anything at all.
Amortized Analysis
In fact, if you think of a series of append operations starting immediately after ensure-capacity() increases the Vector's capacity (call the capacity here ), and ending immediately after the next increase in capacity, you can see that there will be exactly appends. At the later increase in capacity, it will need to copy elements over to the new array. So this entire sequence of function calls took operations. We call this situation, where there are operations for function calls "amortized time".
method insert-after(iter:Vector Iterator<item-type>, new-item:item-type)
ensure-capacity(size+1)
This loop copies all of the elements in the vector into the spot one index up. We loop backwards in order to make room for each successive element just before we copy it.
for i in size-1 .. iter.index+1 step -1
array.set-element(i+1, array.get-element(i))
end for
Now that there is an empty space in the middle of the array, we can put the new element there.
array.set-element(iter.index+1, new-item)
And update the Vector's size.
size := size+1 end method
Again, cheats a little bit to avoid duplicate code.
method remove-first() remove-after(new Vector-Iterator(array, -1)) end method
Like insert-after(), remove-after needs to copy all of the elements between iter and the end of the Vector. So in general, it runs in time. But in the special case where iter refers to the last element in the vector, we can simply decrement the Vector's size, without copying any elements. A remove-last operation runs in time.
method remove-after(iter:List Iterator<item-type>)
for i in iter.index+1 .. size-2
array.set-element(i, array.get-element(i+1))
end for
size := size-1
end method
This method has a default implementation, but we're already storing the size, so we can implement it in time, rather than the default's
method get-size():Integer
return size
end method
Because an array allows constant-time access to elements, we can implement get- and set-nth() in , rather than the default implementation's
method get-nth(n:Integer):item-type
return array.get-element(n)
end method
method set-nth(n:Integer, new-value:item-type)
array.set-element(n, new-value)
end method
end type
Bidirectional Lists[edit | edit source]
Sometimes we want Data Structures/All Chapters to move backward in a list too. A Bidirectional List allows the list to be searched forwards and backwards. A Bidirectional list implements an additional iterator function, move-previous().
Bidirectional List<item-type> ADT
get-begin():Bidirectional List Iterator<item-type>- Returns the list iterator (we'll define this soon) that represents the first element of the list. Runs in time.
get-end():Bidirectional List Iterator<item-type>- Returns the list iterator that represents one element past the last element in the list. Runs in time.
insert(iter:Bidirectional List Iterator<item-type>, new-item:item-type)- Adds a new element immediately before iter. Runs in time.
remove(iter:Bidirectional List Iterator<item-type>)- Removes the element immediately referred to by iter. After this call, iter will refer to the next element in the list. Runs in time.
is-empty():Boolean- True iff there are no elements in the list. Has a default implementation. Runs in time.
get-size():Integer- Returns the number of elements in the list. Has a default implementation. Runs in time.
get-nth(n:Integer):item-type- Returns the nth element in the list, counting from 0. Has a default implementation. Runs in time.
set-nth(n:Integer, new-value:item-type)- Assigns a new value to the nth element in the list, counting from 0. Has a default implementation. Runs in time.
Bidirectional List Iterator<item-type> ADT
get-value():item-type- Returns the value of the list element that this iterator refers to. Undefined if the iterator is past-the-end.
set-value(new-value:item-type)- Assigns a new value to the list element that this iterator refers to. Undefined if the iterator is past-the-end.
move-next()- Makes this iterator refer to the next element in the list. Undefined if the iterator is past-the-end.
move-previous()- Makes this iterator refer to the previous element in the list. Undefined if the iterator refers to the first list element.
equal(other-iter:List Iterator<item-type>):Boolean- True iff the other iterator refers to the same list element as this iterator.
All operations run in time.
Doubly Linked List Implementation[edit | edit source]
Vector Implementation[edit | edit source]
The vector we've already seen has a perfectly adequate implementation to be a Bidirectional List. All we need to do is add the extra member functions to it and its iterator; the old ones don't have to change.
type Vector<item-type> ... # already-existing data and methods
Implement this in terms of the original insert-after() method. After that runs, we have to adjust iter's index so that it still refers to the same element.
method insert(iter:Bidirectional List Iterator<item-type>, new-item:item-type)
insert-after(new Vector-Iterator(iter.array, iter.index-1))
iter.move-next()
end method
Also implement this on in terms of an old function. After remove-after() runs, the index will already be correct.
method remove(iter:Bidirectional List Iterator<item-type>)
remove-after(new Vector-Iterator(iter.array, iter.index-1))
end method
end type
Tradeoffs[edit | edit source]
In order to choose the correct data structure for the job, we need to have some idea of what we're going to *do* with the data.
- Do we know that we'll never have more than 100 pieces of data at any one time, or do we need to occasionally handle gigabytes of data ?
- How will we read the data out ? Always in chronological order ? Always sorted by name ? Randomly accessed by record number ?
- Will we always add/delete data to the end or to the beginning ? Or will we be doing a lot of insertions and deletions in the middle ?
We must strike a balance between the various requirements. If we need to frequently read data out in 3 different ways, pick a data structure that allows us to do all 3 things not-too-slowly. Don't pick some data structure that's unbearably slow for *one* way, no matter how blazingly fast it is for the other ways.
Often the shortest, simplest programming solution for some task will use a linear (1D) array.
If we keep our data as an ADT, that makes it easier to temporarily switch to some other underlying data structure, and objectively measure whether it's faster or slower.
Advantages / Disadvantages[edit | edit source]
For the most part, an advantage of an array is a disadvantage of a linked list, and vice versa.
- Array Advantages (vs. Linked Lists)
- Index - Indexed access to any element in an array is fast; a linked list must be traversed from the beginning to reach the desired element.
- Faster - In general, accessing an element in an array is faster than accessing an element in a linked list.
- Linked-List Advantages (vs. Arrays)
- Resize - A linked list can easily be resized by adding elements without affecting the other elements in the list; an array can be enlarged only by allocating new chunk of memory and copying all the elements.
- Insertion - An element can easily be inserted into the middle of a linked list: a new link is created with a pointer to the link after it, and the previous link is made to point to the new link.
Side-note: - How to insert an element in the middle of an array. If an array is not full, you take all the elements after the spot or index in the array you want to insert, and move them forward by 1, then insert your element. If the array is already full and you want to insert an element, you would have to, in a sense, 'resize the array.' A new array would have to be made one size larger than the original array to insert your element, then all the elements of the original array are copied to the new array taking into consideration the spot or index to insert your element, then insert your element.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Stacks and Queues[edit | edit source]
Stacks[edit | edit source]
A stack is a basic data structure that can be logically thought of as a linear structure represented by a real physical stack or pile, a structure where insertion and deletion of items takes place at one end called top of the stack. The basic concept can be illustrated by thinking of your data set as a stack of plates or books where you can only take the top item of the stack in order to remove things from it. This structure is used all throughout programming.
The basic implementation of a stack is also called a LIFO (Last In First Out) to demonstrate the way it accesses data, since as we will see there are various variations of stack implementations.
There are basically three operations that can be performed on stacks. They are 1) inserting an item into a stack (push). 2) deleting an item from the stack (pop). 3) displaying the contents of the stack (peek or top).
Below are some of operations a stack data type normally supports:
Stack<item-type> Operations
push(new-item:item-type)- Adds an item onto the stack.
top():item-type- Returns the last item pushed onto the stack.
pop()- Removes the most-recently-pushed item from the stack.
is-empty():Boolean- True if no more items can be popped and there is no top item.
is-full():Boolean- True if no more items can be pushed.
get-size():Integer- Returns the number of elements on the stack.
All operations except get-size() can be performed in time. get-size() runs in at worst
Linked List Implementation[edit | edit source]
The basic linked list implementation is one of the easiest stack implementations you can do. Structurally it is a linked list.
type Stack<item_type>
data list:Singly Linked List<item_type>
"stack follows the LIFO (last in first out) operation"
"queue follows the FIFO (first in first out) operation"
constructor()
list := new Singly-Linked-List()
end constructor
Most operations are implemented by passing them through to the underlying linked list. When you want to push something onto the list, you simply add it to the front of the linked list. The previous top is then "next" from the item being added and the list's front pointer points to the new item.
method push(new_item:item_type)
list.prepend(new_item)
end method
To look at the top item, you just examine the first item in the linked list.
method top():item_type
return list.get-begin().get-value()
end method
When you want to pop something off the list, simply remove the first item from the linked list.
method pop()
list.remove-first()
end method
A check for emptiness is easy. Just check if the list is empty.
method is-empty():Boolean
return list.is-empty()
end method
A check for full is simple. Linked lists are considered to be limitless in size.
method is-full():Boolean
return False
end method
A check for the size is again passed through to the list.
method get-size():Integer
return list.get-size()
end method
end type
A real Stack implementation in a published library would probably re-implement the linked list in order to squeeze the last bit of performance out of the implementation by leaving out unneeded functionality. The above implementation gives you the ideas involved, and any optimization you need can be accomplished by inlining the linked list code.
Performance Analysis[edit | edit source]
In a linked list, accessing the first element is an operation.The list contains a pointer that checks for empty/fullness as done here are also
(depending on what time/space tradeoff is made). Most of the time, users of a Stack do not use the getSize() operation, and so a bit of space can be saved by not optimizing it.
Since all operations are at the top of the stack, the array implementation is now much, much better.
public class StackArray implements Stack
{
protected int top;
protected Object[] data;
...
}
The array implementation keeps the bottom of the stack at the beginning of the array. It grows toward the end of the array. The only problem is if you attempt to push an element when the array is full. If so
Assert.pre(!isFull(),"Stack is not full.");
will fail, raising an exception. Thus it makes more sense to implement with Vector (see StackVector) to allow unbounded growth (at cost of occasional O(n) delays).
Complexity:
All operations are O(1) with exception of occasional push and clear, which should replace all entries by null in order to let them be garbage-collected. Array implementation does not replace null entries. The Vector implementation does...
Applications of Stacks[edit | edit source]

Using stacks, we can solve many applications, some of which are listed below.
Converting a decimal number into a binary number[edit | edit source]
The logic for transforming a decimal number into a binary number is as follows:
* Read a number
* Iteration (while number is greater than zero)
1. Find out the remainder after dividing the number by 2
2. Print the remainder
3. Divide the number by 2
* End the iteration
However, there is a problem with this logic. Suppose the number whose binary form we want to find is 23. Using this logic, we get the result as 11101, instead of getting 10111.
To solve this problem, we use a stack. We make use of the LIFO property of the stack. Initially we push the binary digit formed into the stack, instead of printing it directly. After the entire digit has been converted into the binary form, we pop one digit at a time from the stack and print it. Therefore we get the decimal number is converted into its proper binary form.
Algorithm:
1. Create a stack
2. Enter a decimal number which has to be converted into its equivalent binary form.
3. iteration1 (while number > 0)
3.1 digit = number % 2
3.2 Push digit into the stack
3.3 If the stack is full
3.3.1 Print an error
3.3.2 Stop the algorithm
3.4 End the if condition
3.5 Divide the number by 2
4. End iteration1
5. iteration2 (while stack is not empty)
5.1 Pop digit from the stack
5.2 Print the digit
6. End iteration2
7. STOP
Towers of Hanoi[edit | edit source]

One of the most interesting applications of stacks can be found in solving a puzzle called Tower of Hanoi. According to an old Brahmin story, the existence of the universe is calculated in terms of the time taken by a number of monks, who are working all the time, to move 64 disks from one pole to another. But there are some rules about how this should be done, which are:
- You can move only one disk at a time.
- For temporary storage, a third pole may be used.
- You cannot place a disk of larger diameter on a disk of smaller diameter.[1]
Here we assume that A is first tower, B is second tower & C is third tower.





Output : (when there are 3 disks)
Let 1 be the smallest disk, 2 be the disk of medium size and 3 be the largest disk.
| Move disk | From peg | To peg |
|---|---|---|
| 1 | A | C |
| 2 | A | B |
| 1 | C | B |
| 3 | A | C |
| 1 | B | A |
| 2 | B | C |
| 1 | A | C |
Output : (when there are 4 disks)
| Move disk | From peg | To peg |
|---|---|---|
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
| 3 | A | B |
| 1 | C | A |
| 2 | C | B |
| 1 | A | B |
| 4 | A | C |
| 1 | B | C |
| 2 | B | A |
| 1 | C | A |
| 3 | B | C |
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
The C++ code for this solution can be implemented in two ways:
First Implementation (Without using Stacks)[edit | edit source]
Here we assume that A is first tower, B is second tower & C is third tower. (B is the intermediate)
void TowersofHanoi(int n, int a, int b, int c)
{
//Move top n disks from tower a to tower b, use tower c for intermediate storage.
if(n > 0)
{
TowersofHanoi(n-1, a, c, b); //recursion
cout << " Move top disk from tower " << a << " to tower " << b << endl ;
//Move n-1 disks from intermediate(b) to the source(a) back
TowersofHanoi(n-1, c, b, a); //recursion
}
}
Second Implementation (Using Stacks)[edit | edit source]
// Global variable, tower [1:3] are three towers
arrayStack<int> tower[4];
void TowerofHanoi(int n)
{
// Preprocessor for moveAndShow.
for (int d = n; d > 0; d--) //initialize
tower[1].push(d); //add disk d to tower 1
moveAndShow(n, 1, 2, 3); /*move n disks from tower 1 to tower 3 using
tower 2 as intermediate tower*/
}
void moveAndShow(int n, int a, int b, int c)
{
// Move the top n disks from tower a to tower b showing states.
// Use tower c for intermediate storage.
if(n > 0)
{
moveAndShow(n-1, a, c, b); //recursion
int d = tower[a].top(); //move a disc from top of tower a to top of
tower[a].pop(); //tower b
tower[b].push(d);
showState(); //show state of 3 towers
moveAndShow(n-1, c, b, a); //recursion
}
}
However complexity for above written implementations is O(). So it's obvious that problem can only be solved for small values of n (generally n <= 30). In case of the monks, the number of turns taken to transfer 64 disks, by following the above rules, will be 18,446,744,073,709,551,615; which will surely take a lot of time!!
Expression evaluation and syntax parsing[edit | edit source]
Calculators employing reverse Polish notation use a stack structure to hold values. Expressions can be represented in prefix, postfix or infix notations. Conversion from one form of the expression to another form may be accomplished using a stack. Many compilers use a stack for parsing the syntax of expressions, program blocks etc. before translating into low level code. Most of the programming languages are context-free languages allowing them to be parsed with stack based machines.
Evaluation of an Infix Expression that is Fully Parenthesized[edit | edit source]
Input: (((2 * 5) - (1 * 2)) / (9 - 7))
Output: 4
Analysis: Five types of input characters
* Opening bracket * Numbers * Operators * Closing bracket * New line character
Data structure requirement: A character stack
Algorithm
1. Read one input character
2. Actions at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Push into stack and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from character stack
(2.4.1) if it is opening bracket, then discard it, Go to step (1)
(2.4.2) Pop is used three times
The first popped element is assigned to op2
The second popped element is assigned to op
The third popped element is assigned to op1
Evaluate op1 op op2
Convert the result into character and
push into the stack
Go to step (2.4)
New line character (2.5) Pop from stack and print the answer
STOP
Result: The evaluation of the fully parenthesized infix expression is printed on the monitor as follows:
Input String: (((2 * 5) - (1 * 2)) / (9 - 7))
| Input Symbol | Stack (from bottom to top) | Operation |
|---|---|---|
| ( | ( | |
| ( | ( ( | |
| ( | ( ( ( | |
| 2 | ( ( ( 2 | |
| * | ( ( ( 2 * | |
| 5 | ( ( ( 2 * 5 | |
| ) | ( ( 10 | 2 * 5 = 10 & Push |
| - | ( ( 10 - | |
| ( | ( ( 10 - ( | |
| 1 | ( ( 10 - ( 1 | |
| * | ( ( 10 - ( 1 * | |
| 2 | ( ( 10 - ( 1 * 2 | |
| ) | ( ( 10 - 2 | 1 * 2 = 2 & Push |
| ) | ( 8 | 10 - 2 = 8 & Push |
| / | ( 8 / | |
| ( | ( 8 / ( | |
| 9 | ( 8 / ( 9 | |
| - | ( 8 / ( 9 - | |
| 9 | ( 8 / ( 9 - 7 | |
| ) | ( 8 / 2 | 9 - 7 = 2 & Push |
| ) | 4 | 8 / 2 = 4 & Push |
| New line | Empty | Pop & Print |
C Program
int main (int argc, char
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2));
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (! cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d\n", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
Output of the program:
Input entered at the command line: (((2 * 5) - (1 * 2)) / (9 - 7)) [3]
Evaluation of Infix Expression which is not fully parenthesized[edit | edit source]
Input: (2 * 5 - 1 * 2) / (11 - 9)
Output: 4
Analysis: There are five types of input characters which are:
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
We do not know what to do if an operator is read as an input character. By implementing the priority rule for operators, we have a solution to this problem.
The Priority rule we should perform comparative priority check if an operator is read, and then push it. If the stack top contains an operator of prioirty higher than or equal to the priority of the input operator, then we pop it and print it. We keep on perforrming the prioirty check until the top of stack either contains an operator of lower priority or if it does not contain an operator.
Data Structure Requirement for this problem: A character stack and an integer stack
Algorithm:
1. Read an input character
2. Actions that will be performed at the end of each input
Opening brackets (2.1) Push it into stack and then Go to step (1)
Digit (2.2) Push into stack, Go to step (1)
Operator (2.3) Do the comparative priority check
(2.3.1) if the character stack's top contains an operator with equal
or higher priority, then pop it into op
Pop a number from integer stack into op2
Pop another number from integer stack into op1
Calculate op1 op op2 and push the result into the integer
stack
Closing brackets (2.4) Pop from the character stack
(2.4.1) if it is an opening bracket, then discard it and Go to
step (1)
(2.4.2) To op, assign the popped element
Pop a number from integer stack and assign it op2
Pop another number from integer stack and assign it
to op1
Calculate op1 op op2 and push the result into the integer
stack
Convert into character and push into stack
Go to the step (2.4)
New line character (2.5) Print the result after popping from the stack
STOP
Result: The evaluation of an infix expression that is not fully parenthesized is printed as follows:
Input String: (2 * 5 - 1 * 2) / (11 - 9)
| Input Symbol | Character Stack (from bottom to top) | Integer Stack (from bottom to top) | Operation performed |
|---|---|---|---|
| ( | ( | ||
| 2 | ( | 2 | |
| * | ( * | Push as * has higher priority | |
| 5 | ( * | 2 5 | |
| - | ( * | Since '-' has less priority, we do 2 * 5 = 10 | |
| ( - | 10 | We push 10 and then push '-' | |
| 1 | ( - | 10 1 | |
| * | ( - * | 10 1 | Push * as it has higher priority |
| 2 | ( - * | 10 1 2 | |
| ) | ( - | 10 2 | Perform 1 * 2 = 2 and push it |
| ( | 8 | Pop - and 10 - 2 = 8 and push, Pop ( | |
| / | / | 8 | |
| ( | / ( | 8 | |
| 11 | / ( | 8 11 | |
| - | / ( - | 8 11 | |
| 9 | / ( - | 8 11 9 | |
| ) | / | 8 2 | Perform 11 - 9 = 2 and push it |
| New line | 4 | Perform 8 / 2 = 4 and push it | |
| 4 | Print the output, which is 4 |
C Program
int main (int argc, char *argv[])
{
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*': while ((charactop->data != '(') && (!cemptystack(charactop)))
{
if(priority(rd) > (priority(charactop->data))
break;
else
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
}
charactop = cpush(charactop, rd);
break;
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2);
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (!= cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
Output of the program:
Input entered at the command line: (2 * 5 - 1 * 2) / (11 - 9)
Output: 4 [3]
Evaluation of Prefix Expression[edit | edit source]
Input: x + 6 * ( y + z ) ^ 3
Output:' 4
Analysis: There are three types of input characters
* Numbers
* Operators
* New line character (\n)
Data structure requirement: A character stack and an integer stack
Algorithm:
1. Read one character input at a time and keep pushing it into the character stack until the new
line character is reached
2. Perform pop from the character stack. If the stack is empty, go to step (3)
Number (2.1) Push in to the integer stack and then go to step (1)
Operator (2.2) Assign the operator to op
Pop a number from integer stack and assign it to op1
Pop another number from integer stack
and assign it to op2
Calculate op1 op op2 and push the output into the integer
stack. Go to step (2)
3. Pop the result from the integer stack and display the result
Result: The evaluation of prefix expression is printed as follows:
Input String: / - * 2 5 * 1 2 - 11 9
| Input Symbol | Character Stack (from bottom to top) | Integer Stack (from bottom to top) | Operation performed |
|---|---|---|---|
| / | / | ||
| - | / | ||
| * | / - * | ||
| 2 | / - * 2 | ||
| 5 | / - * 2 5 | ||
| * | / - * 2 5 * | ||
| 1 | / - * 2 5 * 1 | ||
| 2 | / - * 2 5 * 1 2 | ||
| - | / - * 2 5 * 1 2 - | ||
| 11 | / - * 2 5 * 1 2 - 11 | ||
| 9 | / - * 2 5 * 1 2 - 11 9 | ||
| \n | / - * 2 5 * 1 2 - 11 | 9 | |
| / - * 2 5 * 1 2 - | 9 11 | ||
| / - * 2 5 * 1 2 | 2 | 11 - 9 = 2 | |
| / - * 2 5 * 1 | 2 2 | ||
| / - * 2 5 * | 2 2 1 | ||
| / - * 2 5 | 2 2 | 1 * 2 = 2 | |
| / - * 2 | 2 2 5 | ||
| / - * | 2 2 5 2 | ||
| / - | 2 2 10 | 5 * 2 = 10 | |
| / | 2 8 | 10 - 2 = 8 | |
| Stack is empty | 4 | 8 / 2 = 4 | |
| Stack is empty | Print 4 |
C Program
int main (int argc, char *argv[])
{
struct ch *charactop = NULL;
struct integer *integertop = NULL;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
rd = argv[1][i];
while(rd != '\0')
{
charactop = cpush(charactop, rd);
rd = argv[1][i++];
}
while(!emptystack(charactop))
{
charactop = cpop(charactop, rd);
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
op = rd;
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
break;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
Output of the program:
Input entered at the command line: / - * 2 5 * 1 2 - 11 9
Output: 4 [3]
Conversion of an Infix expression that is fully parenthesized into a Postfix expression[edit | edit source]
Input: (((8 + 1) - (7 - 4)) / (11 - 9))
Output: 8 1 + 7 4 - - 11 9 - /
Analysis: There are five types of input characters which are:
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
Requirement: A character stack
Algorithm:
1. Read an character input
2. Actions to be performed at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Print and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from the stack
(2.4.1) If it is an operator, print it, Go to step (1)
(2.4.2) If the popped element is an opening bracket,
discard it and go to step (1)
New line character (2.5) STOP
Therefore, the final output after conversion of an infix expression to a postfix expression is as follows:
| Input | Operation | Stack (after op) | Output on monitor |
|---|---|---|---|
| ( | (2.1) Push operand into stack | ( | |
| ( | (2.1) Push operand into stack | ( ( | |
| ( | (2.1) Push operand into stack | ( ( ( | |
| 8 | (2.2) Print it | 8 | |
| + | (2.3) Push operator into stack | ( ( ( + | 8 |
| 1 | (2.2) Print it | 8 1 | |
| ) | (2.4) Pop from the stack: Since popped element is '+' print it | ( ( ( | 8 1 + |
| (2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character | ( ( | 8 1 + | |
| - | (2.3) Push operator into stack | ( ( - | |
| ( | (2.1) Push operand into stack | ( ( - ( | |
| 7 | (2.2) Print it | 8 1 + 7 | |
| - | (2.3) Push the operator in the stack | ( ( - ( - | |
| 4 | (2.2) Print it | 8 1 + 7 4 | |
| ) | (2.4) Pop from the stack: Since popped element is '-' print it | ( ( - ( | 8 1 + 7 4 - |
| (2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character | ( ( - | ||
| ) | (2.4) Pop from the stack: Since popped element is '-' print it | ( ( | 8 1 + 7 4 - - |
| (2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character | ( | ||
| / | (2.3) Push the operand into the stack | ( / | |
| ( | (2.1) Push into the stack | ( / ( | |
| 11 | (2.2) Print it | 8 1 + 7 4 - - 11 | |
| - | (2.3) Push the operand into the stack | ( / ( - | |
| 9 | (2.2) Print it | 8 1 + 7 4 - - 11 9 | |
| ) | (2.4) Pop from the stack: Since popped element is '-' print it | ( / ( | 8 1 + 7 4 - - 11 9 - |
| (2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character | ( / | ||
| ) | (2.4) Pop from the stack: Since popped element is '/' print it | ( | 8 1 + 7 4 - - 11 9 - / |
| (2.4) Pop from the stack: Since popped element is '(' we ignore it and read next character | Stack is empty | ||
| New line character | (2.5) STOP |
Rearranging railroad cars[edit | edit source]
Problem Description[edit | edit source]
It's a very nice application of stacks. Consider that a freight train has n railroad cars, each to be left at a different station. They're numbered 1 through n and a freight train visits these stations in order n through 1. Obviously, the railroad cars are labeled by their destination.To facilitate removal of the cars from the train, we must rearrange them in ascending order of their number (i.e., 1 through n). When cars are in this order, they can be detached at each station. We rearrange cars at a shunting yard that has input track, output track & k holding tracks between the input & output tracks (i.e., holding track).
Solution Strategy[edit | edit source]
To rearrange cars, we examine the cars on the input from front to back. If the car being examined is the next one in the output arrangement, we move it directly to output track. If not, we move it to the holding track and leave it there until it's time to place it to the output track. The holding tracks operate in a LIFO manner as the cars enter and leave these tracks from the top. When rearranging cars, only the following moves are permitted:
- A car may be moved from the front (i.e., right end) of the input track to the top of one of the holding tracks or to the left end of the output track.
- A car may be moved from the top of the holding track to the left end of the output track.
The figure shows a shunting yard with k = 3, holding tracks H1, H2 and H3, and n = 9. The n cars of the freight train begin in the input track and are to end up in the output track in order 1 through n from right to left. The cars initially are in the order 5, 8, 1, 7, 4, 2, 9, 6, 3 from back to front. Later cars are rearranged in the desired order.
A Three-Track Example[edit | edit source]

- Consider the input arrangement from the figure, here we note that car 3 is at the front, so it can't be output yet, as it is to be preceded by cars 1 and 2. So car 3 is detached and moved to holding track H1.
- The next car 6 can't be output and it is moved to holding track H2. Because we have to output car 3 before car 6 and this will not be possible if we move car 6 to holding track H1.
- Now it's obvious that we move car 9 to H3.
The requirement of rearrangement of cars on any holding track is that the cars should be preferred to arrange in ascending order from top to bottom.
- So car 2 is now moved to holding track H1 so that it satisfies the previous statement. If we move car 2 to H2 or H3, then we've no place to move cars 4, 5, 7, or 8.The least restrictions on future car placement arise when the new car λ is moved to the holding track that has a car at its top with smallest label Ψ such that λ < Ψ. We may call it an assignment rule to decide whether a particular car belongs to a specific holding track.
- When car 4 is considered, there are three places to move the car: H1, H2, and H3. The top of these tracks are 2, 6, and 9.So using the aforementioned Assignment rule, we move car 4 to H2.
- Car 7 is moved to H3.
- The next car 1 has the lowest label, so it's moved to the output track.
- Now it's time for cars 2 and 3 to output which are from H1 (in short, all the cars from H1 are appended to car 1 on the output track).
Car 4 is moved to the output track. No other cars can be moved to the output track at this time.
- The next car, car 8, is moved to holding track H1.
- Car 5 is output from the input track. Car 6 is moved to the output track from H2, so is car 7 from H3, car 8 from H1, and car 9 from H3.
Quicksort[edit | edit source]
Sorting means arranging a group of elements in a particular order. Be it ascending or descending, by cardinality or alphabetical order or variations thereof. The resulting ordering possibilities will only be limited by the type of the source elements.
Quicksort is an algorithm of the divide and conquer type. In this method, to sort a set of numbers, we reduce it to two smaller sets, and then sort these smaller sets.
This can be explained with the help of the following example:
Suppose A is a list of the following numbers:
In the reduction step, we find the final position of one of the numbers. In this case, let us assume that we have to find the final position of 48, which is the first number in the list.
To accomplish this, we adopt the following method. Begin with the last number, and move from right to left. Compare each number with 48. If the number is smaller than 48, we stop at that number and swap it with 48.
In our case, the number is 24. Hence, we swap 24 and 48.
The numbers 96 and 72 to the right of 48, are greater than 48. Now beginning with 24, scan the numbers in the opposite direction, that is from left to right. Compare every number with 48 until you find a number that is greater than 48.
In this case, it is 60. Therefore we swap 48 and 60.
Note that the numbers 12, 24 and 36 to the left of 48 are all smaller than 48. Now, start scanning numbers from 60, in the right to left direction. As soon as you find lesser number, swap it with 48.
In this case, it is 44. Swap it with 48. The final result is:
Now, beginning with 44, scan the list from left to right, until you find a number greater than 48.
Such a number is 84. Swap it with 48. The final result is:
Now, beginning with 84, traverse the list from right to left, until you reach a number lesser than 48. We do not find such a number before reaching 48. This means that all the numbers in the list have been scanned and compared with 48. Also, we notice that all numbers less than 48 are to the left of it, and all numbers greater than 48, are to its right.
The final partitions look as follows:
Therefore, 48 has been placed in its proper position and now our task is reduced to sorting the two partitions. This above step of creating partitions can be repeated with every partition containing 2 or more elements. As we can process only a single partition at a time, we should be able to keep track of the other partitions, for future processing.
This is done by using two stacks called LOWERBOUND and UPPERBOUND, to temporarily store these partitions. The addresses of the first and last elements of the partitions are pushed into the LOWERBOUND and UPPERBOUND stacks respectively. Now, the above reduction step is applied to the partitions only after its boundary values are popped from the stack.
We can understand this from the following example:
Take the above list A with 12 elements. The algorithm starts by pushing the boundary values of A, that is 1 and 12 into the LOWERBOUND and UPPERBOUND stacks respectively. Therefore the stacks look as follows:
LOWERBOUND: 1 UPPERBOUND: 12
To perform the reduction step, the values of the stack top are popped from the stack. Therefore, both the stacks become empty.
LOWERBOUND: {empty} UPPERBOUND: {empty}
Now, the reduction step causes 48 to be fixed to the 5th position and creates two partitions, one from position 1 to 4 and the other from position 6 to 12. Hence, the values 1 and 6 are pushed into the LOWERBOUND stack and 4 and 12 are pushed into the UPPERBOUND stack.
LOWERBOUND: 1, 6 UPPERBOUND: 4, 12
For applying the reduction step again, the values at the stack top are popped. Therefore, the values 6 and 12 are popped. Therefore the stacks look like:
LOWERBOUND: 1 UPPERBOUND: 4
The reduction step is now applied to the second partition, that is from the 6th to 12th element.
After the reduction step, 98 is fixed in the 11th position. So, the second partition has only one element. Therefore, we push the upper and lower boundary values of the first partition onto the stack. So, the stacks are as follows:
LOWERBOUND: 1, 6 UPPERBOUND: 4, 10
The processing proceeds in the following way and ends when the stacks do not contain any upper and lower bounds of the partition to be processed, and the list gets sorted.
The Stock Span Problem[edit | edit source]
In the stock span problem, we will solve a financial problem with the help of stacks.
Suppose, for a stock, we have a series of n daily price quotes, the span of the stock's price on a particular day is defined as the maximum number of consecutive days for which the price of the stock on the current day is less than or equal to its price on that day.
An algorithm which has Quadratic Time Complexity[edit | edit source]
Input: An array P with n elements
Output: An array S of n elements such that S[i] is the largest integer k such that k <= i + 1 and P[j] <= P[i] for j = i - k + 1,.....,i
Algorithm:
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 repeat
3.3.1 if (P[i - k] <= P[i]) then
Increment k by 1
3.3.2 else
Done with true condition
3.4 Till (k > i) or done with processing
Assign value of k to S[i] to get the span of the stock
4. Return array S
Now, analyzing this algorithm for running time, we observe:
- We have initialized the array S at the beginning and returned it at the end. This is a constant time operation, hence takes O(n) time
- The repeat loop is nested within the for loop. The for loop, whose counter is i is executed n times. The statements which are not in the repeat loop, but in the for loop are executed n times. Therefore these statements and the incrementing and condition testing of i take O(n) time.
- In repetition of i for the outer for loop, the body of the inner repeat loop is executed maximum i + 1 times. In the worst case, element S[i] is greater than all the previous elements. So, testing for the if condition, the statement after that, as well as testing the until condition, will be performed i + 1 times during iteration i for the outer for loop. Hence, the total time taken by the inner loop is O(n(n + 1)/2), which is O()
The running time of all these steps is calculated by adding the time taken by all these three steps. The first two terms are O() while the last term is O(). Therefore the total running time of the algorithm is O().
An algorithm that has Linear Time Complexity[edit | edit source]
In order to calculate the span more efficiently, we see that the span on a particular day can be easily calculated if we know the closest day before i, such that the price of the stocks on that day was higher than the price of the stocks on the present day. If there exists such a day, we can represent it by h(i) and initialize h(i) to be -1.
Therefore the span of a particular day is given by the formula, s = i - h(i).
To implement this logic, we use a stack as an abstract data type to store the days i, h(i), h(h(i)) and so on. When we go from day i-1 to i, we pop the days when the price of the stock was less than or equal to p(i) and then push the value of day i back into the stack.
Here, we assume that the stack is implemented by operations that take O(1) that is constant time. The algorithm is as follows:
Input: An array P with n elements and an empty stack N
Output: An array S of n elements such that P[i] is the largest integer k such that k <= i + 1 and P[y] <= P[i] for j = i - k + 1,.....,i
Algorithm:
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 while not (Stack N is empty or done with processing)
3.3.1 if ( P[i] >= P[N.top())] then
Pop a value from stack N
3.3.2 else
Done with true condition
3.4 if Stack N is empty
3.4.1 Initialize h to -1
3.5 else
3.5.1 Initialize stack top to h
3.5.2 Put the value of h - i in S[i]
3.5.3 Push the value of i in N
4. Return array S
Now, analyzing this algorithm for running time, we observe:
- We have initialized the array S at the beginning and returned it at the end. This is a constant time operation, hence takes O(n) time
- The while loop is nested within the for loop. The for loop, whose counter is i is executed n times. The statements which are not in the repeat loop, but in the for loop are executed n times. Therefore these statements and the incrementing and condition testing of i take O(n) time.
- Now, observe the inner while loop during i repetitions of the for loop. The statement done with a true condition is done at most once, since it causes an exit from the loop. Let us say that t(i) is the number of times statement Pop a value from stack N is executed. So it becomes clear that while not (Stack N is empty or done with processing) is tested maximum t(i) + 1 times.
- Adding the running time of all the operations in the while loop, we get:
- An element once popped from the stack N is never pushed back into it. Therefore,
So, the running time of all the statements in the while loop is O()
The running time of all the steps in the algorithm is calculated by adding the time taken by all these steps. The run time of each step is O(). Hence the running time complexity of this algorithm is O().
Related Links[edit | edit source]
Queues[edit | edit source]
A queue is a basic data structure that is used throughout programming. You can think of it as a line in a grocery store. The first one in the line is the first one to be served.Just like a queue.
A queue is also called a FIFO (First In First Out) to demonstrate the way it accesses data.
Queue<item-type> Operations
enqueue(new-item:item-type)- Adds an item onto the end of the queue.
front():item-type- Returns the item at the front of the queue.
dequeue()- Removes the item from the front of the queue.
is-empty():Boolean- True if no more items can be dequeued and there is no front item.
is-full():Boolean- True if no more items can be enqueued.
get-size():Integer- Returns the number of elements in the queue.
All operations except get-size() can be performed in time. get-size() runs in at worst
Linked List Implementation[edit | edit source]
The basic linked list implementation uses a singly-linked list with a tail pointer to keep track of the back of the queue.
type Queue<item_type>
data list:Singly Linked List<item_type>
data tail:List Iterator<item_type>
constructor()
list := new Singly-Linked-List()
tail := list.get-begin() # null
end constructor
When you want to enqueue something, you simply add it to the back of the item pointed to by the tail pointer. So the previous tail is considered next compared to the item being added and the tail pointer points to the new item. If the list was empty, this doesn't work, since the tail iterator doesn't refer to anything
method enqueue(new_item:item_type)
if is-empty()
list.prepend(new_item)
tail := list.get-begin()
else
list.insert_after(new_item, tail)
tail.move-next()
end if
end method
The front item on the queue is just the one referred to by the linked list's head pointer
method front():item_type
return list.get-begin().get-value()
end method
When you want to dequeue something off the list, simply point the head pointer to the previous from head item. The old head item is the one you removed of the list. If the list is now empty, we have to fix the tail iterator.
method dequeue()
list.remove-first()
if is-empty()
tail := list.get-begin()
end if
end method
A check for emptiness is easy. Just check if the list is empty.
method is-empty():Boolean
return list.is-empty()
end method
A check for full is simple. Linked lists are considered to be limitless in size.
method is-full():Boolean
return False
end method
A check for the size is again passed through to the list.
method get-size():Integer
return list.get-size()
end method
end type
Performance Analysis[edit | edit source]
In a linked list, accessing the first element is an operation because the list contains a pointer directly to it. Therefore, enqueue, front, and dequeue are a quick operations.
The checks for empty/fullness as done here are also .
The performance of getSize() depends on the performance of the corresponding operation in the linked list implementation. It could be either , or , depending on what time/space tradeoff is made. Most of the time, users of a Queue do not use the getSize() operation, and so a bit of space can be saved by not optimizing it.
Circular Array Implementation[edit | edit source]
Performance Analysis[edit | edit source]
Priority Queue Implementation[edit | edit source]
Related Links[edit | edit source]
Deques[edit | edit source]
A Deque is a homogeneous list of elements in which insertions and deletion operations are performed on both the ends.
Because of this property it is known as double ended queue i.e. Deque
Deque has two types:
- Input restricted queue: It allows insertion at only one end
- Output restricted queue: It allows deletion at only one end
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
References[edit | edit source]
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Trees[edit | edit source]
A tree is a non-empty set with an element that is designated as the root of the tree while the remaining elements are partitioned into non-empty sets each of which is a subtree of the root.
Tree nodes have many useful properties. The depth of a node is the length of the path (or the number of edges) from the root to that node. The height of a node is the longest path from that node to its leaves. The height of a tree is the height of the root. A leaf node has no children—its only path is up to its parent.
See the axiomatic development of trees and its consequences for more information.
Types of trees:
Binary: Each node has zero, one, or two children. This assertion makes many tree operations simple and efficient.
Binary Search: A binary tree where any left child node has a value less than its parent node and any right child node has a value greater than or equal to that of its parent node.
Traversal[edit | edit source]
Many problems require we visit the nodes of a tree in a systematic way: tasks such as counting how many nodes exist or finding the maximum element. Three different methods are possible for binary trees: preorder, postorder, and in-order, which all do the same three things: recursively traverse both the left and right subtrees and visit the current node. The difference is when the algorithm visits the current node:
preorder: Current node, left subtree, right subtree (DLR)
postorder: Left subtree, right subtree, current node (LRD)
in-order: Left subtree, current node, right subtree (LDR)
levelorder: Level by level, from left to right, starting from the root node.
- Visit means performing some operation involving the current node of a tree, like incrementing a counter or checking if the value of the current node is greater than any other recorded.
Sample implementations for Tree Traversal[edit | edit source]
preorder(node) visit(node) if node.left ≠ null then preorder(node.left) if node.right ≠ null then preorder(node.right)
inorder(node) if node.left ≠ null then inorder(node.left) visit(node) if node.right ≠ null then inorder(node.right)
postorder(node) if node.left ≠ null then postorder(node.left) if node.right ≠ null then postorder(node.right) visit(node)
levelorder(root) queue<node> q q.push(root) while not q.empty do node = q.pop visit(node) if node.left ≠ null then q.push(node.left) if node.right ≠ null then q.push(node.right)
For an algorithm that is less taxing on the stack, see Threaded Trees.
Examples of Tree Traversals[edit | edit source]
preorder: 50,30, 20, 40, 90, 100 inorder: 20,30,40,50, 90, 100 postorder: 20,40,30,100,90,50
Balancing[edit | edit source]
When entries that are already sorted are stored in a tree, all new records will go the same route, and the tree will look more like a list (such a tree is called a degenerate tree). Therefore the tree needs balancing routines, making sure that under all branches are an equal number of records. This will keep searching in the tree at optimal speed. Specifically, if a tree with n nodes is a degenerate tree, the longest path through the tree will be n nodes; if it is a balanced tree, the longest path will be log n nodes.
Algorithms/Left rotation: This shows how balancing is applied to establish a priority heap invariant in a Treap, a data structure which has the queueing performance of a heap, and the key lookup performance of a tree. A balancing operation can change the tree structure while maintaining another order, which is binary tree sort order. The binary tree order is left to right, with left nodes' keys less than right nodes' keys, whereas the priority order is up and down, with higher nodes' priorities greater than lower nodes' priorities. Alternatively, the priority can be viewed as another ordering key, except that finding a specific key is more involved.
The balancing operation can move nodes up and down a tree without affecting the left right ordering.
AVL: A balanced binary search tree according to the following specification: the heights of the two child subtrees of any node differ by at most one.
Red-Black Tree: A balanced binary search tree using a balancing algorithm based on colors assigned to a node, and the colors of nearby nodes.
AA Tree: A balanced tree, in fact a more restrictive variation of a red-black tree.
Binary Search Trees[edit | edit source]
A typical binary search tree looks like this:
Terms[edit | edit source]
Node Any item that is stored in the tree. Root The top item in the tree. (50 in the tree above) Child Node(s) under the current node. (20 and 40 are children of 30 in the tree above) Parent The node directly above the current node. (90 is the parent of 100 in the tree above) Leaf A node which has no children. (20 is a leaf in the tree above)
Searching through a binary search tree[edit | edit source]
To search for an item in a binary tree:
- Start at the root node
- If the item that you are searching for is less than the root node, move to the left child of the root node, if the item that you are searching for is more than the root node, move to the right child of the root node and if it is equal to the root node, then you have found the item that you are looking for.
- Now check to see if the item that you are searching for is equal to, less than or more than the new node that you are on. Again if the item that you are searching for is less than the current node, move to the left child, and if the item that you are searching for is greater than the current node, move to the right child.
- Repeat this process until you find the item that you are looking for or until the node does not have a child on the correct branch, in which case the tree doesn't contain the item which you are looking for.
Example[edit | edit source]
For example, to find the node 40...
- The root node is 50, which is greater than 40, so you go to 50's left child.
- 50's left child is 30, which is less than 40, so you next go to 30's right child.
- 30's right child is 40, so you have found the item that you are looking for :)
.........
Adding an item to a binary search tree[edit | edit source]
- To add an item, you first must search through the tree to find the position that you should put it in. You do this following the steps above.
- When you reach a node which doesn't contain a child on the correct branch, add the new node there.
For example, to add the node 25...
- The root node is 50, which is greater than 25, so you go to 50's left child.
- 50's left child is 30, which is greater than 25, so you go to 30's left child.
- 30's left child is 20, which is less than 25, so you go to 20's right child.
- 20's right child doesn't exist, so you add 25 there :)
Deleting an item from a binary search tree[edit | edit source]
It is assumed that you have already found the node that you want to delete, using the search technique described above.
Case 1: The node you want to delete is a leaf[edit | edit source]
For example, to delete 40...
- Simply delete the node!
Case 2: The node you want to delete has one child[edit | edit source]
- Directly connect the child of the node that you want to delete, to the parent of the node that you want to delete.
For example, to delete 90...
- Delete 90, then make 100 the child node of 50.
Case 3: The node you want to delete has two children[edit | edit source]
One non-standard way, is to rotate the node into a chosen subtree, and attempt to delete the key again from that subtree, recursively, until Case 1 or Case 2 occurs. This could unbalance a tree, so randomly choosing whether to right or left rotate may help.
The standard way is to pick either the left or right child, say the right, then get the right's leftmost descendent by following left ,starting from the right child, until the next left is null. Then remove this leftmost descendant of the right child, replacing it with its right sub-tree ( it has a left child of null). Then use the contents of this former leftmost descendant of the right child, as replacement for the key and value of the node being deleted , so that its values now are in the deleted node, the parent of the right child. This still maintains the key ordering for all nodes. Example java code is below in the treap example code.
The following examples use the standard algorithm, that is, the successor is the left-most node in the right subtree of the node to be deleted.
For example, to delete 30
- The right node of the node which is being deleted is 40.
- (From now on, we continually go to the left node until there isn't another one...) The first left node of 40, is 35.
- 35 has no left node, therefore 35 is the successor!
- 35 replaces 30, at the original right node, and the node with 35 is deleted, replacing it with the right sub-tree, which has the root node 37.
Case 1 of two-children case: The successor is the right child of the node being deleted[edit | edit source]
- Directly move the child to the right of the node being deleted into the position of the node being deleted.
- As the new node has no left children, you can connect the deleted node's left subtree's root as it's left child.
For example, to delete 30
- replace the contents to be deleted (30), with the successor's contents( 40).
- delete the successor node (contents 40), replacing it with its right subtree (head contents 45).
Case 2 of two-children case: The successor isn't the right child of the node being deleted[edit | edit source]
This is best shown with an example
To delete 30...
- Replace the contents to be deleted (30) with the successor's contents (35).
- replace the successor (35) with it's right subtree (37). There is no left subtree because the successor is leftmost.
Example extract of Java code for binary tree delete operation[edit | edit source]
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del);
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// non-standard method,
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
Red-Black trees[edit | edit source]
A red-black tree is a self-balancing tree structure that applies a color to each of its nodes. The structure of a red-black tree must adhere to a set of rules which dictate how nodes of a certain color can be arranged. The application of these rules is performed when the tree is modified in some way, causing the rotation and recolouring of certain nodes when a new node is inserted or an old node is deleted. This keeps the red-black tree balanced, guaranteeing a search complexity of O(log n).
The rules that a red-black tree must adhere to are as follows:
- Each node must be either red or black.
- The root is always black.
- All leaves within the tree are black (leaves do not contain data and can be modelled as null or nil references in most programming languages).
- Every red node must have two black child nodes.
- Every path from a given node to any of its descendant leaves must contain the same number of black nodes.
A red-black tree can be modelled as 2-3-4 tree , which is a sub-class of B tree (below). A black node with one red node can be seen as linked together as a 3-node , and a black node with 2 red child nodes can be seen as a 4-node.
4-nodes are split , producing a two node, and the middle node made red, which turns a parent of the middle node which has no red child from a 2-node to a 3-node, and turns a parent with one red child into a 4-node (but this doesn't occur with always left red nodes).
A in-line arrangement of two red nodes, is rotated into a parent with two red children, a 4-node, which is later split, as described before.
A right rotate 'split 4-node' |red
red / \ --> B ---> B
B red/ \red / \
red / \ C A C A
C D / /
D D
An optimization mentioned by Sedgewick is that all right inserted red nodes are left rotated to become left red nodes, so that only inline left red nodes ever have to be rotated right before splitting. AA-trees (above) by Arne Anderson , described in a paper in 1993 , seem an earlier exposition of the simplification, however he suggested right-leaning 'red marking' instead of left leaning , as suggested by Sedgewick, but AA trees seem to have precedence over left leaning red black trees. It would be quite a shock if the Linux CFS scheduler was described in the future as 'AA based'.
In summary, red-black trees are a way of detecting two insertions into the same side, and levelling out the tree before things get worse . Two left sided insertions will be rotated, and the two right sided insertions, would look like two left sided insertions after left rotation to remove right leaning red nodes. Two balanced insertions for the same parent could result in a 4-node split without rotation, so the question arises as to whether a red black tree could be attacked with serial insertions of one sided triads of a < P < b , and then the next triad's P' < a.
Python illustrative code follows
RED = 1
BLACK = 0
class Node:
def __init__(self, k, v):
# all newly inserted node's are RED
self.color = RED
self.k = k
self.v = v
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.root = None
def insert(self, k, v) :
self.root = self._insert(self.root, k,v)
def _insert(self, n , k, v):
if n is None:
return Node(k,v)
if k < n.k :
n.left = self._insert(n.left, k , v)
elif k > n.k :
n.right = self._insert(n.right, k, v)
if n.right.color is RED:
#always on the left red's
#left rotate
tmp = n.right
n.right = tmp.left
tmp.left = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.left.color
n.left.color = tmpcolor
if n.left <> None and n.left.left <> None and n.left.left.color == RED and n.left.color == RED:
# right rotate in-line reds
print "right rotate"
tmp = n.left
n.left = tmp.right
tmp.right = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.right.color
n.right.color = tmpcolor
if n.left <> None: print n.left.color, n.color, n.right.color
#no need to test, because after right rotation, will need to split 3-node , as right rotation has
#brought red left grandchild to become left red child, and left red child is now red right child
#so there are two red children.
#if n.left <> None and n.right <> None and n.left.color == RED and n.right.color == RED:
print "split"
n.color = RED
n.left.color = BLACK
n.right.color = BLACK
return n
def find(self, k):
return self._find_rb(k, self.root)
def _find_rb(self, k, n):
if n is None:
return None
if k < n.k:
return self._find_rb( k, n.left)
if k > n. k:
return self._find_rb( k, n.right)
return n.v
def inorder(self):
self.inorder_visit(self.root, "O")
def inorder_visit(self, node,label=""):
if node is None: return
self.inorder_visit(node.left, label+"/L")
print label, "val=", node.v
self.inorder_visit(node.right, label+"/R")
def test1(N):
t = RBTree()
for i in xrange(0,N):
t.insert(i,i)
l = []
t.inorder()
for i in xrange(0,N):
x =t.find(i)
if x <> None:
l.append((x, i) )
print "found", len(l)
if __name__ == "__main__":
import random
test1(100000)
test1(1000)
test1(100)
test1(10)
B Trees[edit | edit source]
Summary[edit | edit source]
- Whereas binary trees have nodes that have two children, with the left child and all of its descendants less than the "value" of the node, and the right child and all of its children more than the "value" of the node, a B-tree is a generalization of this.
- The generalization is that instead of one value, the node has a list of values, and the list is of size n ( n > 2 ). n is chosen to optimize storage , so that a node corresponds in size to a block for instance. This is in the days before ssd drives, but searching binary nodes stored on ssd ram would still be slower than searching ssd ram for a block of values, loading into normal ram and cpu cache, and searching the loaded list.
- At the start of the list, the left child of the first element of the list has a value less than the first element , and so do all its children. To the right of the first element, is a child which has values more than the first element's value, as do all of its children, but also less than the value of the second element. Induction can be used , and this holds so for the child between element 1 and 2, 2 and 3, ... so on until n-1 and nth node.
- To insert into a non-full B tree node, is to do a insertion into a sorted list.
- In a B+ tree, insertions can only be done in leaf nodes, and non-leaf nodes hold copies of a demarcating value between adjacent child nodes e.g. the left most value of an element's right child's list of nodes.
- Whenever a list becomes full e.g. there are n nodes, the node is "split", and this means making two new nodes, and passing the demarcating value upto the parent.
B Trees were described originally as generalizations of binary search trees , where a binary tree is a 2-node B-Tree, the 2 standing for two children, with 2-1 = 1 key separating the 2 children. Hence a 3-node has 2 values separating 3 children, and a N node has N children separated by N-1 keys.
A classical B-Tree can have N-node internal nodes, and empty 2-nodes as leaf nodes, or more conveniently, the children can either be a value or a pointer to the next N-node, so it is a union.
The main idea with B-trees is that one starts with a root N-node , which is able to hold N-1 entries, but on the Nth entry, the number of keys for the node is exhausted, and the node can be split into two half sized N/2 sized N nodes, separated by a single key K, which is equal to the right node's leftmost key, so any entry with key K2 equal or greater than K goes in the right node, and anything less than K goes in the left. When the root node is split, a new root node is created with one key, and a left child and a right child. Since there are N children but only N-1 entries, the leftmost child is stored as a separate pointer. If the leftmost pointer splits, then the left half becomes the new leftmost pointer, and the right half and separating key is inserted into the front of the entries.
An alternative is the B+ tree which is the most commonly used in database systems, because only values are stored in leaf nodes, whereas internal nodes only store keys and pointers to other nodes, putting a limit on the size of the datum value as the size of a pointer. This often allows internal nodes with more entries able to fit a certain block size, e.g. 4K is a common physical disc block size. Hence , if a B+ tree internal node is aligned to a physical disc block, then the main rate limiting factor of reading a block of a large index from disc because it isn't cached in a memory list of blocks is reduced to one block read.
A B+ tree has bigger internal nodes, so is wider and shorter in theory than an equivalent B tree which must fit all nodes within a given physical block size, hence overall it is a faster index due to greater fan out and less height to reach keys on average.
Apparently, this fan out is so important, compression can also be applied to the blocks to increase the number of entries fitting within a given underlying layer's block size (the underlying layer is often a filesystem block).
Most database systems use the B+ tree algorithm, including postgresql, mysql, derbydb, firebird, many Xbase index types, etc.
Many filesystems also use a B+ tree to manage their block layout (e.g. xfs, NTFS, etc).
Transwiki has a java implementation of a B+ Tree which uses traditional arrays as key list and value list.
Below is an example of a B Tree with test driver, and a B+ tree with a test driver. The memory / disc management is not included, but a usable hacked example can be found at Hashing Memory Checking Example.
This B+ tree implementation was written out of the B Tree , and the difference from the transwiki B+ tree is that it tries to use the semantics of SortedMap and SortedSet already present in the standard Java collections library.
Hence , the flat leaf block list of this B+ implementation can't contain blocks that don't contain any data, because the ordering depends on the first key of the entries, so a leaf block needs to be created with its first entry.
A B tree java example[edit | edit source]
package btreemap;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.TreeMap;
/** can't work without setting a comparator */
public class BTreeMap<K, V> implements SortedMap<K, V> {
private static final int NODE_SIZE = 100;
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return comparator;
}
Comparator< ? super K> defaultComparator = new
Comparator< K>() {
@Override
public int compare(K o1, K o2) {
// TODO Auto-generated method stub
Comparable c1 = (Comparable)o1;
Comparable c2 = (Comparable)o2;
return c1.compareTo(c2);
}
};
Comparator<? super K> comparator = defaultComparator;
BTBlock<K, V> root = new BTBlock<K, V>(NODE_SIZE, comparator);
/**
*
* @param comparator
* - this is mandatory for the tree to work
*/
public void setComparator(Comparator<? super K> comparator) {
this.comparator = comparator;
root = new BTBlock<K, V>(NODE_SIZE, comparator);
}
/**
*
*
*
* @param <K>
* @param <V>
* the entry is associated with a right child block.
*
*/
static class BlockEntry<K, V> {
K k;
V v;
BTBlock left;
BlockEntry() {
}
BlockEntry(K k, V v) {
left = null;
this.k = k;
this.v = v;
}
}
/**
*
* - this represents the result of splitting a full block into
* a left block, and a right block, and a median key, the right
* block and the median key held in a BlockEntry structure as above.
* @param <K>
* @param <V>
* @param <V>g
*/
static class SplitRootEntry<K, V> {
BTBlock<K, V> right;
BlockEntry<K, V> entry;
SplitRootEntry(BlockEntry<K, V> entry, BTBlock<K, V> right) {
this.right = right;
this.entry = entry;
}
SplitRootEntry() {
super();
}
}
/**
* this is used to return a result of a possible split , during recursive
* calling.
*
*
*
* @param <K>
* @param <V>
*/
static class resultAndSplit<K, V> {
/**
* null , if there is no split.
*/
SplitRootEntry<K, V> splitNode;
V v;
resultAndSplit(V v) {
this.v = v;
}
resultAndSplit(SplitRootEntry<K, V> entry, V v) {
this.v = v;
this.splitNode = entry;
}
}
/**
* used to represent the insertion point after searching a block if compare
* is zero, then a match was found, and pos is the insertion entry if
* compare < 0 and pos == 0 , then the search ended up less than the
* leftmost entry else compare > 0 , and the search will be to the immediate
* right of pos.
*
*
*
*/
static class PosAndCompare {
int pos = 0;
int compare = 0;
}
static class BTBlock<K, V> {
List<BlockEntry<K, V>> entries;
BTBlock<K, V> rightBlock = null;
private int maxSz = 0;
Comparator<? super K> comparator;
Comparator<? super K> comparator() {
return comparator;
}
public BTBlock(int size, Comparator<? super K> c) {
entries = new ArrayList<BlockEntry<K, V>>();
maxSz = size;
this.comparator = c;
}
/**
* PosAndCompare usage: if compare is zero, then a match was found, and
* pos is the insertion entry if compare < 0 and pos == 0 , then the
* search ended up less than the leftmost entry else compare > 0 , and
* the search will be to the immediate right of pos.
*
*
*
*/
// private void blockSearch(K k, PosAndCompare pc) {
// for (int i = 0; i < entries.size(); ++i) {
// pc.compare = comparator.compare(k, entries.get(i).k);
// if (pc.compare == 0) {
// pc.pos = i;
// return;
// }
// if (pc.compare < 0 && i == 0) {
// pc.pos = 0;
// return;
// }
//
// if (pc.compare < 0) {
// pc.pos = i - 1;
// pc.compare = 1;
// return;
// }
//
// }
// pc.pos = entries.size() - 1;
// pc.compare = 1;
//
// // binary search, it's hard to get it right !
// // int left = 0;
// // int right = entries.size();
// //
// // while (left <= right && left < entries.size()) {
// // // pc.pos = (right - left) / 2 + left;
// // pc.pos = (left + right) / 2;
// // pc.compare = comparator().compare(k, entries.get(pc.pos).k);
// // if (pc.compare < 0) {
// // right = pc.pos - 1;
// // } else if (pc.compare > 0) {
// // left = pc.pos + 1;
// // } else {
// // return;
// // }
// // }
// //
// // BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
// // pc.pos = Collections.binarySearch(entries, e, cmp);
//
// }
Comparator<BlockEntry<K, V>> cmp = new Comparator<BlockEntry<K, V>>() {
@Override
public int compare(BlockEntry<K, V> o1, BlockEntry<K, V> o2) {
// TODO Auto-generated method stub
return comparator.compare(o1.k, o2.k);
}
};
resultAndSplit<K, V> put(K k, V v) {
V v2;
if (entries.size() == 0) {
entries.add(new BlockEntry<K, V>(k, v));
return new resultAndSplit<K, V>(v);
} else {
// PosAndCompare pc = new PosAndCompare();
BlockEntry<K, V> e = new BlockEntry<K, V>(k, v);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
// blockSearch(k, pc);
// a match
if (res >= 0) {
v2 = entries.get(res).v;
entries.get(res).v = v;
return new resultAndSplit<K, V>(v2);
}
// follow leftBlock if search is to left of first entry
if (index == entries.size() && rightBlock != null) {
resultAndSplit<K, V> result = rightBlock.put(k, v);
if (result.splitNode != null) {
rightBlock = result.splitNode.right;
entries.add(result.splitNode.entry);
}
} else if (index == entries.size() && rightBlock == null
&& entries.size() == maxSz) {
rightBlock = new BTBlock<K, V>(this.maxSz, comparator);
resultAndSplit<K, V> result = rightBlock.put(k, v);
} else if (index < entries.size()
&& entries.get(index).left != null) {
// follow right block if it exists
resultAndSplit<K, V> result = entries.get(index).left.put(
k, v);
if (result.splitNode != null) {
entries.get(index).left = result.splitNode.right;
// add to the left
entries.add(index, result.splitNode.entry);
}
} else {
// add to the left
entries.add(index, e);
}
// check if overflowed block , split if it has.
if (entries.size() > maxSz) {
int mid = entries.size() / 2;
// copy right half to new entries list.
List<BlockEntry<K, V>> leftEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = 0; i < mid; ++i) {
leftEntries.add(entries.get(i));
}
BlockEntry<K, V> centreEntry = entries.get(mid);
BTBlock<K, V> leftBlock = new BTBlock<K, V>(maxSz,
comparator);
leftBlock.entries = leftEntries;
// the median entry's left block is the new left block's
// leftmost block
leftBlock.rightBlock = centreEntry.left;
// the new right block becomes the right block
centreEntry.left = leftBlock;
// reduce the old block's entries into its left half of
// entries.
ArrayList<BlockEntry<K, V>> newEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = mid + 1; i < entries.size(); ++i)
newEntries.add(entries.get(i));
this.entries = newEntries;
// create a return object, with the reduced old block as the
// left block
// and the median entry with the new right block attached
SplitRootEntry<K, V> split = new SplitRootEntry<K, V>(
centreEntry, this);
// the keyed value didn't exist before , so null
return new resultAndSplit<K, V>(split, null);
}
return new resultAndSplit<K, V>(v);
}
}
V get(K k) {
if (entries.size() == 0)
return null;
BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
if (res >= 0) {
return entries.get(res).v;
}
if (index == entries.size() && rightBlock != null) {
return rightBlock.get(k);
} else if (index < entries.size()
&& entries.get(index).left != null) {
return (V) entries.get(index).left.get(k);
} else
return null;
}
void getRange(SortedMap map, K k1, K k2) {
BlockEntry<K, V> e = new BlockEntry<K, V>(k1, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
BlockEntry<K, V> e2 = new BlockEntry<K, V>(k2, null);
int res2 = Collections.binarySearch(entries, e2, cmp);
int index2 = -res2 - 1;
int from = res >= 0 ? res : index;
int to = res2 >= 0 ? res2 : index2;
for (int i = from; i <= to; ++i) {
if (i < entries.size() && (i > from || res < 0)
&& entries.get(i).left != null) {
entries.get(i).left.getRange(map, k1, k2);
// if (pc2.pos == pc.pos)
// break;
}
if (i < to || res2 >= 0)
map.put(entries.get(i).k, entries.get(i).v);
if (i == entries.size() && rightBlock != null) {
rightBlock.getRange(map, k1, k2);
}
}
}
K headKey() {
if (rightBlock != null) {
return rightBlock.headKey();
}
return entries.get(0).k;
}
K tailKey() {
int i = entries.size() - 1;
if (entries.get(i).left != null) {
return (K) entries.get(i).left.tailKey();
}
return entries.get(i).k;
}
void show(int n) {
showTabs(n);
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
System.err.print("#" + i + ":(" + e.k + ":" + e.v + ") ");
}
System.err.println();
showTabs(n);
if (rightBlock != null) {
System.err.print("Left Block\n");
rightBlock.show(n + 1);
} else {
System.err.println("No Left Block");
}
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
showTabs(n);
if (e.left != null) {
System.err.println("block right of #" + i);
e.left.show(n + 1);
} else {
System.err.println("No block right of #" + i);
}
}
showTabs(n);
System.err.println("End of Block Info\n\n");
}
private void showTabs(int n) {
// TODO Auto-generated method stub
for (int i = 0; i < n; ++i) {
System.err.print(" ");
}
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
root.getRange(map, fromKey, toKey);
return map;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
// TODO Auto-generated method stub
return subMap(root.headKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
// TODO Auto-generated method stub
return subMap(fromKey, root.tailKey());
}
@Override
public K firstKey() {
// TODO Auto-generated method stub
return root.headKey();
}
@Override
public K lastKey() {
// TODO Auto-generated method stub
return root.tailKey();
}
@Override
public int size() {
// TODO Auto-generated method stub
return 0;
}
@Override
public boolean isEmpty() {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean containsKey(Object key) {
// TODO Auto-generated method stub
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
// TODO Auto-generated method stub
return false;
}
@Override
public V get(Object key) {
// TODO Auto-generated method stub
return root.get((K) key);
}
@Override
public V put(K key, V value) {
resultAndSplit<K, V> b = root.put(key, value);
if (b.splitNode != null) {
root = new BTBlock<K, V>(root.maxSz, root.comparator);
root.rightBlock = b.splitNode.right;
root.entries.add(b.splitNode.entry);
}
return b.v;
}
@Override
public V remove(Object key) {
// TODO Auto-generated method stub
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
// TODO Auto-generated method stub
}
@Override
public void clear() {
// TODO Auto-generated method stub
}
@Override
public Set<K> keySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
public class TestBtree {
private static final int N = 50000;
public static void main(String[] args) {
BTreeMap<Integer, Integer> map = new BTreeMap<Integer , Integer>();
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
map.setComparator(comparator);
List<Integer> testVals = new ArrayList<Integer>();
for (int i =0 ; i < N ; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i ) {
int x = r.nextInt(testVals.size());
x = testVals.remove(x);
//int x=i;
t.add(x);
map.put(x, x);
}
System.err.println("output " + N + " vals");
map.root.show(0);
for (int i = 0; i < N; ++i) {
int x = t.get(i);
if ( x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("Checked " + N + " entries");
}
}
A B+ tree java example[edit | edit source]
Experiments include timing the run ( e.g. time java -cp . btreemap.BPlusTreeTest1 ) , using an external blocksize + 1 sized leaf block size, so that this is basically the underlying entries TreeMap only , vs , say, 400 internal node size, and 200 external node size . Other experiments include using a SkipListMap instead of a TreeMap.
package btreemap;
import java.util.Collection;
import java.util.Comparator;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
/**
* a B+ tree, where leaf blocks contain key-value pairs and
* internal blocks have keyed entries pointing to other internal blocks
* or leaf blocks whose keys are greater than or equal to the associated key.
*
* @author syan
*
* @param <K> key type implements Comparable
* @param <V> value type
*/
public class BPlusTreeMap<K, V> implements SortedMap<K, V> {
private int maxInternalBlockSize;
BPlusAnyBlock<K, V> root;
private int maxExternalSize;
BPlusTreeMap(int maxInternalSize, int maxExternalSize) {
this.maxInternalBlockSize = maxInternalSize;
this.maxExternalSize = maxExternalSize;
}
static class SplitOrValue<K, V> {
V v;
K k;
BPlusAnyBlock<K, V> left, right;
boolean split;
public boolean isSplit() {
return split;
}
public void setSplit(boolean split) {
this.split = split;
}
public SplitOrValue(V value) {
v = value;
setSplit(false);
}
public SplitOrValue(BPlusAnyBlock<K, V> left2,
BPlusAnyBlock<K, V> bPlusBlock) {
left = left2;
right = bPlusBlock;
k = right.firstKey();
setSplit(true);
// System.err.printf("\n\n** split occured %s**\n\n", bPlusBlock
// .getClass().getSimpleName());
}
}
static abstract class BPlusAnyBlock<K, V> {
public abstract SplitOrValue<K, V> put(K k, V v);
abstract SplitOrValue<K, V> splitBlock();
public abstract V get(K k);
public abstract boolean isEmpty();
public abstract K firstKey();
}
SortedSet<BPlusLeafBlock<K, V>> blockList = getLeafBlockSet();
SortedSet<BPlusLeafBlock<K, V>> getLeafBlockSet() {
// return new ConcurrentSkipListSet<BPlusLeafBlock<K, V>>();
return new TreeSet<BPlusLeafBlock<K, V>>();
}
static class BPlusLeafBlock<K, V> extends BPlusAnyBlock<K, V> implements
Comparable<BPlusLeafBlock<K, V>> {
SortedMap<K, V> entries = getEntryCollection();
static <K, V> SortedMap<K, V> getEntryCollection() {
return new TreeMap<K, V>();
}
int maxSize;
private BPlusTreeMap<K, V> owner;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusLeafBlock(BPlusTreeMap<K, V> bPlusTreeMap,
SortedMap<K, V> rightEntries) {
this.owner = bPlusTreeMap;
maxSize = owner.maxExternalSize;
entries = rightEntries;
}
public SplitOrValue<K, V> put(K k, V v) {
V v2 = entries.put(k, v);
if (entries.size() >= maxSize)
return splitBlock();
else
return new SplitOrValue<K, V>(v2);
}
public SplitOrValue<K, V> splitBlock() {
SortedMap<K, V> leftEntries = getEntryCollection();
SortedMap<K, V> rightEntries = getEntryCollection();
int i = 0;
for (Entry<K, V> e : entries.entrySet()) {
// System.out.println(this.getClass().getSimpleName() +
// " split entry " + e.getKey());
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
rightEntries.put(e.getKey(), e.getValue());
}
BPlusLeafBlock<K, V> right = createBlock(rightEntries);
// System.out.println("finished block split");
// System.out.println("\nleft block");
// for (K ik : leftEntries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\nright block");
// for (K ik : right.entries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private BPlusLeafBlock<K, V> createBlock(SortedMap<K, V> rightEntries) {
return owner.createLeafBlock(rightEntries);
}
@Override
public V get(K k) {
return entries.get(k);
}
@Override
public int compareTo(BPlusLeafBlock<K, V> o) {
return ((Comparable<K>) entries.firstKey()).compareTo(o.entries
.firstKey());
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
static class BPlusBranchBlock<K, V> extends BPlusAnyBlock<K, V> {
SortedMap<K, BPlusAnyBlock<K, V>> entries = createInternalBlockEntries();
int maxSize;
private BPlusAnyBlock<K, V> left;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusBranchBlock(int maxSize2) {
this.maxSize = maxSize2;
}
public SplitOrValue<K, V> put(K k, V v) {
BPlusAnyBlock<K, V> b = getBlock(k);
SplitOrValue<K, V> sv = b.put(k, v);
if (sv.isSplit()) {
entries.put(sv.k, sv.right);
if (entries.size() >= maxSize)
sv = splitBlock();
else
sv = new SplitOrValue<K, V>(null);
}
return sv;
}
BPlusAnyBlock<K, V> getBlock(K k) {
assert (entries.size() > 0);
BPlusAnyBlock<K, V> b = entries.get(k);
if (b == null) {
// headMap returns less than k
SortedMap<K, BPlusAnyBlock<K, V>> head = entries.headMap(k);
if (head.isEmpty()) {
b = left;
// System.out.println("for key " + k
// + " getting from leftmost block");
// showEntries();
} else {
b = entries.get(head.lastKey());
// System.out.println("for key " + k
// + " getting from block with key " + head.lastKey());
// showEntries();
}
}
assert (b != null);
return b;
}
public void showEntries() {
System.out.print("entries = ");
for (K k : entries.keySet()) {
System.out.print(k + " ");
}
System.out.println();
}
public SplitOrValue<K, V> splitBlock() {
Set<Entry<K, BPlusAnyBlock<K, V>>> ee = entries.entrySet();
int i = 0;
BPlusBranchBlock<K, V> right = new BPlusBranchBlock<K, V>(maxSize);
SortedMap<K, BPlusAnyBlock<K, V>> leftEntries = createInternalBlockEntries();
for (Entry<K, BPlusAnyBlock<K, V>> e : ee) {
// System.out.print("split check " + e.getKey() + ":"
// );
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
right.entries.put(e.getKey(), e.getValue());
}
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private SortedMap<K, BPlusAnyBlock<K, V>> createInternalBlockEntries() {
return new TreeMap<K, BPlusAnyBlock<K, V>>();
}
@Override
public V get(K k) {
BPlusAnyBlock<K, V> b = getBlock(k);
return b.get(k);
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
BPlusLeafBlock<K, V> b1 = getLeafBlock(fromKey);
BPlusLeafBlock<K, V> b2 = getLeafBlock(toKey);
SortedSet<BPlusLeafBlock<K, V>> range = blockList.subSet(b1, b2);
for (BPlusLeafBlock<K, V> b : range) {
SortedMap<K, V> m = b.entries.subMap(fromKey, toKey);
map.putAll(m);
}
return map;
}
private BPlusLeafBlock<K, V> getLeafBlock(K key) {
BPlusAnyBlock<K, V> b1;
b1 = root;
while (b1 instanceof BPlusBranchBlock<?, ?>) {
b1 = ((BPlusBranchBlock<K, V>) b1).getBlock(key);
}
return (BPlusLeafBlock<K, V>) b1;
}
public BPlusLeafBlock<K, V> createLeafBlock(SortedMap<K, V> rightEntries) {
BPlusLeafBlock<K, V> b = new BPlusLeafBlock<K, V>(this, rightEntries);
blockList.add(b);
return b;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
return subMap(firstKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
return subMap(fromKey, lastKey());
}
@Override
public K firstKey() {
return blockList.first().entries.firstKey();
}
@Override
public K lastKey() {
return blockList.last().entries.lastKey();
}
@Override
public int size() {
return (int) getLongSize();
}
private long getLongSize() {
long i = 0;
for (BPlusLeafBlock<K, V> b : blockList) {
i += b.entries.size();
}
return i;
}
@Override
public boolean isEmpty() {
return root.isEmpty();
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return false;
}
@Override
public V get(Object key) {
return (V) root.get((K) key);
}
@Override
public V put(K key, V value) {
if (root == null) {
SortedMap<K, V> entries = BPlusLeafBlock.getEntryCollection();
entries.put(key, value);
root = createLeafBlock(entries);
return null;
}
SplitOrValue<K, V> result = root.put(key, value);
if (result.isSplit()) {
BPlusBranchBlock<K, V> root = new BPlusBranchBlock<K, V>(
maxInternalBlockSize);
root.left = result.left;
root.entries.put(result.k, result.right);
this.root = root;
}
return result.v;
}
@Override
public V remove(Object key) {
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public void clear() {
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (BPlusLeafBlock<K, V> b : blockList) {
kk.addAll(b.entries.keySet());
}
return kk;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return null;
}
public void showLeaves() {
for (BPlusLeafBlock<K, V> b : blockList) {
System.out.println("Block");
for (Entry<K, V> e : b.entries.entrySet()) {
System.out.print(e.getKey() + ":" + e.getValue() + " ");
}
System.out.println();
}
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
/** driver program to test B+ tree */
public class BPlusTreeTest1 {
private static final int N = 1200000;
public static void main(String[] args) {
BPlusTreeMap<Integer, Integer> map = new BPlusTreeMap<Integer, Integer>(
400, 200 );// 5000002);
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
List<Integer> testVals = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i) {
int x = r.nextInt(N);
int z = testVals.set(x, testVals.get(0));
testVals.set(0, z);
}
for (int i = 0; i < N; ++i) {
map.put(testVals.get(i), testVals.get(i));
showProgress("put", testVals, i);
}
System.err.println("output " + N + " vals");
try {
for (int i = 0; i < N; ++i) {
showProgress("get", testVals, i);
int x = testVals.get(i);
if (x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("\nChecked " + N + " entries");
} catch (Exception e) {
// TODO: handle exception
e.printStackTrace();
map.showLeaves();
}
}
private static void showProgress(String label, List<Integer> testVals, int i) {
if (i % (N / 1000) == 0) {
System.out.printf("%s %d:%d; ", label, i, testVals.get(i));
if (i % (N / 10100) == 0)
System.out.println();
}
}
}
Treaps[edit | edit source]
The invariant in a binary tree is that left is less than right with respect to insertion keys. e.g. for a key with order, ord(L) < ord(R). This doesn't dictate the relationship of nodes however, and left and right rotation does not affect the above. Therefore another order can be imposed. If the order is randomised, it is likely to counteract any skewness of a plain binary tree e.g. when inserting an already sorted input in order.
Below is a java example implementation, including a plain binary tree delete code example.
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;
public class Treap1<K extends Comparable<K>, V> {
public Treap1(boolean test) {
this.test = test;
}
public Treap1() {}
boolean test = false;
static Random random = new Random(System.currentTimeMillis());
class TreapNode {
int priority = 0;
K k;
V val;
TreapNode left, right;
public TreapNode() {
if (!test) {
priority = random.nextInt();
}
}
}
TreapNode root = null;
void insert(K k, V val) {
root = insert(k, val, root);
}
TreapNode insert(K k, V val, TreapNode node) {
TreapNode node2 = new TreapNode();
node2.k = k;
node2.val = val;
if (node == null) {
node = node2;
} else if (k.compareTo(node.k) < 0) {
node.left = insert(k, val, node.left);
} else {
node.right = insert(k, val, node.right);
}
if (node.left != null && node.left.priority > node.priority) {
// left rotate
TreapNode tmp = node.left;
node.left = node.left.right;
tmp.right = node;
node = tmp;
} else if (node.right != null && node.right.priority > node.priority) {
// right rotate
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
}
return node;
}
V find(K k) {
return findNode(k, root);
}
private V findNode(K k, Treap1<K, V>.TreapNode node) {
if (node == null)
return null;
if (k.compareTo(node.k) < 0) {
return findNode(k, node.left);
} else if (k.compareTo(node.k) > 0) {
return findNode(k, node.right);
} else {
return node.val;
}
}
static class Deleted {
boolean success = false;
}
boolean delete(K k) {
Deleted del = new Deleted();
root = deleteNode(k, root, del);
return del.success;
}
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del) ;
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
public static void main(String[] args) {
LinkedList<Integer> dat = new LinkedList<Integer>();
for (int i = 0; i < 15000; ++i) {
dat.add(i);
}
testNumbers(dat, true); // no random priority balancing
testNumbers(dat, false);
}
private static void testNumbers(LinkedList<Integer> dat,
boolean test) {
Treap1<Integer, Integer> treap = new Treap1<>(test);
for (Integer integer : dat) {
treap.insert(integer, integer);
}
long t1 = System.currentTimeMillis();
Iterator<Integer> desc = dat.iterator();
int found = 0;
while (desc.hasNext()) {
Integer j = desc.next();
Integer i = treap.find(j);
if (j.equals(i)) {
++found;
}
}
long t2 = System.currentTimeMillis();
System.out.println("found = " + found + " in " + (t2 - t1));
System.out.println("test delete");
int deleted = 0;
for (Integer integer : dat) {
if (treap.delete(integer))
++deleted;
}
System.out.println("Deleted = " + deleted);
}
}
References[edit | edit source]
- William Ford and William Tapp. Data Structures with C++ using STL. 2nd ed. Upper Saddle River, NJ: Prentice Hall, 2002.
External links[edit | edit source]
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Some definitions of a heap follow:
A heap is an array , where there are parent child relationships, and the index of a child is 2 * parent index, or 2* parent index + 1 , and a child has an order after the parent, in some concrete ordering scheme injected by a client program of a heap. There is importance in maintaining the ordering n variant after the heap is changed. Some ( Sedgewick and Wayne), have coined the term "swim" and "sink", where maintenance of the invariant involves a invariant breaking item swimming up above children of lower ordering, and then sinking below any children of higher ordering, as there may be two children , so one can swim above a lower ordered child, and still have another child with higher ordering.
A heap is an efficient semi-ordered data structure for storing a collection of orderable data. A min-heap supports two operations:
INSERT(heap, element) element REMOVE_MIN(heap)
(we discuss min-heaps, but there's no real difference between min and max heaps, except how the comparison is interpreted.)
This chapter will refer exclusively to binary heaps, although different types of heaps exist. The term binary heap and heap are interchangeable in most cases. A heap can be thought of as a tree with parent and child. The main difference between a heap and a binary tree is the heap property. In order for a data structure to be considered a heap, it must satisfy the following condition (heap property):
- If A and B are elements in the heap and B is a child of A, then key(A) ≤ key(B).
(This property applies for a min-heap. A max heap would have the comparison reversed). What this tells us is that the minimum key will always remain at the top and greater values will be below it. Due to this fact, heaps are used to implement priority queues which allows quick access to the item with the most priority. Here's an example of a min-heap:

A heap is implemented using an array that is indexed from 1 to N, where N is the number of elements in the heap.
At any time, the heap must satisfy the heap property
array[n] <= array[2*n] // parent element <= left child
and
array[n] <= array[2*n+1] // parent element <= right child
whenever the indices are in the arrays bounds.
Compute the extreme value[edit | edit source]
We will prove that array[1] is the minimum element in the heap.
We prove it by seeing a contradiction if some other element is less than the first element.
Suppose array[i] is the first instance of the minimum,
with array[j] > array[i] for all j < i, and i >= 2.
But by the heap invariant array, array[floor(i/2)] <= array[i]:
this is a contradiction.
Therefore, it is easy to compute MIN(heap):
MIN(heap)
return heap.array[1];
Removing the Extreme Value[edit | edit source]
To remove the minimum element, we must adjust the heap
to fill heap.array[1]. This process is called percolation.
Basically, we move the hole from node i to either node 2i or 2i+1.
If we pick the minimum of these two, the heap invariant will be maintained;
suppose array[2i] < array[2i+1]. Then array[2i] will be moved to array[i],
leaving a hole at 2i, but after the move array[i] < array[2i+1], so the heap invariant is maintained.
In some cases, 2i+1 will exceed the array bounds, and we are forced to percolate 2i. In other cases,
2i is also outside the bounds: in that case, we are done.
Therefore, here is the remove algorithm for min heap:
#define LEFT(i) (2*i)
#define RIGHT(i) (2*i + 1)
REMOVE_MIN(heap)
{
savemin=arr[1];
arr[1]=arr[--heapsize];
i=1;
while(i<heapsize){
minidx=i;
if(LEFT(i)<heapsize && arr[LEFT(i)] < arr[minidx])
minidx=LEFT(i);
if(RIGHT(i)<heapsize && arr[RIGHT(i)] < arr[minidx])
minidx=RIGHT(i);
if(minidx!=i){
swap(arr[i],arr[minidx]);
i=minidx;
}
else
break;
}
}
Why does this work?
If there is only 1 element ,heapsize becomes 0, nothing in the array is valid. If there are 2 elements , one min and other max, you replace min with max. If there are 3 or more elements say n, you replace 0th element with n-1th element. The heap property is destroyed. Choose the 2 children of root and check which is the minimum. Choose the minimum between them, swap it. Now subtree with swapped child is loose heap property. If no violations break.
Inserting a value into the heap[edit | edit source]
A similar strategy exists for INSERT: just append the element to the array, then fixup the heap-invariants by swapping. For example if we just appended element N, then the only invariant violation possible involves that element, in particular if , then those two elements must be swapped and now the only invariant violation possible is between
array[floor(N/4)] and array[floor(N/2)]
we continue iterating until N=1 or until the invariant is satisfied.
INSERT(heap, element)
append(heap.array, element)
i = heap.array.length
while (i > 1)
{
if (heap.array[i/2] <= heap.array[i])
break;
swap(heap.array[i/2], heap.array[i]);
i /= 2;
}
TODO[edit | edit source]
Merge-heap: it would take two max/min heap and merge them and return a single heap. O(n) time. Make-heap: it would also be nice to describe the O(n) make-heap operation Heap sort: the structure can actually be used to efficiently sort arrays
Make-heap would make use a function heapify
//Element is a data structure//
Make-heap(Element Arr[],int size)
{
for(j=size/2;j>0;j--)
{
Heapify(Arr,size,j);
}
}
Heapify(Element Arr[],int size,int t)
{
L=2*t;
R=2*t+1;
if(L<size )
{
mix=minindex(Arr,L,t);
if(R<=size)
mix=minindex(Arr,R,mix);
}
else
mix=t;
if(mix!=t)
{
swap(mix,t);
Heapify(Arr,size,mix);
}
}
minindex returns index of the smaller element
Applications of Priority Heaps[edit | edit source]
In 2009, a smaller Sort Benchmark was won by OzSort, which has a paper describing lucidly how to use a priority heap as the sorting machine to produce merged parts of large (internally) sorted sections . If a sorted section took M memory and the sorting problem was k x M big, then take sequential sections of each of the k sections of size M/k , at a time, so they fit in M memory ( k * M/k = M ), and feed the first element of each of k sections to make a k sized priority queue, and as the top element is removed and written to an output buffer, take the next element from the corresponding section. This means elements may need to be associated with a label for the section they come from. When a M/k-sized section is exhausted, load in the next M/k sized minisection from the original sorted section stored on disc. Continue until all minisections in each of the k sections on disc have been exhausted.
(As an example of pipelining to fill up disc operational delays, there are twin output buffers, so that once an output buffer is full one gets written the disc while the other is being filled.)
This paper showed that a priority heap is more straightforward than a binary tree, because elements are constantly being deleted, as well as added, as a queuing mechanism for a k way merge, and has practical application for sorting large sets of data that exceed internal memory storage.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Graphs[edit | edit source]
A graph is a structure consisting of a set of vertices and a set of edges . An edge is a pair of vertices . The two vertices are called the edge endpoints. Graphs are ubiquitous in computer science. They are used to model real-world systems such as the Internet (each node represents a router and each edge represents a connection between routers); airline connections (each node is an airport and each edge is a flight); or a city road network (each node represents an intersection and each edge represents a block). The wireframe drawings in computer graphics are another example of graphs.
A graph may be either undirected or directed. Intuitively, an undirected edge models a "two-way" or "duplex" connection between its endpoints, while a directed edge is a one-way connection, and is typically drawn as an arrow. A directed edge is often called an arc. Mathematically, an undirected edge is an unordered pair of vertices, and an arc is an ordered pair. For example, a road network might be modeled as a directed graph, with one-way streets indicated by an arrow between endpoints in the appropriate direction, and two-way streets shown by a pair of parallel directed edges going both directions between the endpoints. You might ask, why not use a single undirected edge for a two-way street. There's no theoretical problem with this, but from a practical programming standpoint, it's generally simpler and less error-prone to stick with all directed or all undirected edges.
An undirected graph can have at most edges (one for each unordered pair), while a directed graph can have at most edges (one per ordered pair). A graph is called sparse if it has many fewer than this many edges (typically edges), and dense if it has closer to edges. A multigraph can have more than one edge between the same two vertices. For example, if one were modeling airline flights, there might be multiple flights between two cities, occurring at different times of the day.
A path in a graph is a sequence of vertices such that there exists an edge or arc between consecutive vertices. The path is called a cycle if . An undirected acyclic graph is equivalent to an undirected tree. A directed acyclic graph is called a DAG. It is not necessarily a tree.
Nodes and edges often have associated information, such as labels or weights. For example, in a graph of airline flights, a node might be labeled with the name of the corresponding airport, and an edge might have a weight equal to the flight time. The popular game "Six Degrees of Kevin Bacon" can be modeled by a labeled undirected graph. Each actor becomes a node, labeled by the actor's name. Nodes are connected by an edge when the two actors appeared together in some movie. We can label this edge by the name of the movie. Deciding if an actor is separated from Kevin Bacon by six or fewer steps is equivalent to finding a path of length at most six in the graph between Bacon's vertex and the other actors vertex. (This can be done with the breadth-first search algorithm found in the companion Algorithms book. The Oracle of Bacon at the University of Virginia has actually implemented this algorithm and can tell you the path from any actor to Kevin Bacon in a few clicks[1].)
Directed Graphs[edit | edit source]
The number of edges with one endpoint on a given vertex is called that vertex's degree. In a directed graph, the number of edges that point to a given vertex is called its in-degree, and the number that point from it is called its out-degree. Often, we may want to be able to distinguish between different nodes and edges. We can associate labels with either. We call such a graph labeled.
Directed Graph Operations
make-graph(): graph- Create a new graph, initially with no nodes or edges.
make-vertex(graph G, element value): vertex- Create a new vertex, with the given value.
make-edge(vertex u, vertex v): edge- Create an edge between u and v. In a directed graph, the edge will flow from u to v.
get-edges(vertex v): edge-set- Returns the set of edges flowing from v
get-neighbors(vertex v): vertex-set- Returns the set of vertices connected to v
Undirected Graphs[edit | edit source]

In a directed graph, the edges point from one vertex to another, while in an undirected graph, they merely connect two vertices. we can travel forward or backward.It is a bidirectional graph.
Weighted Graphs[edit | edit source]
We may also want to associate some cost or weight to the traversal of an edge. When we add this information, the graph is called weighted. An example of a weighted graph would be the distance between the capitals of a set of countries.
Directed and undirected graphs may both be weighted. The operations on a weighted graph are the same with addition of a weight parameter during edge creation:
Weighted Graph Operations (an extension of undirected/directed graph operations)
make-edge(vertex u, vertex v, weight w): edge- Create an edge between u and v with weight w. In a directed graph, the edge will flow from u to v.
Graph Representations[edit | edit source]
Adjacency Matrix Representation[edit | edit source]
An adjacency matrix is one of the two common ways to represent a graph. The adjacency matrix shows which nodes are adjacent to one another. Two nodes are adjacent if there is an edge connecting them. In the case of a directed graph, if node is adjacent to node , there is an edge from to . In other words, if is adjacent to , you can get from to by traversing one edge. For a given graph with nodes, the adjacency matrix will have dimensions of . For an unweighted graph, the adjacency matrix will be populated with boolean values.
For any given node , you can determine its adjacent nodes by looking at row of the adjacency matrix. A value of true at indicates that there is an edge from node to node , and false indicating no edge. In an undirected graph, the values of and will be equal. In a weighted graph, the boolean values will be replaced by the weight of the edge connecting the two nodes, with a special value that indicates the absence of an edge.
The memory use of an adjacency matrix is .
Adjacency List Representation[edit | edit source]
The adjacency list is another common representation of a graph. There are many ways to implement this adjacency representation. One way is to have the graph maintain a list of lists, in which the first list is a list of indices corresponding to each node in the graph. Each of these refer to another list that stores the index of each adjacent node to this one. It might also be useful to associate the weight of each link with the adjacent node in this list.
Example: An undirected graph contains four nodes 1, 2, 3 and 4. 1 is linked to 2 and 3. 2 is linked to 3. 3 is linked to 4.
1 - [2, 3]
2 - [1, 3]
3 - [1, 2, 4]
4 - [3]
It might be useful to store the list of all the nodes in the graph in a hash table. The keys then would correspond to the indices of each node and the value would be a reference to the list of adjacent node indices.
Another implementation might require that each node keep a list of its adjacent nodes.
Graph Traversals[edit | edit source]
In a perfect world we would have full knowledge of the graph's contents, letting us optimize indices for the vertices and edges for efficient look-ups. But there are numerous open-ended problems in computer science where indexing is impractical or even impossible. Graph traversals let us tackle these problems. The traversals let us efficiently search large spaces where objects are defined by their relationships to other objects rather than properties of the objects themselves.
Depth-First Search[edit | edit source]
Start at vertex a, visit its neighbour b, then b's neighbour c and keep going until reach 'a dead end' then iterate back and visit nodes reachable from second last visited vertex and keep applying the same principle.
// Search in the subgraph for a node matching 'criteria'. Do not re-examine
// nodes listed in 'visited' which have already been tested.
GraphNode depth_first_search(GraphNode node, Predicate criteria, VisitedSet visited) {
// Check that we haven't already visited this part of the graph
if (visited.contains(node)) {
return null;
}
visited.insert(node);
// Test to see if this node satisfies the criteria
if (criteria.apply(node.value)) {
return node;
}
// Search adjacent nodes for a match
for (adjacent in node.adjacentnodes()) {
GraphNode ret = depth_first_search(adjacent, criteria, visited);
if (ret != null) {
return ret;
}
}
// Give up - not in this part of the graph
return null;
}
Breadth-First Search[edit | edit source]
Breadth first search visits the nodes neighbours and then the unvisited neighbours of the neighbours, etc. If it starts on vertex a it will go to all vertices that have an edge from a. If some points are not reachable it will have to start another BFS from a new vertex.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Hash Tables[edit | edit source]
A hash table, or a hash map, is a data structure that associates keys with values. The primary operation it supports efficiently is a lookup: given a key (e.g. a person's name), find the corresponding value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that the hash table uses to locate the desired value. This hash maps directly to a bucket in the array of key/value pairs, hence the name hash map. The mapping method lets us directly access the storage location for any key/value pair.
Hash table<Element> Operations
make-hash-table(integer n): HashTable
- Create a hash table with n buckets.
get-value(HashTable h, Comparable key): Element
- Returns the value of the element for the given key. The key must be some comparable type.
set-value(HashTable h, Comparable key, Element new-value)
- Sets the element of the array for the given key to be equal to new-value. The key must be some comparable type.
remove(HashTable h, Comparable key)
- Remove the element for the given key from the hash table. The key must be some comparable type.

Time complexity and common uses of hash tables[edit | edit source]
Hash tables are often used to implement associative arrays, sets and caches. Like arrays, hash tables provide constant-time O(1) lookup on average, regardless of the number of items in the table. The (hopefully rare) worst-case lookup time in most hash table schemes is O(n).[1] Compared to other associative array data structures, hash tables are most useful when we need to store a large numbers of data records.
Hash tables may be used as in-memory data structures. Hash tables may also be adopted for use with persistent data structures; database indexes commonly use disk-based data structures based on hash tables.
Hash tables are also used to speed-up string searching in many implementations of data compression.
In computer chess, a hash table can be used to implement the transposition table.
Choosing a good hash function[edit | edit source]
A good hash function is essential for good hash table performance. A poor choice of hash function is likely to lead to clustering behavior, in which the probability of keys mapping to the same hash bucket (i.e. a collision) is significantly greater than would be expected from a random function. A nonzero probability of collisions is inevitable in any hash implementation, but the number of operations to resolve collisions usually scales linearly with the number of keys mapping to the same bucket, so excess collisions will degrade performance significantly. In addition, some hash functions are computationally expensive, so the amount of time (and, in some cases, memory) taken to compute the hash may be burdensome.
Choosing a good hash function is tricky. The literature is replete with poor choices, at least when measured by modern standards. For example, the very popular multiplicative hash advocated by Knuth in The Art of Computer Programming (see reference below) has particularly poor clustering behavior. However, since poor hashing merely degrades hash table performance for particular input key distributions, such problems go undetected far too often.
The literature is also sparse on the criteria for choosing a hash function. Unlike most other fundamental algorithms and data structures, there is no universal consensus on what makes a "good" hash function. The remainder of this section is organized by three criteria: simplicity, speed, and strength, and will survey algorithms known to perform well by these criteria.
Simplicity and speed are readily measured objectively (by number of lines of code and CPU benchmarks, for example), but strength is a more slippery concept. Obviously, a cryptographic hash function such as SHA-1 would satisfy the relatively lax strength requirements needed for hash tables, but their slowness and complexity makes them unappealing. In fact, even a cryptographic hash does not provide protection against an adversary who wishes to degrade hash table performance by choosing keys all hashing to the same bucket. For these specialized cases, a universal hash function should be used instead of any one static hash, no matter how sophisticated.
In the absence of a standard measure for hash function strength, the current state of the art is to employ a battery of statistical tests to measure whether the hash function can be readily distinguished from a random function. Arguably the most important such test is to determine whether the hash function displays the avalanche effect, which essentially states that any single-bit change in the input key should affect on average half the bits in the output. Bret Mulvey advocates testing the strict avalanche condition in particular, which states that, for any single-bit change, each of the output bits should change with probability one-half, independent of the other bits in the key. Purely additive hash functions such as CRC fail this stronger condition miserably.
Clearly, a strong hash function should have a uniform distribution of hash values. Bret Mulvey proposes the use of a chi-squared test for uniformity, based on power of two hash table sizes ranging from 21 to 216. This test is considerably more sensitive than many others proposed for measuring hash functions, and finds problems in many popular hash functions.
Fortunately, there are good hash functions that satisfy all these criteria. The simplest class all consume one byte of the input key per iteration of the inner loop. Within this class, simplicity and speed are closely related, as fast algorithms simply don't have time to perform complex calculations. Of these, one that performs particularly well is the Jenkins One-at-a-time hash, adapted here from an article by Bob Jenkins, its creator.
uint32 joaat_hash(uchar *key, size_t len)
{
uint32 hash = 0;
size_t i;
for (i = 0; i < len; i++)
{
hash += key[i];
hash += (hash << 10);
hash ^= (hash >> 6);
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}

The avalanche behavior of this hash shown on the right. The image was made using Bret Mulvey's AvalancheTest in his Hash.cs toolset. Each row corresponds to a single bit in the input, and each column to a bit in the output. A green square indicates good mixing behavior, a yellow square weak mixing behavior, and red would indicate no mixing. Only a few bits in the last byte are weakly mixed, a performance vastly better than a number of widely used hash functions.
Many commonly used hash functions perform poorly when subjected to such rigorous avalanche testing. The widely favored FNV hash, for example, shows many bits with no mixing at all, especially for short keys. See the evaluation of FNV by Bret Mulvey for a more thorough analysis.
If speed is more important than simplicity, then the class of hash functions which consume multibyte chunks per iteration may be of interest. One of the most sophisticated is "lookup3" by Bob Jenkins, which consumes input in 12 byte (96 bit) chunks. Note, though, that any speed improvement from the use of this hash is only likely to be useful for large keys, and that the increased complexity may also have speed consequences such as preventing an optimizing compiler from inlining the hash function. Bret Mulvey analyzed an earlier version, lookup2, and found it to have excellent avalanche behavior.
One desirable property of a hash function is that conversion from the hash value (typically 32 bits) to an bucket index for a particular-size hash table can be done simply by masking, preserving only the lower k bits for a table of size 2k (an operation equivalent to computing the hash value modulo the table size). This property enables the technique of incremental doubling of the size of the hash table - each bucket in the old table maps to only two in the new table. Because of its use of XOR-folding, the FNV hash does not have this property. Some older hashes are even worse, requiring table sizes to be a prime number rather than a power of two, again computing the bucket index as the hash value modulo the table size. In general, such a requirement is a sign of a fundamentally weak function; using a prime table size is a poor substitute for using a stronger function.
Collision resolution[edit | edit source]
If two keys hash to the same index, the corresponding records cannot be stored in the same location. So, if it's already occupied, we must find another location to store the new record, and do it so that we can find it when we look it up later on.
To give an idea of the importance of a good collision resolution strategy, consider the following result, derived using the birthday paradox. Even if we assume that our hash function outputs random indices uniformly distributed over the array, and even for an array with 1 million entries, there is a 95% chance of at least one collision occurring before it contains 2500 records.
There are a number of collision resolution techniques, but the most popular are chaining and open addressing.
Chaining[edit | edit source]
In the simplest chained hash table technique, each slot in the array references a linked list of inserted records that collide to the same slot. Insertion requires finding the correct slot, and appending to either end of the list in that slot; deletion requires searching the list and removal.
Chained hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.
Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.
Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance when records are small.
Some chaining implementations use an optimization where the first record of each chain is stored in the table. Although this can increase performance, it is generally not recommended: chaining tables with reasonable load factors contain a large proportion of empty slots, and the larger slot size causes them to waste large amounts of space.
Open addressing[edit | edit source]

Open addressing hash tables can store the records directly within the array. A hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:
- linear probing
- in which the interval between probes is fixed—often at 1,
- quadratic probing
- in which the interval between probes increases linearly (hence, the indices are described by a quadratic function), and
- double hashing
- in which the interval between probes is fixed for each record but is computed by another hash function.
The main tradeoffs between these methods are that linear probing has the best cache performance but is most sensitive to clustering, while double hashing has poor cache performance but exhibits virtually no clustering; quadratic hashing falls in-between in both areas. Double hashing can also require more computation than other forms of probing. Some open addressing methods, such as last-come-first-served hashing and cuckoo hashing move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing.
A critical influence on performance of an open addressing hash table is the load factor; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering.
Example pseudocode[edit | edit source]
The following pseudocode is an implementation of an open addressing hash table with linear probing and single-slot stepping, a common approach that is effective if the hash function is good. Each of the lookup, set and remove functions use a common internal function findSlot to locate the array slot that either does or should contain a given key.
record pair { key, value }
var pair array slot[0..numSlots-1]
function findSlot(key)
i := hash(key) modulus numSlots
loop
if slot[i] is not occupied or slot[i].key = key
return i
i := (i + 1) modulus numSlots
function lookup(key)
i := findSlot(key)
if slot[i] is occupied // key is in table
return slot[i].value
else // key is not in table
return not found
function set(key, value)
i := findSlot(key)
if slot[i].key = key
// (Key already in table. Update value.)
slot[i].value := value
else
// (Insert key and value in un-occupied slot.)
// (But first, make sure insert won't overload the table)
if the table is almost full
rebuild the table larger (note 1)
i := findSlot(key)
slot[i].key := key
slot[i].value := value
Another example showing open addressing technique. Presented function is converting each part(4) of an Internet protocol address, where NOT is bitwise NOT, XOR is bitwise XOR, OR is bitwise OR, AND is bitwise AND and << and >> are shift-left and shift-right:
// key_1,key_2,key_3,key_4 are following 3-digit numbers - parts of ip address xxx.xxx.xxx.xxx
function ip(key parts)
j := 1
do
key := (key_2 << 2)
key := (key + (key_3 << 7))
key := key + (j OR key_4 >> 2) * (key_4) * (j + key_1) XOR j
key := key AND _prime_ // _prime_ is a prime number
j := (j+1)
while collision
return key
- note 1
- Rebuilding the table requires allocating a larger array and recursively using the set operation to insert all the elements of the old array into the new larger array. It is common to increase the array size exponentially, for example by doubling the old array size.
function remove(key)
i := findSlot(key)
if slot[i] is unoccupied
return // key is not in the table
j := i
loop
j := (j+1) modulus numSlots
if slot[j] is unoccupied
exit loop
k := hash(slot[j].key) modulus numSlots
if (j > i and (k <= i or k > j)) or
(j < i and (k <= i and k > j)) (note 2)
slot[i] := slot[j]
i := j
mark slot[i] as unoccupied
- note 2
- For all records in a cluster, there must be no vacant slots between their natural hash position and their current position (else lookups will terminate before finding the record). At this point in the pseudocode, i is a vacant slot that might be invalidating this property for subsequent records in the cluster. j is such as subsequent record. k is the raw hash where the record at j would naturally land in the hash table if there were no collisions. This test is asking if the record at j is invalidly positioned with respect to the required properties of a cluster now that i is vacant.
Another technique for removal is simply to mark the slot as deleted. However this eventually requires rebuilding the table simply to remove deleted records. The methods above provide O(1) updating and removal of existing records, with occasional rebuilding if the high water mark of the table size grows.
The O(1) remove method above is only possible in linearly probed hash tables with single-slot stepping. In the case where many records are to be deleted in one operation, marking the slots for deletion and later rebuilding may be more efficient.
Open addressing versus chaining[edit | edit source]
Chained hash tables have the following benefits over open addressing:
- They are simple to implement effectively and only require basic data structures.
- From the point of view of writing suitable hash functions, chained hash tables are insensitive to clustering, only requiring minimization of collisions. Open addressing depends upon better hash functions to avoid clustering. This is particularly important if novice programmers can add their own hash functions, but even experienced programmers can be caught out by unexpected clustering effects.
- They degrade in performance more gracefully. Although chains grow longer as the table fills, a chained hash table cannot "fill up" and does not exhibit the sudden increases in lookup times that occur in a near-full table with open addressing. (see right)
- If the hash table stores large records, about 5 or more words per record, chaining uses less memory than open addressing.
- If the hash table is sparse (that is, it has a big array with many free array slots), chaining uses less memory than open addressing even for small records of 2 to 4 words per record due to its external storage.

For small record sizes (a few words or less) the benefits of in-place open addressing compared to chaining are:
- They can be more space-efficient than chaining since they don't need to store any pointers or allocate any additional space outside the hash table. Simple linked lists require a word of overhead per element.
- Insertions avoid the time overhead of memory allocation, and can even be implemented in the absence of a memory allocator.
- Because it uses internal storage, open addressing avoids the extra indirection required for chaining's external storage. It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.
- They can be easier to serialize, because they don't use pointers.
On the other hand, normal open addressing is a poor choice for large elements, since these elements fill entire cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.
Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. In cases where the tables are expected to have high load factors, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.
Ultimately, used sensibly any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms is marginal, and other considerations typically come into play.
Coalesced hashing[edit | edit source]
A hybrid of chaining and open addressing, coalesced hashing links together chains of nodes within the table itself. Like open addressing, it achieves space usage and (somewhat diminished) cache advantages over chaining. Like chaining, it does not exhibit clustering effects; in fact, the table can be efficiently filled to a high density. Unlike chaining, it cannot have more elements than table slots.
Perfect hashing[edit | edit source]
If all of the keys that will be used are known ahead of time, and there are no more keys that can fit the hash table, perfect hashing can be used to create a perfect hash table, in which there will be no collisions. If minimal perfect hashing is used, every location in the hash table can be used as well.
Perfect hashing gives a hash table where the time to make a lookup is constant in the worst case. This is in contrast to chaining and open addressing methods, where the time for lookup is low on average, but may be arbitrarily large. There exist methods for maintaining a perfect hash function under insertions of keys, known as dynamic perfect hashing. A simpler alternative, that also gives worst case constant lookup time, is cuckoo hashing.
Probabilistic hashing[edit | edit source]
Perhaps the simplest solution to a collision is to replace the value that is already in the slot with the new value, or slightly less commonly, drop the record that is to be inserted. In later searches, this may result in a search not finding a record which has been inserted. This technique is particularly useful for implementing caching.
An even more space-efficient solution which is similar to this is use a bit array (an array of one-bit fields) for our table. Initially all bits are set to zero, and when we insert a key, we set the corresponding bit to one. False negatives cannot occur, but false positives can, since if the search finds a 1 bit, it will claim that the value was found, even if it was just another value that hashed into the same array slot by coincidence. In reality, such a hash table is merely a specific type of Bloom filter.
Table resizing[edit | edit source]
With a good hash function, a hash table can typically contain about 70%–80% as many elements as it does table slots and still perform well. Depending on the collision resolution mechanism, performance can begin to suffer either gradually or dramatically as more elements are added. To deal with this, when the load factor exceeds some threshold, we allocate a new, larger table, and add all the contents of the original table to this new table. In Java's HashMap class, for example, the default load factor threshold is 0.75.
This can be a very expensive operation, and the necessity for it is one of the hash table's disadvantages. In fact, some naive methods for doing this, such as enlarging the table by one each time you add a new element, reduce performance so drastically as to make the hash table useless. However, if we enlarge the table by some fixed percent, such as 10% or 100%, it can be shown using amortized analysis that these resizings are so infrequent that the average time per lookup remains constant-time. To see why this is true, suppose a hash table using chaining begins at the minimum size of 1 and is doubled each time it fills above 100%. If in the end it contains n elements, then the total add operations performed for all the resizings is:
- 1 + 2 + 4 + ... + n = 2n - 1.
Because the costs of the resizings form a geometric series, the total cost is O(n). But we also perform n operations to add the n elements in the first place, so the total time to add n elements with resizing is O(n), an amortized time of O(1) per element.
On the other hand, some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. One simple approach is to initially allocate the table with enough space for the expected number of elements and forbid the addition of too many elements. Another useful but more memory-intensive technique is to perform the resizing gradually:
- Allocate the new hash table, but leave the old hash table and check both tables during lookups.
- Each time an insertion is performed, add that element to the new table and also move k elements from the old table to the new table.
- When all elements are removed from the old table, deallocate it.
To ensure that the old table will be completely copied over before the new table itself needs to be enlarged, it's necessary to increase the size of the table by a factor of at least (k + 1)/k during the resizing.
Linear hashing is a hash table algorithm that permits incremental hash table expansion. It is implemented using a single hash table, but with two possible look-up functions.
Another way to decrease the cost of table resizing is to choose a hash function in such a way that the hashes of most values do not change when the table is resized. This approach, called consistent hashing, is prevalent in disk-based and distributed hashes, where resizing is prohibitively costly.
Ordered retrieval issue[edit | edit source]
Hash tables store data in pseudo-random locations, so accessing the data in a sorted manner is a very time consuming operation. Other data structures such as self-balancing binary search trees generally operate more slowly (since their lookup time is O(log n)) and are rather more complex to implement than hash tables but maintain a sorted data structure at all times. See a comparison of hash tables and self-balancing binary search trees.
Problems with hash tables[edit | edit source]
Although hash table lookups use constant time on average, the time spent can be significant. Evaluating a good hash function can be a slow operation. In particular, if simple array indexing can be used instead, this is usually faster.
Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays. Compact data structures such as arrays, searched with linear search, may be faster if the table is relatively small and keys are cheap to compare, such as with simple integer keys. According to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimal performance point varies from system to system; for example, a trial on Parrot shows that its hash tables outperform linear search in all but the most trivial cases (one to three entries).
More significantly, hash tables are more difficult and error-prone to write and use. Hash tables require the design of an effective hash function for each key type, which in many situations is more difficult and time-consuming to design and debug than the mere comparison function required for a self-balancing binary search tree. In open-addressed hash tables it's even easier to create a poor hash function.
Additionally, in some applications, a black hat with knowledge of the hash function may be able to supply information to a hash which creates worst-case behavior by causing excessive collisions, resulting in very poor performance (i.e., a denial of service attack). In critical applications, either universal hashing can be used or a data structure with better worst-case guarantees may be preferable. For details, see Crosby and Wallach's Denial of Service via Algorithmic Complexity Attacks.
Other hash table algorithms[edit | edit source]
Extendible hashing and linear hashing are hash algorithms that are used in the context of database algorithms used for instance in index file structures, and even primary file organization for a database. Generally, in order to make search scalable for large databases, the search time should be proportional log N or near constant, where N is the number of records to search. Log N searches can be implemented with tree structures, because the degree of fan out and the shortness of the tree relates to the number of steps needed to find a record, so the height of the tree is the maximum number of disc accesses it takes to find where a record is. However, hash tables are also used, because the cost of a disk access can be counted in units of disc accesses, and often that unit is a block of data. Since a hash table can, in the best case, find a key with one or two accesses, a hash table index is regarded as generally faster when retrieving a collection of records during a join operation e.g.
SELECT * from customer, orders where customer.cust_id = orders.cust_id and cust_id = X
i.e. If orders has a hash index on cust_id, then it takes constant time to locate the block that contains record locations for orders matching cust_id = X. (although, it would be better if the value type of orders was a list of order ids, so that hash keys are just one unique cust_id for each batch of orders, to avoid unnecessary collisions).
Extendible hashing and linear hashing have certain similarities: collisions are accepted as inevitable and are part of the algorithm where blocks or buckets of collision space is added ; traditional good hash function ranges are required, but the hash value is transformed by a dynamic address function : in extendible hashing, a bit mask is used to mask out unwanted bits, but this mask length increases by one periodically, doubling the available addressing space ; also in extendible hashing, there is an indirection with a directory address space, the directory entries being paired with another address (a pointer ) to the actual block containing the key-value pairs; the entries in the directory correspond to the bit masked hash value (so that the number of entries is equal to maximum bit mask value + 1 e.g. a bit mask of 2 bits, can address a directory of 00 01 10 11, or 3 + 1 = 4).
In linear hashing, the traditional hash value is also masked with a bit mask, but if the resultant smaller hash value falls below a 'split' variable, the original hash value is masked with a bit mask of one bit greater length, making the resultant hash value address recently added blocks. The split variable ranges incrementally between 0 and the maximum current bit mask value e.g. a bit mask of 2, or in the terminology of linear hashing, a "level" of 2, the split variable will range between 0 and 3. When the split variable reaches 4, the level increases by 1, so in the next round of the split variable, it will range between 0 and 7, and reset again when it reaches 8.
The split variable incrementally allows increased addressing space, as new blocks are added; the decision to add a new block occurs whenever a key-and=value is being inserted, and overflows the particular block the key-and-value's key hashes into. This overflow location may be completely unrelated to the block going to be split pointed to by the split variable. However, over time, it is expected that given a good random hash function that distributes entries fairly evenly amongst all addressable blocks, the blocks that actually require splitting because they have overflowed get their turn in round-robin fashion as the split value ranges between 0 - N where N has a factor of 2 to the power of Level, level being the variable incremented whenever the split variable hits N.
New blocks are added one at a time with both extendible hashing, and with linear hashing.
In extendible hashing, a block overflow ( a new key-value colliding with B other key-values, where B is the size of a block) is handled by checking the size of the bit mask "locally", called the "local depth", an attribute which must be stored with the block. The directory structure, also has a depth, the "global depth". If the local depth is less than the global depth, then the local depth is incremented, and all the key values are rehashed and passed through a bit mask which is one bit longer now, placing them either in the current block, or in another block. If the other block happens to be the same block when looked up in the directory, a new block is added, and the directory entry for the other block is made to point to the new block. Why does the directory have entries where two entries point to the same block ? This is because if the local depth is equal to the global depth of the directory, this means the bit mask of the directory does not have enough bits to deal with an increment in the bit mask length of the block, and so the directory must have its bit mask length incremented, but this means the directory now doubles the number of addressable entries. Since half the entries addressable don't exist, the directory simply copies the pointers over to the new entries e.g. if the directory had entries for 00, 01, 10, 11, or a 2 bit mask, and it becomes a 3 bit mask, then 000 001 010 011 100 101 110 111 become the new entries, and 00's block address go to 000 and 001 ; 01's pointer goes to 010 and 011, 10 goes to 100 and 101 and so on. And so this creates the situation where two directory entries point to the same block. Although the block that was going to overflow, now can add a new block by redirecting the second pointer to a newly appended block, the other original blocks will have two pointers to them. When it is their turn to split, the algorithm will check local vs global depth and this time find that the local depth is less, and hence no directory splitting is required, only a new block be appended, and the second directory pointer moved from addressing the previous block to addressing the new block.
In linear hashing, adding a similarly hashed block does not occurs immediately when a block overflows, and therefore an overflow block is created to be attached to the overflowing block. However, a block overflow is a signal that more space will be required, and this happens by splitting the block pointed to by the "split" variable, which is initially zero, and hence initially points to block zero. The splitting is done by taking all the key-value pairs in the splitting block, and its overflow block(s), hashing the keys again, but with a bit mask of length current level + 1. This will result in two block addresses, some will be the old block number, and others will be
a2 = old block number + ( N times 2 ^ (level) )
- Rationale
Let m = N times 2 ^ level ; if h is the original hash value, and old block number = h mod m, and now the new block number is h mod ( m * 2 ), because m * 2 = N times 2 ^ (level+1), then the new block number is either h mod m if (h / m) is even so dividing h/m by 2 leaves a zero remainder and therefore doesn't change the remainder, or the new block number is ( h mod m ) + m because h / m is an odd number, and dividing h / m by 2 will leave an excess remainder of m, + the original remainder. ( The same rationale applies to extendible hashing depth incrementing ).
As above, a new block is created with a number a2, which will usually occur at +1 the previous a2 value. Once this is done, the split variable is incremented, so that the next a2 value will be again old a2 + 1. In this way, each block is covered by the split variable eventually, so each block is preemptively rehashed into extra space, and new blocks are added incrementally. Overflow blocks that are no longer needed are discarded, for later garbage collection if needed, or put on an available free block list by chaining.
When the split variable reaches ( N times 2 ^ level ), level is incremented and split variable is reset to zero. In this next round, the split variable will now traverse from zero to ( N times 2 ^ (old_level + 1 ) ), which is exactly the number of blocks at the start of the previous round, but including all the blocks created by the previous round.
A simple inference on file storage mapping of linear hashing and extendible hashing[edit | edit source]
As can be seen, extendible hashing requires space to store a directory which can double in size.
Since the space of both algorithms increase by one block at a time, if blocks have a known maximum size or fixed size, then it is straight forward to map the blocks as blocks sequentially appended to a file.
In extendible hashing, it would be logical to store the directory as a separate file, as doubling can be accommodated by adding to the end of the directory file. The separate block file would not have to change, other than have blocks appended to its end.
Header information for linear hashing doesn't increase in size : basically just the values for N, level, and split need to be recorded, so these can be incorporated as a header into a fixed block size linear hash storage file.
However, linear hashing requires space for overflow blocks, and this might best be stored in another file, otherwise addressing blocks in the linear hash file is not as straight forward as multiplying the block number by the block size and adding the space for N,level, and split.
In the next section, a complete example of linear hashing in Java is given, using a in memory implementation of linear hashing, and code to manage blocks as files in a file directory, the whole contents of the file directory representing the persistent linear hashing structure.
Implementations[edit | edit source]
While many programming languages already provide hash table functionality,[2] there are several independent implementations worth mentioning.
- Google Sparse Hash The Google SparseHash project contains several hash-map implementations in use at Google, with different performance characteristics, including an implementation that optimizes for space and one that optimizes for speed. The memory-optimized one is extremely memory-efficient with only 2 bits/entry of overhead.
- MCT provides hashtables similar to Google's
dense_hash_map, but without restriction on contained values; it also comes with exception safety and support for C++0x features. - A number of runtime languages and/or standard libraries use hash tables to implement their support for associative arrays because of their efficiency.
A python implementation of extendible hashing[edit | edit source]
The file - block management routines aren't there, so this could be added in to make this a real implementation of a database hash index.
A full page is split according to the (local depth)th bit, first by collecting all the directory indices pointing to the full page, updating the pointers according to the d bit being 0 or 1 corresponding to first and second new pages, then reloading all the key-values after hashing each key and using the d bit of each hash to see which page to allocate to. The local depth of each new page is one greater than the old page's local depth, so that the next d bit can be used next time when splitting.
PAGE_SZ = 20
class Page:
def __init__(self):
self.m = {}
self.d = 0
def full(self):
return len(self.m) > PAGE_SZ
def put(self,k,v):
self.m[k] = v
def get(self,k):
return self.m.get(k)
class EH:
def __init__(self):
self.gd = 0
p = Page()
self.pp= [p]
def get_page(self,k):
h = hash(k)
p = self.pp[ h & (( 1 << self.gd) -1)]
return p
def put(self, k, v):
p = self.get_page(k)
if p.full() and p.d == self.gd:
self.pp = self.pp + self.pp
self.gd += 1
if p.full() and p.d < self.gd:
p.put(k,v);
p1 = Page()
p2 = Page()
for k2 in p.m.keys():
v2 = p.m[k2]
h = k2.__hash__()
h = h & ((1 << self.gd) -1)
if (h | (1 << p.d) == h):
p2.put(k2,v2)
else:
p1.put(k2,v2)
l = []
for i in xrange(0, len(self.pp)):
if self.pp[i] == p:
l.append(i)
for i in l:
if (i | ( 1 << p.d) == i):
self.pp[i] = p2
else:
self.pp[i] = p1
p1.d = p.d + 1
p2.d = p1.d
else:
p.put(k, v)
def get(self, k):
p = self.get_page(k)
return p.get(k)
if __name__ == "__main__":
eh = EH()
N = 10000
l = []
for i in range(0,N):
l.append(i)
import random
random.shuffle(l)
for i in l:
eh.put(i,i)
print l
for i in range(0, N):
print eh.get(i)
A Java implementation of extendible hashing[edit | edit source]
A direct Java translation of the above python code, tested to work.
package ext_hashing;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
public class EH2<K, V> {
static class Page<K, V> {
static int PAGE_SZ = 20;
private Map<K, V> m = new HashMap<K, V>();
int d = 0;
boolean full() {
return m.size() > PAGE_SZ;
}
void put(K k, V v) {
m.put(k, v);
}
V get(K k) {
return m.get(k);
}
}
int gd = 0;
List<Page<K, V>> pp = new ArrayList<Page<K, V>>();
public EH2() {
pp.add(new Page<K, V>());
}
Page<K, V> getPage(K k) {
int h = k.hashCode();
Page<K, V> p = pp.get(h & ((1 << gd) - 1));
return p;
}
void put(K k, V v) {
Page<K, V> p = getPage(k);
if (p.full() && p.d == gd) {
List<Page<K, V>> pp2 = new ArrayList<EH2.Page<K, V>>(pp);
pp.addAll(pp2);
++gd;
}
if (p.full() && p.d < gd) {
p.put(k, v);
Page<K, V> p1, p2;
p1 = new Page<K, V>();
p2 = new Page<K, V>();
for (K k2 : p.m.keySet()) {
V v2 = p.m.get(k2);
int h = k2.hashCode() & ((1 << gd) - 1);
if ((h | (1 << p.d)) == h)
p2.put(k2, v2);
else
p1.put(k2, v2);
}
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < pp.size(); ++i)
if (pp.get(i) == p)
l.add(i);
for (int i : l)
if ((i | (1 << p.d)) == i)
pp.set(i, p2);
else
pp.set(i, p1);
p1.d = p.d + 1;
p2.d = p1.d;
} else
p.put(k, v);
}
public V get(K k) {
return getPage(k).get(k);
}
public static void main(String[] args) {
int N = 500000;
Random r = new Random();
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
l.add(i);
}
for (int i = 0; i < N; ++i) {
int j = r.nextInt(N);
int t = l.get(j);
l.set(j, l.get(i));
l.set(i, t);
}
EH2<Integer, Integer> eh = new EH2<Integer, Integer>();
for (int i = 0; i < N; ++i) {
eh.put(l.get(i), l.get(i));
}
for (int i = 0; i < N; ++i) {
System.out.printf("%d:%d , ", i, eh.get(i));
if (i % 10 == 0)
System.out.println();
}
}
}
A Java implementation of linear hashing[edit | edit source]
( usable for simple database indexing of arbitrary size, (almost ?) )
This code evolved out of a need for a bigger Java HashMap. Originally, a Java HashMap standard object was used as a Map to index a heap like database file ( DBF format). But then, a file was encountered with so many records that the OutOfMemoryError was being thrown, so linear hashing seemed like a reasonably simple algorithm to use as a disk based index scheme.
Initially, linear hashing was implemented behind the Java Map interface, mainly the put(k,v) and get(k,v) methods. Generics was used, in order not to get too involved in the key and value details.
debugging to achieve functionality[edit | edit source]
Custom dumps to System.err was used to verify that blocks were being created, filled, and overflow blocks were of expected number if they existed ( no. = 1 ). This was all done in a purely in-memory implementation.
Later, the standard Java decoupling was introduced, where the original LHMap2 class accepted listeners to events, such as when a block was needed. The listener was then implemented as a block file manager, loading blocks into the block list of the memory LHMap2 object whenever a null block was encountered on the block list, and checking whether virtual machine runtime free memory was low, and retiring blocks using just a basic first-to-last-listed cache removal algorithm (not least recently used (LRU), not least often used ) by saving them to disk file, and then actively invoking the system garbage collector.
Because an application use case existed, which was to externally index a large DBF table, this use case was used as the main test harness for the algorithm implementation.
package linearhashmap;
import java.io.Externalizable;
import java.io.IOException;
import java.io.ObjectInput;
import java.io.ObjectOutput;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.TreeMap;
import java.util.TreeSet;
/**
*
* @param <K>
* key type , must implement equals() and hashCode()
* @param <V>
* value type
*
*
*/
public class LHMap2<K, V> implements Map<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 3095071852466632996L;
/**
*
*/
public static interface BlockListener<K, V> {
public void blockRequested(int block, LHMap2<K, V> map);
}
List<BlockListener<K, V>> listeners = new ArrayList<BlockListener<K, V>>();
// int savedBlocks;
int N;
int level = 0;
int split = 0;
int blockSize;
long totalWrites = 0;
List<Block<K, V>> blockList = new ArrayList<Block<K, V>>();
public void addBlockListener(BlockListener<K, V> listener) {
listeners.add(listener);
}
void notifyBlockRequested(int block) {
for (BlockListener<K, V> l : listeners) {
l.blockRequested(block, this);
}
}
public LHMap2(int blockSize, int nStartingBlocks) {
this.blockSize = blockSize;
this.N = nStartingBlocks;
for (int i = 0; i < nStartingBlocks; ++i) {
addBlock();
}
Runtime.getRuntime().addShutdownHook(new Thread(new Runnable() {
@Override
public void run() {
showStructure();
}
}));
}
public static class Block<K, V> implements Externalizable {
/**
*
*/
int j = 0;
Block<K, V> overflow = null;
LinkedList<K> keyList = new LinkedList<K>();
LinkedList<V> valueList = new LinkedList<V>();
transient private LHMap2<K, V> owner;
transient private Map<K, V> shadow = new TreeMap<K, V>();
private boolean changed = false;
private int size = 0;
public LHMap2<K, V> getOwner() {
return owner;
}
public void setOwner(LHMap2<K, V> owner) {
this.owner = owner;
Block<K, V> ov = overflow;
while (ov != null) {
overflow.setOwner(owner);
ov = ov.overflow;
}
}
public Block() {
super();
}
public Block(LHMap2<K, V> map) {
setOwner(map);
}
public V put(K k, V v) {
setChanged(true);
V v2 = replace(k, v);
if (v2 == null) {
++size;
if (keyList.size() == getOwner().blockSize) {
if (overflow == null) {
getOwner().blockOverflowed(this, k, v);
} else {
overflow.put(k, v);
}
} else {
keyList.addFirst(k);
valueList.addFirst(v);
}
}
return v2;
}
void setChanged(boolean b) {
changed = b;
}
public Map<K, V> drainToMap(Map<K, V> map) {
while (!keyList.isEmpty()) {
K k = keyList.removeLast();
V v = valueList.removeLast();
map.put(k, v);
}
if (overflow != null)
map = overflow.drainToMap(map);
garbageCollectionOverflow();
return map;
}
public void updateMap(Map<K, V> map) {
Iterator<K> ik = keyList.descendingIterator();
Iterator<V> iv = valueList.descendingIterator();
while (ik.hasNext() && iv.hasNext()) {
map.put(ik.next(), iv.next());
}
if (overflow != null)
overflow.updateMap(map);
}
private void garbageCollectionOverflow() {
if (overflow != null) {
overflow.garbageCollectionOverflow();
overflow = null;
}
}
public void addOverflowBucket() {
// assert overflow is needed
if (keyList.size() < getOwner().blockSize)
return;
if (overflow == null) {
overflow = new Block<K, V>(getOwner());
} else {
overflow.addOverflowBucket();
}
}
public V replace(K key, V v2) {
if (overflow != null) {
V v = overflow.replace(key, v2);
if (v != null)
return v;
}
Iterator<K> i = keyList.listIterator();
int j = 0;
while (i.hasNext()) {
if (key.equals(i.next())) {
V v = valueList.get(j);
if (v2 != null) {
valueList.set(j, v2);
}
return v;
}
++j;
}
return null;
}
public boolean isChanged() {
return changed;
}
@Override
public void readExternal(ObjectInput arg0) throws IOException,
ClassNotFoundException {
int sz = arg0.readInt();
for (int i = 0; i < sz; ++i) {
K k = (K) arg0.readObject();
V v = (V) arg0.readObject();
shadow.put(k, v);
}
}
public void loadFromShadow(LHMap2<K, V> owner) {
setOwner(owner);
Block<K, V> b = this;
for (K k : shadow.keySet()) {
if (b.keyList.size() == owner.blockSize) {
Block<K, V> overflow = new Block<K, V>(owner);
b.overflow = overflow;
b = overflow;
}
b.keyList.add(k);
b.valueList.add(shadow.get(k));
}
shadow.clear();
}
@Override
public void writeExternal(ObjectOutput arg0) throws IOException {
if (!changed)
return;
Map<K, V> map = new TreeMap<K, V>();
updateMap(map);
int sz = map.size();
arg0.writeInt(sz);
for (K k : map.keySet()) {
arg0.writeObject(k);
arg0.writeObject(map.get(k));
}
setChanged(false);
}
}
void init() {
for (int i = 0; i < N; ++i) {
addBlock();
}
}
/**
* @param hashValue
* @return a bucket number.
*/
int getDynamicHash(int hashValue) {
long unsignedHash = ((long) hashValue << 32) >>> 32;
// ^^ this long cast needed
int h = (int) (unsignedHash % (N << level));
// System.err.println("h = " + h);
if (h < split) {
h = (int) (unsignedHash % (N << (level + 1)));
// System.err.println("h < split, new h = " + h);
}
return h;
}
@Override
public V put(K k, V v) {
++totalWrites;
int h = getDynamicHash(k.hashCode());
Block<K, V> b = getBlock(h);
b.put(k, v);
return v;
}
public long getTotalWrites() {
return totalWrites;
}
private Block<K, V> getBlock(int h) {
notifyBlockRequested(h);
return blockList.get(h);
}
void blockOverflowed(Block<K, V> b, K k, V v) {
splitNextBucket();
b.addOverflowBucket();
b.put(k, v);
}
private void splitNextBucket() {
Block<K, V> b = getBlock(split);
TreeMap<K, V> map = new TreeMap<K, V>();
b.drainToMap(map);
addBlock();
System.err.printf("split N LEVEL %d %d %d \n", split, N, level);
if (++split >= (N << level)) {
++level;
split = 0;
}
for (K k : map.keySet()) {
V v = map.get(k);
int h = getDynamicHash(k.hashCode());
System.err.println(h + " ");
Block<K, V> b2 = getBlock(h);
b2.put(k, v);
}
}
private Block<K, V> addBlock() {
Block<K, V> b = new Block<K, V>(this);
blockList.add(b);
return b;
}
@Override
public void clear() {
blockList = new ArrayList<Block<K, V>>();
split = 0;
level = 0;
totalWrites = 0;// savedBlocks = 0;
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return values().contains(value);
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
TreeSet<Map.Entry<K, V>> set = new TreeSet<Map.Entry<K, V>>();
Set<K> kk = keySet();
for (K k : kk) {
final K k2 = k;
set.add(new Entry<K, V>() {
@Override
public K getKey() {
return k2;
}
@Override
public V getValue() {
return get(k2);
}
@Override
public V setValue(V value) {
return put(k2, value);
}
});
}
return set;
}
@Override
public V get(Object key) {
int h = getDynamicHash(key.hashCode());
Block<K, V> b = getBlock(h);
return b.replace((K) key, null);
}
@Override
public boolean isEmpty() {
return size() == 0;
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
kk.addAll(b.keyList);
Block<K, V> ov = b.overflow;
while (ov != null) {
kk.addAll(ov.keyList);
ov = ov.overflow;
}
}
return kk;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public V remove(Object key) {
return null;
}
@Override
public int size() {
long sz = longSize();
return (int) (sz > Integer.MAX_VALUE ? Integer.MAX_VALUE
: sz);
}
public long longSize() {
long sz = 0;
for (Block<K, V> b : blockList) {
Block<K, V> b1 = b;
while (b1 != null) {
sz += b1.size;
b1 = b.overflow;
}
}
return sz;
}
@Override
public Collection<V> values() {
ArrayList<V> list = new ArrayList<V>();
Set<K> kk = keySet();
for (K k : kk) {
list.add(get(k));
}
return list;
}
private void showStructure() {
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
Block<K, V> ov = b.overflow;
int k = 0;
while (ov != null) {
ov = ov.overflow;
++k;
}
System.out.println("Block " + i + " size " + b.keyList.size()
+ " overflow blocks = " + k);
}
}
}
Each block is a file in this implementation, because blocks are variably sized here to account for generics and variable sized key and value pairs, and overflow blocks are conceptual, not actual as on disc storage, because the block's contents and that of its overflow bucket(s), are saved as a list of alternating keys and values in this implementation. Methods for saving and loading to Object streams was used in a standard java customized object persistence way by implementing the Externalizable interface in the Block data class.
package linearhashmap;
import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Random;
/**
* This class manages the LHMap2 class block disk swapping, and saves and load an instance of the LHMap2 class.
* It has been used to externally index a legacy file based database of 100,000 record master table, and 1,000,000 record
* sized child tables, and accounts for heap space available in the java virtual machine, so that OutOfMemory errors
* are avoided when the heap space is low by putting blocks back on files, and garbage collecting them.
* The main performance bottleneck appeared when loading a million record table for an index , on initial creation
* of the index.
* @author doctor
*
* @param <K>
* @param <V>
*/
public class LHMap2BlockFileManager<K, V> implements
LHMap2.BlockListener<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 2615265603397988894L;
LHMap2BlockFileManagerData data = new LHMap2BlockFileManagerData(
new byte[10000], new Random(), 0, new ArrayList<Integer>(), 0);
public LHMap2BlockFileManager(File baseDir, String name, int maxBlocks,
double unloadRatio) {
data.home = new File(baseDir, name);
if (!data.home.exists())
data.home.mkdir();
this.data.maxBlocks = maxBlocks;
this.data.unloadRatio = unloadRatio;
}
@Override
public void blockRequested(int block, LHMap2<K, V> map) {
LHMap2.Block<K, V> b = map.blockList.get(block);
if (b == null) {
int tries = 3;
File f = new File(data.home, Integer.toString(block));
do {
if (f.exists())
break;
if (!f.exists()) {
if (--tries >= 0)
fatal(block);
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
} while (true);
try {
ByteArrayInputStream bis = new ByteArrayInputStream(data.buf);
FileInputStream fis = new FileInputStream(f);
int sz = fis.read(data.buf);
fis.close();
addByteStats(sz);
ObjectInputStream ois = new ObjectInputStream(bis);
b = new LHMap2.Block<K, V>();
b.readExternal(ois);
ois.close();
b.loadFromShadow(map);
map.blockList.set(block, b);
--data.retired;
} catch (FileNotFoundException e) {
e.printStackTrace();
fatal(block);
} catch (IOException e) {
e.printStackTrace();
fatal(block);
} catch (ClassNotFoundException e) {
e.printStackTrace();
fatal(block);
}
}
int size = map.blockList.size();
try {
long freeMemory = Runtime.getRuntime().freeMemory();
long limitMemory = (long) (data.avgBlockSize * data.unloadRatio * size);
if (block % 30 == 0)
System.err.println("free memory =" + freeMemory + " limit "
+ limitMemory);
if (map.split % 20 == 19) {
// this is just to add statistics before really needing to retire
retireRandomBlock(map, block);
++data.retired;
} else if (freeMemory < limitMemory) {
for (int i = 0; i < size / 4; ++i) {
retireRandomBlock(map, block);
++data.retired;
}
System.runFinalization();
System.gc();
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
private void addByteStats(int sz) {
++data.avgCount;
data.avgBlockSize = (int) ((data.avgBlockSize
* (data.avgCount - 1) + sz) / data.avgCount);
}
public void retireRandomBlock(LHMap2<K, V> map, int notThisOne)
throws FileNotFoundException, IOException {
int pick = 0;
int size = map.blockList.size();
LHMap2.Block<K, V> b = null;
for (pick = 0; pick < size
&& (pick == notThisOne || (b = map.blockList.get(pick)) == null); ++pick)
;
if (pick < size)
retireOneBlock(map, pick, b);
}
private void retireOneBlock(LHMap2<K, V> map, int pick, LHMap2.Block<K, V> b)
throws IOException, FileNotFoundException {
if (b == null)
return;
if (b.isChanged()) {
// System.err.println("Retiring " + pick);
File f = new File(data.home, Integer.toString(pick));
ByteArrayOutputStream bos = new ByteArrayOutputStream();
ObjectOutputStream oos = new ObjectOutputStream(bos);
b.writeExternal(oos);
oos.flush();
oos.close();
FileOutputStream fos = new FileOutputStream(f);
byte[] bb = bos.toByteArray();
fos.write(bb);
fos.flush();
fos.close();
if (bb.length > data.buf.length) {
data.buf = bb;
}
}
map.blockList.set(pick, null);
b = null;
}
private void fatal(int block) {
Exception e = new Exception();
try {
throw e;
} catch (Exception e2) {
e2.printStackTrace();
}
System.err.println("block " + block
+ " requested and it is not in blocklist and not a file");
for (int i : data.retirees) {
System.err.print(i + " ");
}
System.err.println(" were retired");
System.exit(-2);
}
public static boolean metaExists(File indexDir, String name) {
File home = new File(indexDir, name);
return new File(home, "LinearMap2").exists();
}
public static <K, V> LHMap2<K, V> load(File baseDir, String name)
throws FileNotFoundException, IOException, ClassNotFoundException {
File home = new File(baseDir, name);
File f2 = new File(home, "LinearMap2");
ObjectInputStream ois = new ObjectInputStream(new FileInputStream(f2));
LHMap2<K, V> map = (LHMap2<K, V>) ois.readObject();
ois.close();
loadBlocks(map);
return map;
}
private static <K, V> void loadBlocks(LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(map);
int size = map.blockList.size();
for (int i = 0; i < size; ++i) {
mgr.blockRequested(i, map);
}
}
public static <K, V> LHMap2BlockFileManager<K, V> getBlockManagerListener(
LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = (LHMap2BlockFileManager<K, V>) map.listeners
.get(0);
return mgr;
}
public static void save(File indexDir, String name,
LHMap2<?, ?> offsetMap) throws FileNotFoundException, IOException {
retireAllBlocks(offsetMap);
File home = new File(indexDir, name);
File f2 = new File(home, "LinearMap2");
ObjectOutputStream oos = new ObjectOutputStream(
new FileOutputStream(f2));
oos.writeObject(offsetMap);
oos.close();
}
private static <K, V> void retireAllBlocks(LHMap2<K, V> offsetMap)
throws FileNotFoundException, IOException {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(offsetMap);
int sz = offsetMap.blockList.size();
for (int i = 0; i < sz; ++i) {
LHMap2.Block<K, V> b = offsetMap.blockList.get(i);
// offsetMap.blockList.set(i, null); // mark for reloading as block
// destroyed after writing
if (b != null) {
mgr.retireOneBlock(offsetMap, i, b);
}
}
}
}
package linearhashmap;
import java.io.File;
import java.io.Serializable;
import java.util.List;
import java.util.Random;
public class LHMap2BlockFileManagerData implements Serializable{
/**
*
*/
private static final long serialVersionUID = 1L;
public byte[] buf;
public Random r;
public File baseDir;
public File home;
public int maxBlocks;
public int retired;
public double unloadRatio;
public List<Integer> retirees;
public int avgBlockSize;
public long avgCount;
public LHMap2BlockFileManagerData(byte[] buf, Random r, int retired,
List<Integer> retirees, long avgCount) {
this.buf = buf;
this.r = r;
this.retired = retired;
this.retirees = retirees;
this.avgCount = avgCount;
}
}
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
References[edit | edit source]
- ↑ The simplest hash table schemes -- "open addressing with linear probing", "separate chaining with linked lists", etc. -- have O(n) lookup time in the worst case where (accidentally or maliciously) most keys "collide" -- most keys are hashed to one or a few buckets. Other hash table schemes -- "cuckoo hashing", "dynamic perfect hashing", etc. -- guarantee O(1) lookup time even in the worst case. When a new key is inserted, such schemes change their hash function whenever necessary to avoid collisions.
- ↑ Wikipedia: Comparison of programming languages (mapping) shows how many programming languages provide hash table functionality.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
Sets are helpful tools in a software application where, just as in mathematics, similar abstract objects are aggregated into collections. A mathematical set has a fairly simple interface and can be implemented in a surprising number of ways.
Set<item-type> ADT
contains(test-item:item-type):Boolean- True if test-item is contained in the Set.
insert(new-item:item-type)- Adds new-item into the set.
remove(item:item-type)- Removes item from the set. If item wasn't in the set, this method does nothing.
remove(item-iter:List Iterator<item-type>)- Removes the item referred to by item-iter from the set.
get-begin():List Iterator<item-type>- Allows iteration over the elements in the Set.
get-end():List Iterator<item-type>- Also allows iteration over the elements in the Set.
union(other:Set<item-type>):Set<item-type>- Returns a set containing all elements in either this or the other set. Has a default implementation.
intersect(other:Set<item-type>):Set<item-type>- Returns a set containing all elements in both this and the other set. Has a default implementation.
subtract(other:Set<item-type>):Set<item-type>- Returns a set containing all elements in this but not the other set. Has a default implementation.
is-empty():Boolean- True if no more items can be popped and there is no top item.
get-size():Integer- Returns the number of elements in the set.
All operations can be performed in time.
List implementation[edit | edit source]
There are several different ways to implement sets. The simplest, but in most cases least efficient, method is to simply create a linear list (an array, linked list or similar structure) containing each of the elements in the set. For the most basic operation, testing membership, a possible implementation could look like
function contains(List<T> list, T member)
for item in list
if item == member
return True
return False
To add new members to this set, simply add the element to beginning or end of the list. (If a check is done to ensure no duplicate elements, some other operations may be simpler.) Other operations can be similarly implemented in terms of simple list operations. Unfortunately, the membership test has a worst-case running time of if the item is not in the list, and even an average-case time of the same, assuming the item is equally likely to be anywhere in the list. If the set is small, or if frequently accessed items can be placed near the front of the list, this may be an efficient solution, but other options can have a faster running time.
Assuming elements can be ordered and insertions and deletions are rare, a list guaranteed to be in sorted order with no duplicate elements can be much more efficient. Using an ordered list, the membership test can be efficient to the order of . Additionally, union, intersection and subtraction can be implemented in linear time, whereas they would take quadratic time with unordered lists.
Bit array implementation[edit | edit source]
For certain data, it may be more practical to maintain a bit array describing the contents of the set. In this representation, there is a 1 or 0 corresponding to each element of the problem domain, specifying whether the object is an element of the set. For a simple case, assume that only integers from 0 to n can be members of the set, where n is known beforehand. This can be represented by a bit array of length n+1. The contains operation is simple:
function contains(BitArray array, Int member)
if member >= length(array)
return False
else if array[member] == 1
return True
else
return False
To add or remove an element from this sort of set, simply modify the bit array to reflect whether that index should be 1 or 0. The membership runs in exactly (constant) time, but it has a severely restricted domain. It is possible to shift the domain, going from m to n with step k, rather than 0 to n with step 1 as is specified above, but there is not much flexibility possible here. Nevertheless, for the right domain, this is often the most efficient solution.
Bit arrays are efficient structures for storing sets of Boolean variables. One example is a set of command line options that enable various run-time behavior for the application. C and similar languages offer bit-wise operators that let the programmer access a bit field in a single machine instruction, where array access would normally need two or three instructions including a memory read operation. A full-featured bit set implementation includes operators for computing a set union, set intersection, set difference, and element values.[1]
Associative array implementation[edit | edit source]
Associative arrays—that is, hash tables and binary search trees, represent a heavyweight but general representation of sets. Binary trees generally have time implementations for lookup and mutation for a particular key, and hash tables have a implementation (though there is a higher constant factor). Additionally, they are capable of storing nearly any key type. The membership test is trivial: simply test if the potential set member exists as a key in the associative array. To add an element, just add the set member as a key in the associative array, with a dummy value. In optimized implementations, instead of reusing an existing associative array implementation, it is possible to write a specialized hash table or binary tree which does not store values corresponding to keys. Values are not meaningful here, and they take up a constant factor of additional memory space.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
References[edit | edit source]
- ↑ Samuel Harbison and Guy Steele. C: a reference manual. 2002.
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
It is important to fully understand the problem you need to solve before choosing a data structure because each structure is optimized for a particular job. Hash tables, for example, favor fast lookup times over memory usage while arrays are compact and inflexible. Other structures, such as stacks, are optimized to enforce rigid rules on how data is added, removed and accessed throughout the program execution. A good understanding of data structures is fundamental because it gives us the tools for thinking about a program's behavior in a structured way.
[TODO:] Use asymptotic behaviour to decide, most importantly seeing how the structure will be used: an infrequent operation does not need to be fast if it means everything else will be much faster
[TODO:] Can use a table like this one to compare the asymptotic behaviour of every structure for every operation on it.
| Array | Dynamic Array | Array Deque | Singly Linked List | Double Linked List | |
|---|---|---|---|---|---|
| Push (Front) | - | O(n) | O(1) | O(1) | O(1) |
| Pop (Front) | - | O(n) | O(1) | O(1) | O(1) |
| Push (Back) | - | O(1) | O(1) | O(n), maybe O(1)* | O(1) |
| Pop (Back) | - | O(1) | O(1) | O(n) | O(1) |
| Insert before (given iterator) | - | O(n) | O(n) | O(n) | O(1) |
| Delete (given iterator) | O(n) | O(n) | O(n) | O(1) | |
| Insert after (given iterator) | O(n) | O(n) | O(1) | O(1) | |
| Delete after (given iterator) | - | O(n) | O(n) | O(1) | O(1) |
| Get nth element (random access) | O(1) | O(1) | O(1) | O(n) | O(n) |
| Good for implementing stacks | no | yes (back is top) | yes | yes (front is top) | yes |
| Good for implementing queues | no | no | yes | maybe* | yes |
| C++ STL | std::array
|
std::vector
|
std::deque
|
std::forward_list
|
std::list
|
| Java Collections | java.util.Array
|
java.util.ArrayList
|
java.util.ArrayDeque
|
- | java.util.LinkedList
|
* singly-linked lists can push to the back in O(1) with the modification that you keep a pointer to the last node
| Sorted Array | Sorted Linked List | Self-balancing Binary Search Tree | Hash Table | |
|---|---|---|---|---|
| Find key | O(log n) | O(n) | O(log n) | O(1) average O(n) worst |
| Insert element | O(n) | O(n) | O(log n) | O(1) average O(n) worst |
| Erase key | O(n) | O(n) | O(log n) | O(1) average O(n) worst |
| Erase element (given iterator) | O(n) | O(1) | O(1) | O(1) |
| Can traverse in sorted order? | yes | yes | yes | no |
| Needs | comparison function | comparison function | comparison function | hash function |
| C++ STL | - | - | std::setstd::mapstd::multiset
|
std::unordered_setstd::unordered_mapstd::unordered_multiset
|
| Java Collections | - | - | java.util.TreeSet
|
java.util.HashSet
|
- Please correct any errors
| Binary Search | AVL Tree | Binary Heap (min) | Binomial Queue (min) | |
|---|---|---|---|---|
| Insert element | O(log n) | O(log n) | O(log n) | O(1) (on average) |
| Erase element | O(log n) | O(log n) | unavailable | unavailable |
| Delete min element | O(log n) | O(log n) | O(log n) | O(log n) |
| Find min element | O(log n) | O(log n) | O(1) | O(log n) (can be O(1) if ptr to smallest) |
| Increase key | unavailable | unavailable | O(log n) | O(log n) |
| Decrease key | unavailable | unavailable | O(log n) | O(log n) |
| Find | O(log n) | O(log n) | unavailable | unavailable |
| Delete element | O(log n) | O(log n) | unavailable | unavailable |
| Create | O(1) | O(1) | O(1) | O(1) |
| find kth smallest | O(log n) | O(log n) | O((k-1)*log n) | O(k*log n) |
| Hash table (hash map) | |
|---|---|
| Set Value | Ω(1), O(n) |
| Get Value | Ω(1), O(n) |
| Remove | Ω(1), O(n) |
[TODO:] Can also add a table that specifies the best structure for some specific need e.g. For queues, double linked. For stacks, single linked. For sets, hash tables. etc...
[TODO:] Could also contain table with space complexity information (there is a significative cost in using hashtables or lists implemented via arrays, for example).
Data Structures
Introduction -
Asymptotic Notation -
Arrays -
List Structures & Iterators
Stacks & Queues -
Trees -
Min & Max Heaps -
Graphs
Hash Tables -
Sets -
Tradeoffs
























































































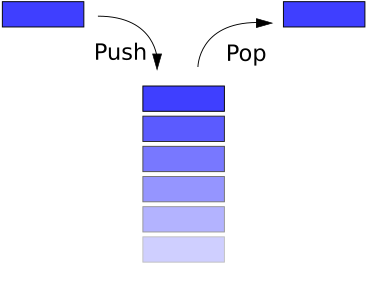















![{\displaystyle array[floor(N/2)]>array[N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24c556c36e19d6cdca1424cc3846013f01027bb6)










![{\displaystyle \left(i,\left[1..n\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/536da7d1241489aca63f932e0a87674ef50aa9ed)


