Data Management in Bioinformatics/ER Theory
| Chapter Navigation | |
| Top | E/R Theory - Normalization - Data Querying - Integrating SQL and Programming Languages |
Theory of Relations[edit | edit source]
Introduction to Biological Databases[edit | edit source]
Organisms are categorized as Prokaryotes and Eukaryotes. The central dogma of molecular biology lays down that DNA is transcribed to mRNA, which is then translated to proteins. The proteins carry out life functions in the cell.
The genetic material in a cell consists of several strands of DNA double helix formed into a super coiled structure. The DNA molecule consists of sugar-phosphate backbone on which nucleotides form base pairs. The 4 bases are denoted by the letters A,C,T and G. T pairs with A and C pairs with G in the DNA double helix.
A few sample Biological Databases[edit | edit source]
- Genomes
- GenBank: a collection of all publicly available DNA sequences maintained by NIH.[1]
- Protein
- PDB: A protein database [2]
- Function & Annotation
- Interaction Databases - Protein-protein Interaction
- BIND: Biomolecular Interaction Network Database [3]
- Pathways
- Chemical Reaction Pathways: KEGG Kyoto Encyclopedia of Genes and Genomes
- Signal Transduction (i.e. response to external signals): STKE Signal Transduction Knowledge Environment [4]
- Text
- PubMed:Collection of biology research articles. [5]
- Organism Specific database
The Jan Issue of Nucleic Acids Research journal is a catalog of biological databases.
Course content[edit | edit source]
- Data Models
- Relational
- Object Oriented
- Hierarchical
- Semi-structured
- Unstructured (e.g. Text)
- Model of Querying: SQL
- Information Integration
- Data Mining
The Relational Model[edit | edit source]
- Set
- A collection of objects
- Let and be two sets, and
- Cartesian Product
- of is the set consisting all possible pairs taking one object from set and the other from set .
- A × B = {(a,1),(a,2),(a,4),(b,1),(b,2),(b,4),(c,1),(c,2),(c,4)}
- Relation
- is a subset of the Cartesian product.
An example of a relation[edit | edit source]
| Gene ID | Name | Annotation | Expt ID | Expt. Desc. | Expression Level |
|---|---|---|---|---|---|
| g2347 | p53 | Tumor Suppressor | e0 | Heat Shock | +2 |
| g2347 | p53 | Tumor Suppressor | e1 | Cold Shock | -1 |
| g2347 | p53 | Tumor Suppressor | e2 | Desiccation | 0 |
| ... | ... | ... | ... | ... | ... |
The above is an example of an Un-Normalized Relation. And has the following problems:
- Redundancy: The gene information is repeated for different experiments and potentially experiment information can be common to several genes
- Update Anomaly: If the annotation of a gene needs to be updated, several rows of the table need update.
- Deletion Anomaly: Deleting a gene can result in loss of information about an experiment.
Designing Tables[edit | edit source]
Entity-Relationship Diagrams[edit | edit source]
The above figure suggests how the E/R model is used in database design. We start with ideas about the information we want to model and render them in the E/R model. The abstract E/R design is then converted to a schema in the data-specification language of some DBMS. Most commonly, this DBMS uses the relational model. If so, then by a fairly mechanical process, the abstract design is converted to a concrete, relational design, called a "relational database schema".
| Entity (Nouns) | Relation (Verbs) |
|---|---|
| Gene | Subjected To |
| Experiment |
Reading a 2-way relationship[edit | edit source]

Many-to-many relation (no arrows)
- One A can be related to many B's e.g one gene can be subjected to many experiments
- One B can be related to many A's e.g. one experiment can subject many genes

One-to-one (arrows in both sides)
- One A can be related at most one B e.g. one DNA molecule can be transcribed to at most one RNA primary transcript
- One B can be related at most one A e.g. one RNA primary transcript can be transcribed from at most one DNA molecule

many-to-one (an arrow to the one side)
- One A can be related to at most one B e.g. one codon can encode at most one amino acid
- One B can be related to many A's e.g. one amino acid can be encoded by many codons
A 3-way relationship[edit | edit source]

S => Student, C => Course, I => Instructor
- Any (S,C) pair can have many I's
- Any (S,I) pair can have many C's
- Any (C,I) pair can have many S's
Replacing a 3-way relationship[edit | edit source]
The following is another example of the 3-way relationship (ternary relationship)
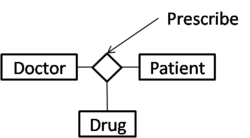
The relationship can be replaced with a set of binary relationships as in the following:
For instance,
A = > Doctor, B => Patient, C => Drug, R => Prescribe
| R | A | B | C |
|---|---|---|---|
| r1 | a1 | b1 | c2 |
| r2 | a1 | b2 | c1 |
| r3 | a2 | b1 | c1 |
| r4 | a2 | b1 | c2 |
However, the diagram is not equivalent to the following diagram:

The 2=way relations in the diagram are (A,B), (B,C), and (C,A). The three binary relations have different meaning with the given ternary relation. For example, association of a set of doctors with a certain pair of a patient and a drug cannot be modeled with the binary relationships.
It is modeling decision whether a relation should be represented as a ternary relation or a set binary relations such as the above.
Boxing a 2-way relationship[edit | edit source]
Usually, boxing a thing means that the entity is important to have its own space rather than a concept to model relationships. When boxing a relation, the name of the entity often becomes the noun phrases from the verb in the relation name.
For example, the ER model such as the following

An examples of tables for the model is:
| Birth | Mother | Baby |
|---|---|---|
| b1 | Sue | Tom |
| b2 | Sue | Marry |
| b3 | Jane | Robert |
The following model also can be used to replace the original model. But it has different meaning with the previous model. An example of tables for the model is:
| Birth | Mother | Baby |
|---|---|---|
| b1 | Sue | Tom |
| b1 | Sue | Marry |
| b2 | Jane | Robert |
Such a boxing of an relationship give more flexibility.
Attributes, Keys[edit | edit source]
The properties of a entity or a relation is called as attributes. The attributes are denoted as balloons attached to the entity or the relation. The attributes are also required to be in table as columns.
Gene expression process can be divided into several steps and transcription process is one of the steps. mRNA is synthesized from DNA through the transcription process. Also, cDNA is synthesized from the mRNA through reverse transcription process. A microarray is a chip that a lot of DNA sequences are aligned on its surface. In DNA microarray experiment, the synthesized cDNA is poured on the chip and the cDNA binds to complementing DNA sequence on the chip by hybridization. The bound cDNA is measured to quantify the gene expression level in the experiment.
As mentioned before, a relation also can have attributes.
Here is an example of relations with attributes.

An attribute or a set of attributes whose value is unique for each instance of entity is called a candidate key. There can be multiple candidate keys for an entity and the candidate key selected to identify the entity is called a (primary) key. The name of the key is underlined in ER digram. For example, ssn and sid is unique for all students so both are candidate keys. either ssn or sid can be selected as the primary key for entity type 'student'.
Creating tables from ERD[edit | edit source]
Converting an E/R design to a relational database schema is fairly mechanical and straightforward
- Turn each entity set into a relation with the same set of attributes, and
- Replace a relationship by a relation whose attributes are the keys for the connected entity sets
For
- many-many relation - the key for the relation representing relationship must be the union of keys from the participating entity sets
- many-one relation - the key for the relation representing relationship must come from the many part
- one-one relation - key for either of the participating entity set could be a key for the relation
For example,

The key of 'takes' depend on the cardinality of the relation. The key for each cardinality of the relation is:
- many to many relation -> a,c
- one to many relation -> c
- one to one relation -> a or c
If 'takes' is an one to many cardinality relation, the tables generated from the model would be
Here are examples of generated tables for 3-way relations. Tables for A,B, and C is omitted.



either one of the following two tables is possible.
The following is an example for an unary relation.
Here is another example.

Weak sets[edit | edit source]
There can be many counties with the same name in different states. For example, counties with the name of Montgomery are in Virginia, Texas, Maryland, so on. So the name of a county cannot be the key for the entity of counties. However, a key for counties can be acquired by combining the name of states and the name of the county. Such entities that do not have key in their attributes are called weak sets or weak entities. The keys of such entities can be acquired from attributes of certain related entities. The related entities are often called identifying entities. The relation from the weak set to its identifying entities are called identifying relations.

The above ER diagram models shows a binary relation between States and Counties. The double bordered rectangle denotes the weak set and the identifying entity is States because combination of two characters for a state and the name of a county identify a county. The notation of double bordered relation in the diagram denotes the identifying relation too. The identifying entities can be found by searching the double bordered diamonds and see the arrow from the diamonds.

Weak sets are entity sets that don't supply all of their own keys (see diagram) They rely on other entity sets to supply some or all of their keys. We encode this E/R diagram as:
Notice that does not have written twice. We do not need to encode the weak relationship completely. It is implicit from the encoding of .

We encode the entity sets of this next E/R diagram as:
Questions about weak sets[edit | edit source]

No, it is not valid. For any instance of , there must only be one , otherwise it would have multiple instances of the same kind of key. There should be an arrow pointing to .

No, it is not valid. This diagram means:
- For every , , there is one
- For every , , there are many s
- For every , , there is one }
This does not exclude the possibility of one having many s. There is no unambiguous way to draw a weak set that draws keys from two other entity sets with an E/R diagram without having two separate relationships.
Causes of weak sets[edit | edit source]

- Converting a relationship to an entity set (see diagram)
- Hierarchy
Notice in #1 that there are arrows pointing to all the original entity sets. We need these, because each relation entity may only have one , , and .
Hierarchy is an interesting situation, which leads us into inheritance.
Inheritance[edit | edit source]
In this section, we will discuss inheritance; what it is, why we use it, and how to use it.
What is inheritance?[edit | edit source]
Inheritance occurs when one thing (an entity set) is a subset of something else (some other entity set).
One way to start examining if an entity set inherits from another entity set is to ask if " IS A ".
Inheritance is when you can say `$A$ IS A $B$' with a straight face, and if you ever run for office no one will point out that you said it. ~Naren Ramakrishnan
Are the following valid inheritance?
- apple IS A fruit
- apple IS A cow
- g23 IS A gene
- 1 is correct, because an apple is a fruit. #2 is not correct, because an apple is not a cow. #3, however, is not correct because g23 is a specific gene, it does not quite demonstrate what we want to see in inheritance. A better way to test for inheritance is if you can say "$A$ IS A TYPE OF $B$".
Why do we use inheritance?[edit | edit source]
We use inheritance to give subsets of entity sets the attributes of its parent entity set, and let it extend that with extra information. When we say that "$A$ IS A $B$", we are already communicating a lot of information. For example, when we say that an "apple IS A fruit", even if we don't quite know what an "apple" is, we've communicated that an "apple" has seeds, is a part of a larger plant, and tastes better than a typical vegetable.

Examine the diagram. A mammal is an animal, and so is a reptile. Both have an id, genus, weight, species, and safety level (whatever that means). Both mammals and reptiles inherit these attributes. It's important to note that in an inheritance relationship, the child entity set inherits the key of the parent entity set. In this example, the key for both mammals and reptiles is their animal id.
The reason why we bother creating separate entity sets for mammals and reptiles is that we want to add attributes to each. Notice that mammals have a hair count and reptiles have an egg count. Instead of creating an entirely new entity set to explain this, we simply use inheritance to say that a mammal is an animal that has a hair count, and a reptile is an animal that has an egg count. Some animals have both a hair count, and an egg count. Let's call these animals ``weirdos. We can see from the diagram, that we do not have to add any extra attributes to weirdos if we just use multiple inheritance and make a weirdo both a mammal and a reptile. Implicitly, a weirdo is also an animal and has all the attributes of an animal, including the key, id. In other words, inheritance is transitive.
How do we use inheritance?[edit | edit source]
We encode the entity sets in the diagram as:
We don't have to encode weirdos, they are implicit. Notice that while weak sets have different keys, inheriting sets don't have different keys. Notice also that inheriting sets get all of their parents' attributes, not just some of them.
Questions about inheritance[edit | edit source]

Yes, it could be valid, depending on the relationships. Consider the relationship between rural counties and states as "sells to". Also, notice that because we have single inheritance, we have to add an attribute to rural counties.

Yes, it could be valid. Consider the new relationship to also be "sells to".



























