Cognitive Psychology and Cognitive Neuroscience/Problem Solving from an Evolutionary Perspective
| Previous Chapter | Overview | Next Chapter |
Introduction[edit | edit source]
Same place, different day. Knut is sitting at his desk again, staring at a blank paper in front of him, while nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: "I need a plan!"
That thing Knut is confronted with is something everyone of us encounters in his daily life. He has got a problem – and he does not really know how to solve it. But what exactly is a problem? Are there strategies to solve problems? These are just a few of the questions we want to answer in this chapter.
We begin our chapter by giving a short description of what psychologists regard as a problem. Afterwards we are going to present different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts do solve problems and finally we will have a closer look at two topics: The neurophysiological background on the one hand and the question what kind of role can be assigned to evolution regarding problem solving on the other.
The most basic definition is “A problem is any given situation that differs from a desired goal”. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, learning, repeating and varying all kinds of complex movements, and so on. Though all these problems were of crucial importance during the evolutionary process that created us the way we are, they are by no means solved exclusively by humans. We find a most amazing variety of different solutions for these problems in nature (just consider, e.g., by which means a bat hunts its prey, compared to a spider). For this essay we will mainly focus on those problems that are not solved by animals or evolution, that is, all kinds of abstract problems (e.g. playing chess). Furthermore, we will not consider those situations as problems that have an obvious solution: Imagine Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognising the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. Still we will find that often the strategies we use to solve these problems are applicable to more basic problems, too.
Non-trivial, abstract problems can be divided into two groups:
Well-defined Problems[edit | edit source]
For many abstract problems it is possible to find an algorithmic solution. We call all those problems well-defined that can be properly formalised, which comes along with the following properties:
- The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later).
- There is a finite set of operators, that is, of rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.
- Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.
Not surprisingly, a problem that fulfils these requirements can be implemented algorithmically (also see convergent thinking). Therefore many well-defined problems can be very effectively solved by computers, like playing chess.
Ill-defined Problems[edit | edit source]
Though many problems can be properly formalised (sometimes only if we accept an enormous complexity) there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity, and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state: Formalising a problem of the kind “Please paint a beautiful picture” may be impossible. Still this is a problem most people would be able to access in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.
Nevertheless ill-defined problems often involve sub-problems that can be totally well-defined. On the other hand, many every-day problems that seem to be completely well-defined involve- when examined in detail- a big deal of creativity and ambiguities.
If we think of Knut's fairly ill-defined task of writing an essay, he will not be able to complete this task without first understanding the text he has to write about. This step is the first subgoal Knut has to solve. Interestingly, ill-defined problems often involve subproblems that are well-defined.
Restructuring – The Gestalt Approach[edit | edit source]
One dominant approach to Problem Solving originated from Gestalt psychologists in the 1920s. Their understanding of problem solving emphasises behaviour in situations requiring relatively novel means of attaining goals and suggests that problem solving involves a process called restructuring. Since this indicates a perceptual approach, two main questions have to be considered:
- How is a problem represented in a person's mind?
- How does solving this problem involve a reorganisation or restructuring of this representation?
This is what we are going to do in the following part of this section.
How is a problem represented in the mind?[edit | edit source]
In current research internal and external representations are distinguished: The first kind is regarded as the knowledge and structure of memory, while the latter type is defined as the knowledge and structure of the environment, such like physical objects or symbols whose information can be picked up and processed by the perceptual system autonomously. On the contrary the information in internal representations has to be retrieved by cognitive processes.
Generally speaking, problem representations are models of the situation as experienced by the agent. Representing a problem means to analyse it and split it into separate components:
- objects, predicates
- state space
- operators
- selection criteria
Therefore the efficiency of Problem Solving depends on the underlying representations in a person’s mind, which usually also involves personal aspects. Analysing the problem domain according to different dimensions, i.e., changing from one representation to another, results in arriving at a new understanding of a problem. This is basically what is described as restructuring. The following example illustrates this:
- Two boys of different age are playing badminton. The older one is a more skilled player, and therefore it is predictable for the outcome of usual matches who will be the winner. After some time and several defeats the younger boy finally loses interest in playing, and the older boy faces a problem, namely that he has no one to play with anymore.
- The usual options, according to M. Wertheimer (1945/82), at this point of the story range from 'offering candy' and 'playing another game' to 'not playing to full ability' and 'shaming the younger boy into playing'. All those strategies aim at making the younger stay.
- And this is what the older boy comes up with: He proposes that they should try to keep the bird in play as long as possible. Thus they change from a game of competition to one of cooperation. They'd start with easy shots and make them harder as their success increases, counting the number of consecutive hits. The proposal is happily accepted and the game is on again.
The key in this story is that the older boy restructured the problem and found out that he used an attitude towards the younger which made it difficult to keep him playing. With the new type of game the problem is solved: the older is not bored, the younger not frustrated.
Possibly, new representations can make a problem more difficult or much easier to solve. To the latter case insight– the sudden realisation of a problem’s solution – seems to be related.
Insight[edit | edit source]
There are two very different ways of approaching a goal-oriented situation. In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking.
The second way requires something new and different to achieve the goal, prior learning is of little help here. Such productive thinking is (sometimes) argued to involve insight. Gestalt psychologists even state that insight problems are a separate category of problems in their own right.
Tasks that might involve insight usually have certain features – they require something new and non-obvious to be done and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called "AHA-experience" – the solution pops up all of a sudden. At one time you do not have any ideas of the answer to the problem, you do not even feel to make any progress trying out different ideas, but in the next second the problem is solved.
For all those readers who would like to experience such an effect, here is an example for an Insight Problem: Knut is given four pieces of a chain; each made up of three links. The task is to link it all up to a closed loop and he has only 15 cents. To open a link costs 2, to close a link costs 3 cents. What should Knut do?

To show that solving insight problems involves restructuring, psychologists created a number of problems that were more difficult to solve for participants provided with previous experiences, since it was harder for them to change the representation of the given situation (see Fixation). Sometimes given hints may lead to the insight required to solve the problem. And this is also true for involuntarily given ones. For instance it might help you to solve a memory game if someone accidentally drops a card on the floor and you look at the other side. Although such help is not obviously a hint, the effect does not differ from that of intended help.
For non-insight problems the opposite is the case. Solving arithmetical problems, for instance, requires schemas, through which one can get to the solution step by step.
Fixation[edit | edit source]
Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation.
Functional fixedness[edit | edit source]
Functional fixedness concerns the solution of object-use problems. The basic idea is that when the usual way of using an object is emphasised, it will be far more difficult for a person to use that object in a novel manner. An example for this effect is the candle problem: Imagine you are given a box of matches, some candles and tacks. On the wall of the room there is a cork-board. Your task is to fix the candle to the cork-board in such a way that no wax will drop on the floor when the candle is lit. – Got an idea?
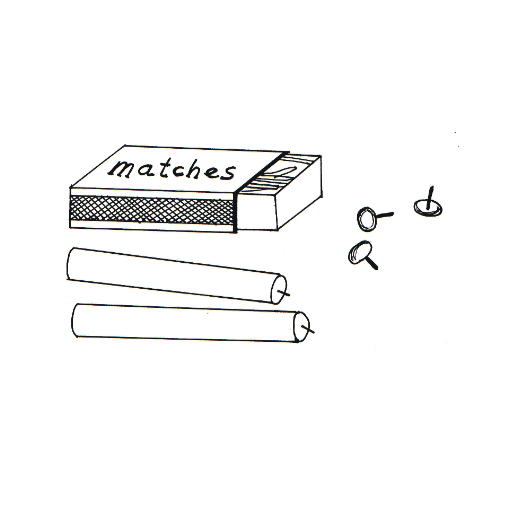
- Explanation: The clue is just the following: when people are confronted with a problem and given certain objects to solve it, it is difficult for them to figure out that they could use them in a different (not so familiar or obvious) way. In this example the box has to be recognised as a support rather than as a container.
A further example is the two-string problem: Knut is left in a room with a chair and a pair of pliers given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?

- Solution: Knut has to recognise he can use the pliers in a novel function – as weight for a pendulum. He can bind them to one of the :strings, push it away, hold the other string and just wait for the first one moving towards him. If necessary, Knut can even climb on the chair, but he is not that small, we suppose . . .
Mental fixedness[edit | edit source]
Functional fixedness as involved in the examples above illustrates a mental set – a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulties to vary the way of use (pliers as pendulum's weight).
One approach to studying fixation was to study wrong-answer verbal insight problems. It was shown that people tend to give rather an incorrect answer when failing to solve a problem than to give no answer at all.
- A typical example: People are told that on a lake the area covered by water lilies doubles every 24 hours and that it takes 60 days to cover the whole lake. Then they are asked how many days it takes to cover half the lake. The typical response is '30 days' (whereas 59 days is correct).
These wrong solutions are due to an inaccurate interpretation, hence representation, of the problem. This can happen because of sloppiness (a quick shallow reading of the problem and/or weak monitoring of their efforts made to come to a solution). In this case error feedback should help people to reconsider the problem features, note the inadequacy of their first answer, and find the correct solution. If, however, people are truly fixated on their incorrect representation, being told the answer is wrong does not help. In a study made by P.I. Dallop and R.L. Dominowski in 1992 these two possibilities were contrasted. In approximately one third of the cases error feedback led to right answers, so only approximately one third of the wrong answers were due to inadequate monitoring.[1]
Another approach is the study of examples with and without a preceding analogous task. In cases such like the water-jug task analogous thinking indeed leads to a correct solution, but to take a different way might make the case much simpler:
- Imagine Knut again, this time he is given three jugs with different capacities and is asked to measure the required amount of water. :Of course he is not allowed to use anything despite the jugs and as much water as he likes. In the first case the sizes are: 127 litres, 21 litres and 3 litres while 100 litres are desired.
- In the second case Knut is asked to measure 18 litres from jugs of 39, 15 and three litres size.
In fact participants faced with the 100 litre task first choose a complicate way in order to solve the second one. Others on the contrary who did not know about that complex task solved the 18 litre case by just adding three litres to 15.
Problem Solving as a Search Problem[edit | edit source]
The idea of regarding problem solving as a search problem originated from Alan Newell and Herbert Simon while trying to design computer programs which could solve certain problems. This led them to develop a program called General Problem Solver which was able to solve any well-defined problem by creating heuristics on the basis of the user's input. This input consisted of objects and operations that could be done on them.
As we already know, every problem is composed of an initial state, intermediate states and a goal state (also: desired or final state), while the initial and goal states characterise the situations before and after solving the problem. The intermediate states describe any possible situation between initial and goal state. The set of operators builds up the transitions between the states. A solution is defined as the sequence of operators which leads from the initial state across intermediate states to the goal state.
The simplest method to solve a problem, defined in these terms, is to search for a solution by just trying one possibility after another (also called trial and error).
As already mentioned above, an organised search, following a specific strategy, might not be helpful for finding a solution to some ill-defined problem, since it is impossible to formalise such problems in a way that a search algorithm can find a solution.
As an example we could just take Knut and his essay: he has to find out about his own opinion and formulate it and he has to make sure he understands the sources texts. But there are no predefined operators he can use, there is no panacea how to get to an opinion and even not how to write it down.
Means-End Analysis[edit | edit source]
In Means-End Analysis you try to reduce the difference between initial state and goal state by creating subgoals until a subgoal can be reached directly (probably you know several examples of recursion which works on the basis of this).
An example for a problem that can be solved by Means-End Analysis are the „Towers of Hanoi“:
Towers of Hanoi – A well defined problem
The initial state of this problem is described by the different sized discs being stacked in order of size on the first of three pegs (the “start-peg“). The goal state is described by these discs being stacked on the third pegs (the “end-peg“) in exactly the same order.

There are three operators:
- You are allowed to move one single disc from one peg to another one
- You are only able to move a disc if it is on top of one stack
- A disc cannot be put onto a smaller one.
In order to use Means-End Analysis we have to create subgoals. One possible way of doing this is described in the picture:
1. Moving the discs lying on the biggest one onto the second peg.
2. Shifting the biggest disc to the third peg.
3. Moving the other ones onto the third peg, too
You can apply this strategy again and again in order to reduce the problem to the case where you only have to move a single disc – which is then something you are allowed to do.
Strategies of this kind can easily be formulated for a computer; the respective algorithm for the Towers of Hanoi would look like this:
1. move n-1 discs from A to B
2. move disc #n from A to C
3. move n-1 discs from B to C
where n is the total number of discs, A is the first peg, B the second, C the third one. Now the problem is reduced by one with each recursive loop.
Means-end analysis is important to solve everyday-problems – like getting the right train connection: You have to figure out where you catch the first train and where you want to arrive, first of all. Then you have to look for possible changes just in case you do not get a direct connection. Third, you have to figure out what are the best times of departure and arrival, on which platforms you leave and arrive and make it all fit together.
Analogies[edit | edit source]
Analogies describe similar structures and interconnect them to clarify and explain certain relations. In a recent study, for example, a song that got stuck in your head is compared to an itching of the brain that can only be scratched by repeating the song over and over again.
Restructuring by Using Analogies[edit | edit source]
One special kind of restructuring, the way already mentioned during the discussion of the Gestalt approach, is analogical problem solving. Here, to find a solution to one problem – the so called target problem, an analogous solution to another problem – the source problem, is presented.
An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:
As a doctor you have to treat a patient with a malignant, inoperable tumour, buried deep inside the body. There exists a special kind of ray, which is perfectly harmless at a low intensity, but at the sufficient high intensity is able to destroy the tumour – as well as the healthy tissue on his way to it. What can be done to avoid the latter?
When this question was asked to participants in an experiment, most of them couldn't come up with the appropriate answer to the problem. Then they were told a story that went something like this:
A General wanted to capture his enemy's fortress. He gathered a large army to launch a full-scale direct attack, but then learned, that all the roads leading directly towards the fortress were blocked by mines. These roadblocks were designed in such a way, that it was possible for small groups of the fortress-owner's men to pass them safely, but every large group of men would initially set them off. Now the General figured out the following plan: He divided his troops into several smaller groups and made each of them march down a different road, timed in such a way, that the entire army would reunite exactly when reaching the fortress and could hit with full strength.
Here, the story about the General is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumour and the big army corresponds to the highly intensive ray. Consequently a small group of soldiers represents a ray at low intensity. The solution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumour from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumour itself gets destroyed by the ray at its full intensity.
M. Gick and K. Holyoak presented Duncker's radiation problem to a group of participants in 1980 and 1983. Only 10 percent of them were able to solve the problem right away, 30 percent could solve it when they read the story of the general before. After given an additional hint – to use the story as help – 75 percent of them solved the problem.
With this results, Gick and Holyoak concluded, that analogical problem solving depends on three steps:
1. Noticing that an analogical connection exists between the source and the target problem.
2. Mapping corresponding parts of the two problems onto each other (fortress → tumour, army → ray, etc.)
3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions → sending several weaker rays from different directions)
Next, Gick and Holyoak started looking for factors that could be helpful for the noticing and the mapping parts, for example:
Discovering the basic linking concept behind the source and the target problem.
-->picture coming soon<--
Schema[edit | edit source]
The concept that links the target problem with the analogy (the “source problem“) is called problem schema. Gick and Holyoak obtained the activation of a schema on their participants by giving them two stories and asking them to compare and summarise them. This activation of problem schemata is called “schema induction“.
The two presented texts were picked out of six stories which describe analogical problems and their solution. One of these stories was "The General" (remember example in Chapter 4.1).
After solving the task the participants were asked to solve the radiation problem (see chapter 4.2). The experiment showed that in order to solve the target problem reading of two stories with analogical problems is more helpful than reading only one story: After reading two stories 52% of the participants were able to solve the radiation problem (As told in chapter 4.2 only 30% were able to solve it after reading only one story, namely: “The General“).
Gick and Holyoak found out that the quality of the schema a participant developed differs. They classified them into three groups:
- Good schemata: In good schemata it was recognised that the same concept was used in order to solve the problem (21% of the participants created a good schema and 91% of them were able to solve the radiation problem).
- Intermediate schemata: The creator of an intermediate schema has figured out that the root of the matter equals (here: many small forces solved the problem). (20% created one, 40% of them had the right solution).
- Poor schemata: The poor schemata were hardly related to the target problem. In many poor schemata the participant only detected that the hero of the story was rewarded for his efforts (59% created one, 30% of them had the right solution).
The process of using a schema or analogy, i.e. applying it to a novel situation is called transduction. One can use a common strategy to solve problems of a new kind.
To create a good schema and finally get to a solution is a problem-solving skill that requires practise and some background knowledge.
How do Experts Solve Problems?[edit | edit source]
With the term expert we describe someone who devotes large amounts of his or her time and energy to one specific field of interest in which he, subsequently, reaches a certain level of mastery. It should not be of surprise that experts tend to be better in solving problems in their field than novices (people who are beginners or not as well trained in a field as experts) are. They are faster in coming up with solutions and have a higher success rate of right solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:
- Experts know more about their field,
- their knowledge is organised differently, and
- they spend more time analysing the problem.
When it comes to problems that are situated outside the experts' field, their performance often does not differ from that of novices.
Knowledge: An experiment by Chase and Simon (1973a, b) dealt with the question how well experts and novices are able to reproduce positions of chess pieces on chessboards when these are presented to them only briefly. The results showed that experts were far better in reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognise familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not pure size of knowledge that makes an expert more successful. Experts also organise their knowledge quite differently from novices.
Organisation: In 1982 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. As it turned out the students tended to group the problems based on their surface structure (similarities of objects used in the problem, e.g. on sketches illustrating the problem), whereas the professors used their deep structure (the general physical principles that underlay the problems) as criteria. By recognising the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g. another problem they solved earlier which required the same strategy).
Analysis: Experts often spend more time analysing a problem before actually trying to solve it. This way of approaching a problem may often result in what appears to be a slow start, but in the long run this strategy is much more effective. A novice, on the other hand, might start working on the problem right away, but often has to realise that he reaches dead ends as he chose a wrong path in the very beginning.
Creative Cognition[edit | edit source]
We already introduced a lot of ways to solve a problem, mainly strategies that can be used to find the “correct” answer. But there are also problems which do not require a “right answer” to be given – It is time for creative productiveness!
Imagine you are given three objects – your task is to invent a completely new object that is related to nothing you know. Then try to describe its function and how it could additionally be used. Difficult? Well, you are free to think creatively and will not be at risk to give an incorrect answer. For example think of what can be constructed from a half-sphere, wire and a handle. The result is amazing: a lawn lounger, global earrings, a sled, a water weigher, a portable agitator, ... [2]
Divergent Thinking[edit | edit source]
The term divergent thinking describes a way of thinking that does not lead to one goal, but is open-ended. Problems that are solved this way can have a large number of potential 'solutions' of which none is exactly 'right' or 'wrong', though some might be more suitable than others.
Solving a problem like this involves indirect and productive thinking and is mostly very helpful when somebody faces an ill-definedproblem, i.e. when either initial state or goal state cannot be stated clearly and operators or either insufficient or not given at all.
The process of divergent thinking is often associated with creativity, and it undoubtedly leads to many creative ideas. Nevertheless, researches have shown that there is only modest correlation between performance on divergent thinking tasks and other measures of creativity. Additionally it was found that in processes resulting in original and practical inventions things like searching for solutions, being aware of structures and looking for analogies are heavily involved, too.
Thus, divergent thinking alone is not an appropriate tool for making an invention. You also need to analyse the problem in order to make the suggested, i.e. invention, solution appropriate.
right or wrong[edit | edit source]
The ability of children to imitate the people and the surrounding environment also influential in recognizing the concepts of right and wrong To introduce the concepts of right and wrong must be seen from the age of the child. When children are a year old, their brains are not fully developed so their understanding is still limited. But keep in mind, too, from an early age the average child is able to imitate parents, see their surroundings and do imitation or called modeling. Therefore, the introduction of the concept of right and wrong also depends on how the parents or other adults live with the child. "If a mother often sits on the couch while raising both legs, children tend to sit with more or less the same style and think this is true. As we get older, modeling is the most natural thing that children can get about right and wrong," said this psychologist called Kiki. The method of giving understanding about the concepts of right and wrong is also adjusted to the age of the child. If children are still toddlers, they can go through activities such as telling stories that are rich in social values. Slip conclusions at the end of a fairy tale. "For example, the Kancil tale, after storytelling parents can say, 'So, stealing is not good', to emphasize the moral message in the fairy tale," said the psychologist from the Indonesian Psychological Practice Foundation, Bintaro, South Jakarta. For children who are older, for example in primary school age and still under 12 years of age, understanding can be given by giving an explanation of their eyes. Because the nature of them still tends to be egocentric. However, when entering adolescence, giving an explanation can be through a general perspective, especially cause and effect. "When giving to tell children about the concepts of right and wrong, parents need to pay attention to whether the child really understands the message that was delivered as a whole or only part of the contents of the message," Kiki added. For example, when parents want to teach the concept of stealing is not good through the story of Kancil, parents must make sure the child understands that anyone should not steal, no matter what the circumstances. Do not let the child who understands that is not allowed to steal a mouse deer or that should not be stolen is cucumber. Therefore, ask the child to explain his understanding once more so that the child is sure to understand. Responsible Learning If you have been taught the concept of right and wrong, but the child still violates it, parents must act and the child needs to know the consequences of the wrong actions. "For example, it was explained that you should not pick rambutan from a neighboring tree, but the child still did it, immediately reprimanded firmly and words that were not ambiguous or ambiguous, but still polite. "However, the child must be responsible for his attitude," Kiki reminded. Of course, continued Kiki, all this depends on the age of the child. In a small age for certain things, it is better for parents to stay with children, but when they are older, children need to know that parents will not risk their mistakes. Children who from childhood have understood between right and wrong will grow into individuals who are independent, responsible and well-mannered. This will also make it easier for them to socialize in their environment, have healthy friendships and make it easier for them to get good jobs because employers and coworkers certainly want to work with people who are polite, honest and responsible. Important to remember The following basic things can be done by parents to instill in children the right behavior - To say thanks - Say a word please if you want to ask for help - apologize if wrong, even to the child if the parents are wrong - Say greetings
Convergent Thinking[edit | edit source]
Convergent thinking patterns are problem solving techniques that unite different ideas or fields to find a solution. The focus of this mindset is speed, logic and accuracy, also identification of facts, reapplying existing techniques, gathering information. The most important factor of this mindset is: there is only one correct answer. You only think of two answers, namely right or wrong. This type of thinking is associated with certain science or standard procedures. People with this type of thinking have logical thinking, are able to memorize patterns, solve problems and work on scientific tests. Most school subjects sharpen this type of thinking ability.
Research shows that the creative process involves both types of thought processes. But experts recommend not joining the two processes in one session. For example, in the next 30 minutes, you invite everyone on your team to brainstorm creating new ideas (which involve divergent thinking patterns). Within 30 minutes, all ideas should only be recorded, not judged, for example by saying that an idea is irrelevant because of a limited budget. After all the ideas are contained, go to the next session, namely analysis and decision making (which involves convergent thinking patterns). Based on research too, doing creative jobs causes mood swings (mood swings), and it turns out that both types of thinking create two different moods. Convergent thinking patterns create negative moods, while divergent thinking patterns create a positive mood. J.A. Research Horne in 1988 revealed that lack of sleep will greatly affect the performance of people with divergent thought patterns, whereas people with convergent mindsets will be more likely to be fine. Including which mindset do you have? Use wisely your talents, and practice both types of thinking to be able to use them in balance at the right times.
Neurophysiological Background[edit | edit source]
Presenting Neurophysiology in its entirety would be enough to fill several books. Fortunately we do not have to concern ourselves with most of these facts. Instead, let's just focus on the aspects that are really relevant to problem solving. Nevertheless this topic is quite complex and problem solving cannot be attributed to one single brain area. Rather there are systems of several brain areas working together to perform a specific task. This is best shown by an example:
- In 1994 Paolo Nichelli and coworkers used the method of PET (Positron Emission Tomography), to localise certain brain areas, which are involved in solving various chess problems. In the following table you can see which brain area was active during a specific task:
| Task | Location of Brain activity |
|---|---|
|
(also called the "what"-pathway of visual processing)
(also called the "where"-pathway of visual processing)
(forming new memories)
|

One of the key tasks, namely planning and executing strategies, is performed by a brain area which also plays an important role for several other tasks correlated with problem solving – the prefrontal cortex (PFC). This can be made clear if you take a look at several examples of damages to the PFC and their effects on the ability to solve problems.
Patients with a lesion in this brain area have difficulty switching from one behaviouristic pattern to another. A well known example is the wisconsin card-sorting task. A patient with a PFC lesion who is told to separate all blue cards from a deck, would continue sorting out the blue ones, even if the experimenter told him to sort out all brown cards. Transferred to a more complex problem, this person would most likely fail, because he is not flexible enough to change his strategy after running into a dead end.
Another example is the one of a young homemaker, who had a tumour in the frontal lobe. Even though she was able to cook individual dishes, preparing a whole family meal was an infeasible task for her.
As the examples above illustrate, the structure of our brain seems to be of great importance regarding problem solving, i.e. cognitive life. But how was our cognitive apparatus designed? How did perception-action integration as a central species specific property come about?
The Evolutionary Perspective[edit | edit source]
Charles Darwin developed the evolutionary theory which was primarily meant to explain why there are so many different kinds of species. This theory is also important for psychology because it explains how species were designed by evolutionary forces and what their goals are. By knowing the goals of species it is possible to explain and predict their behaviour.
The process of evolution involves several components, for instance natural selection – which is a feedback process that 'chooses' among 'alternative designs' on the basis of deciding how good the respective modulation is. As a result of this natural selection we find adaption. This is a process that constantly tests the variations among individuals in relation to the environment. If adaptions are useful they get passed on; if not they’ll just be an unimportant variation.
Another component of the evolutionary process is sexual selection, i.e. increasing of certain sex characteristics, which give individuals the ability to rival with other individuals of the same sex or an increased ability to attract individuals of the opposite sex.
Altruism is a further component of the evolutionary process, which will be explained in more detail in the following chapter Evolutionary Perspective on Social Cognitions.
Summary and Conclusion[edit | edit source]
After Knut read this WikiChapter he was relieved that he did not waste his time for the essay – quite the opposite! He now has a new view on problem solving – and recognises his problem as a well-defined one:
His initial state was the clear blank paper without any philosophical sentences on it. The goal state was just in front of his mind's eye: Him – grinning broadly – handing in the essay with some carefully developed arguments.
He decides to use the technique of Means-End Analysis and creates several subgoals:
- 1. Read important passages again
- 2. Summarise parts of the text
- 3. Develop an argumentative structure
- 4. Write the essay
- 5. Look for typos
Right after he hands in his essay Knut will go on reading this WikiBook. He now looks forward to turning the page over and to discovering the next chapter...
References[edit | edit source]
- ↑ R.L. Dominowski and P. Dallob, Insight and Problem Solving. In The Nature of Insight, R.J. Sternberg & J.E. Davidson (Eds). MIT Press: USA, pp.33-62 (1995).
- ↑ Goldstein, E.B. (2005). Cogntive Psychology. Connecting Mind, Research, and Everyday Experience. Belmont: Thomson Wadsworth.
External links[edit | edit source]
- Mental Models, by Philip N. Johnson-Laird
Organizational Stuff[edit | edit source]
- send eMail to all
- anwinkle
- benkuest
- lkaestne
- nmoeller
- tgrage