Circuit Theory/Time Constants
Homogeneous equations are exponential. A homogeneous differential equation is discharging or charging (0 value constant DC source). A non-homogeneous differential equation has a sinusoidal source. It can be solved by splitting into a homogeneous solution plus a particular solution. The steady state solutions earlier were particular solutions.
- homogeneous equation ⇒ discharging (DC source) ⇒ homogeneous solution
- non-homogeneous equation ⇒ AC source ⇒ particular (steady state) + homogeneous (discharging) solution
The proof of the exponential solution to the discharging circuit is is hard:
- guess solution
- see if it is possible
- if possible assume it is the solution
In this case it works because there is only one guess:

that we know of.
A first order differential looks like this:
A solution is:
- (Gödel proved that there are always other truths possible. We can not be certain this is the only solution.)
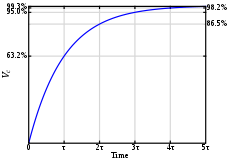
Tau, τ, or has a name:
- = time constant
The Steady State(particular) definition is:
since for charging and discharging:
Try to write all answers in the form of
instead of:
The reason is: looking at a number and taking the inverse of it is hard. This makes it hard to look at an equation and "see" it's time constant.
The units of any time constant are seconds. In circuits with both inductors and capacitors, there are two time constants that are called "zeros". They are called zero's because they are solutions to the particular solution which sets the differential to zero. They are given the symbol "s" and are identical to the complex frequency concept.





