Circuit Theory/Extra Element
The Extra Element technique helps break down one complicated problem into several simpler ones like superposition. However the goal is to find impedance rather than current or voltage.
By removing the element that most complicates the circuit the overall circuit impedance can be obtained.
where
- is the impedance chosen as the extra element to be removed
- is the input impedance with Z removed (or made infinite)
- is the impedance seen by the extra element Z with the source shorted (or made zero)
- is the impedance seen by the extra element Z with the source opened (or made infinite)
Computing these three terms may seem like extra effort, but they are often easier to compute than the overall input impedance.
Example
[edit | edit source]


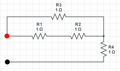
Consider the problem of finding for the circuit in Figure 1 using the EET (note all component values are unity for simplicity). If the capacitor (gray shading) is denoted the extra element then
Removing this capacitor from the circuit we find
-
capacitor removed, looking at the input (source input)
-
capacitor removed, reorganizing circuit so can see input impedance
Calculating the impedance seen by the capacitor with the input shorted we find
-
shorted source, finding
-
shorted source redrawn
Calculating the impedance seen by the capacitor with the input open we find
-
open source, finding
-
open source redrawn
Therefore using the EET, we find
Note that this problem was solved by calculating three simple driving point impedances by inspection.