Chemical Sciences: A Manual for CSIR-UGC National Eligibility Test for Lectureship and JRF/Mössbauer spectroscopy
| This page was imported and needs to be de-wikified. Books should use wikilinks rather sparsely, and only to reference technical or esoteric terms that are critical to understanding the content. Most if not all wikilinks should simply be removed. Please remove {{dewikify}} after the page is dewikified. |

Mössbauer spectroscopy (Template:Lang-de) is a spectroscopic technique based on the recoil-free, resonant absorption and emission of gamma rays in solids. This resonant emission and absorption was first observed by Rudolf Mössbauer during his graduate studies in 1957, and is called the Mössbauer effect in his honor. Mössbauer received a Nobel Prize in 1961 for this work.[1] [2]
Like NMR spectroscopy, Mössbauer spectroscopy probes tiny changes in the energy levels of an atomic nucleus in response to its environment. Typically, three types of nuclear interaction may be observed: an isomer shift, also known as a chemical shift; quadrupole splitting; and, magnetic or hyperfine splitting, also known as the Zeeman effect.[3] Due to the high energy and extremely narrow line widths of gamma rays, Mössbauer spectroscopy is one of the most sensitive techniques in terms of energy (and hence frequency) resolution, capable of detecting change in just a few parts per 1011.[1]
Basic principle[edit | edit source]
Just as a gun recoils when a bullet is fired, conservation of momentum requires a free nucleus (such as in a gas) to recoil during emission or absorption of a gamma ray. If a nucleus at rest emits a gamma ray, the energy of the gamma ray is slightly less than the natural energy of the transition, but in order for a nucleus at rest to absorb a gamma ray, the gamma ray's energy must be slightly greater than the natural energy, because in both cases energy is lost to recoil. This means that nuclear resonance (emission and absorption of the same gamma ray) is unobservable with free nuclei, because the shift in energy is too great and the emission and absorption spectra have no significant overlap.[1]
Nuclei in a solid crystal, however, are not free to recoil because they are bound in place in the crystal lattice. When a nucleus in a solid emits or absorbs a gamma ray, some energy can still be lost as recoil energy, but in this case it always occurs in discrete packets called phonons (quantized vibrations of the crystal lattice). Any whole number of phonons can be emitted, including zero, which is known as a "recoil-free" event. In this case conservation of momentum is satisfied by the momentum of the crystal as a whole, so practically no energy is lost.
As an analogy, imagine jumping from a boat to shore, and imagine that the distance from boat to shore is the longest you can possibly jump (on land). If the boat is floating in water, you will fall short because some of your energy goes into pushing the boat back. If the water is frozen solid, however, you will be able to make it. [4]
Mössbauer found that a significant fraction of emission and absorption events will be recoil-free, which is quantified using the Lamb–Mössbauer factor.[5] This fact is what makes Mössbauer spectroscopy possible, because it means gamma rays emitted by one nucleus can be resonantly absorbed by a sample containing nuclei of the same isotope, and this absorption can be measured.
Typical method[edit | edit source]
In its most common form, Mössbauer absorption spectroscopy, a solid sample is exposed to a beam of gamma radiation, and a detector measures the intensity of the beam transmitted through the sample. The atoms in the source emitting the gamma rays must be of the same isotope as the atoms in the sample absorbing them.
If the emitting and absorbing nuclei were in identical chemical environments, the nuclear transition energies would be exactly equal and resonant absorption would be observed with both materials at rest. The difference in chemical environments, however, causes the nuclear energy levels to shift in a few different ways, as described below. Although these energy shifts are tiny (often less than a micro-electronvolt), the extremely narrow spectral linewidths of gamma rays for some radionuclides make the small energy shifts correspond to large changes in absorbance. To bring the two nuclei back into resonance it is necessary to change the energy of the gamma ray slightly, and in practice this is always done using the Doppler effect.
During Mössbauer absorption spectroscopy, the source is accelerated through a range of velocities using a linear motor to produce a Doppler effect and scan the gamma ray energy through a given range. A typical range of velocities for 57Fe, for example, may be ±11 mm/s (1 mm/s = 48.075 neV).[1] [5]
In the resulting spectra, gamma ray intensity is plotted as a function of the source velocity. At velocities corresponding to the resonant energy levels of the sample, a fraction of the gamma rays are absorbed, resulting in a drop in the measured intensity and a corresponding dip in the spectrum. The number, positions, and intensities of the dips (also called peaks; dips in transmitted intensity are peaks in absorbance) provide information about the chemical environment of the absorbing nuclei and can be used to characterize the sample.
Selecting a suitable source[edit | edit source]
Mössbauer spectroscopy is limited by the need for a suitable gamma-ray source. Usually, this consists of a radioactive parent that decays to the desired isotope. For example, the source for 57Fe consists of 57Co, which decays by electron capture to an excited state of 57Fe, then subsequently decays to a ground state emitting the desired gamma-ray. Ideally the parent isotope will have a sufficiently long half-life to remain useful, but will also have a sufficient decay rate to supply the required intensity of radiation. Also, the gamma-ray energy should be relatively low, otherwise the system will have a low recoil-free fraction resulting in a poor signal-to-noise ratio and requiring long collection times. The periodic table below indicates those elements having an isotope suitable for Mössbauer spectroscopy. Of these, 57Fe is by far the most common element studied using the technique, although 129I, 119Sn, and 121Sb are also frequently studied.
Analysis of Mössbauer spectra[edit | edit source]
As described above, Mössbauer spectroscopy has an extremely fine energy resolution and can detect even subtle changes in the nuclear environment of the relevant atoms. Typically, there are three types of nuclear interactions that are observed, isomer shift (or chemical shift), quadrupole splitting and hyperfine splitting (or Zeeman splitting). [3]Invalid parameter in <ref> tag
Isomer shift is a relative measure describing a shift in the resonance energy of a nucleus due to the transition of electrons within its s orbital. The whole spectrum is shifted in either a positive or negative direction depending upon the s electron charge density. This change arises due to alterations in the electrostatic response between the non-zero probability s orbital electrons and the non-zero volume nucleus they orbit.
Only electrons in s orbitals demonstrate non-zero probability because their 3D spherical shape incorporates the volume taken up by the nucleus. However, the p, d, and other electrons may influence the s electron density through a screening effect. The s electron density can also be affected by the oxidation state and the chemical environment of the atom.
Isomer shift (chemical shift, C.S.) can be expressed using the formula below, where K is a nuclear constant, the difference between Re2 and Rg2 is the effective nuclear charge radius difference between excited state and the ground state, and the difference between [Ψs2(0)]a and [Ψs2(0)]b is the electron density difference on the nucleus.
C.S. = K (Re2-Rg2) {[Ψs2(0)]a - [Ψs2(0)]b}

The physical meaning of this equation can be clarified using examples:
- While an increase in s electron density in 57Fe spectrum gives a negative shift because the change in the effective nuclear charge is negative an increase in s electron density in 119Sn gives a positive shift due to a positive change in overall nuclear charge.
- Oxidised ferrous ions (Fe3+) have larger positive isomer shifts than ferric ions (Fe2+) because s electron density at the nucleus of ferrous ions is less due to a greater screening effect by d electrons.[6]
Quadrupole Splitting reflects the interaction between the nuclear energy levels and surrounding electric field gradient (EFG). Nuclei in states with non-spherical charge distributions, i.e. all those with angular quantum number (I) greater than 1/2, produce an asymmetrical electric field which splits the nuclear energy levels. This produces a nuclear quadrupole moment.[3]
In the case of an isotope with a I=3/2 excited state, such as 57Fe or 119Sn, the 3/2 to 1/2 transition is split into two substates mI=±1/2 and mI=±3/2. Thess appear as two specific peaks in a spectrum, sometimes referred to as a 'doublet'. Quadrupole splitting is measured as the separation between these two peaks and reflects the character of the electric field at the nucleus.

Magnetic Splitting (hyperfine splitting) is a result of the interaction between the nucleus any surrounding magnetic field. A nucleus with spin, I, splits into 2I + 1 sub-energy levels in the presence of magnetic field. For example, a nucleus with spin state I= 3/2 will split into 4 non-degenerate sub-states with mI values of +3/2, +1/2, -1/2 and -3/2. Each split is hyperfine, being in the order of 10-7eV. The restriction rule of magnetic dipoles means that transitions between the excited state and ground state can only occur where mI changes by 0 or 1. This gives six possible transitions for a 3/2 to 1/2 transition.[3] Generally speaking therefore, in the majority of cases only six peaks can be monitored in a spectrum produced by a hyperfine splitting nucleus.
The three Mössbauer parameters: isomer shift, quadrupole splitting, and hyperfine splitting can often be used to identify a particular compound by comparing it to known spectra. A large database including most of the published Mössbauer parameters available in the literature is maintained by the Mössbauer Effect Data Center.[7] In some cases, a compound may have more than one possible crystal structure. For example, the crystal structure of hematite (Fe2O3) supports two unique sites for each of the six iron atoms. The corresponding spectrum therefore has twelve peaks, two for each potential atomic site. Thus, hematite also has two sets of Mössbauer parameters, one for each site.
In addition, the relative intensities of the various peaks reflect the relative concentrations of compounds in a sample and can be used for semi-quantitative analysis. Also, since ferromagnetic phenomena are size-dependent, in some cases spectra can provide insight into the crystallite size and grain structure of a material.
Applications of Mössbauer spectroscopy[edit | edit source]
Among the drawbacks of the technique are the limited number of gamma ray sources and the requirement that samples be solid in order to eliminate the recoil of the nucleus. Mössbauer spectroscopy is unique in its sensitivity to subtle changes in the chemical environment of the nucleus including oxidation state changes, the effect of different ligands on a particular atom, and the magnetic environment of the sample.
As an analytical tool Mössbauer spectroscopy offers detection limits in the order of billionths of an electron volt.[3]. It has been especially useful in the field of geology for identifying the composition of iron-containing specimens including meteors and moon rocks. In situ data collection of Mössbauer spectra has also been carried out on iron rich rocks on Mars.[8]
Another significant application of Mössbauer spectroscopy is the study of phase transformations that occur in iron catalysts during Fischer–Tropsch synthesis. While these catalysts initially consist of hematite (Fe2O3), during reaction they are transformed into a mixture of magnetite (Fe3O4) and several iron carbides. The formation of carbides appears to improve catalytic activity, however it can also lead to the mechanical break-up and attrition of the catalyst particles. This can cause difficulties in the final separation of catalyst from reaction products.[9]
Mössbauer spectroscopy has also been used to determine the relative concentration change in the oxidation state of antimony (Sb) during the selective oxidation of olefins. During calcination all the Sb ions in an antimony-containing tin dioxide catalyst transform into the +5 oxidation state. Following the catalytic reaction, almost all Sb reverts from +5 to a +3 oxidation state. A significant change in the chemical environment surrounding the antimony nucleus occurs during the oxidation state change which can easily be monitored as an isomer shift in the Mössbauer spectrum.[10]
This technique has also been used to observe the second-order transverse Doppler effect predicted by the theory of relativity, because of very high energy resolution.[11]
More recently, Mössbauer spectroscopy has been instrumental in developing an understanding of the structure and function of iron containing enzymes and the model complexes synthesized to mimic the functions of these enzymes. Some examples of enzymes characterised in this way are: ribonucleotide reductase[12][13] methane monooxygenase,[14][15] tryptophan dioxygenase,[16] deoxypusine hydroxylase,[17] protocatechuate 2,3 dioxygenase,[18] and cytochrome ba3.[19]
Mossbauer spectroscopy has also been used very successfully to investigate the electronic structure of heterobimetallic complexes.[20][21][22][23]
Mössbauer spectrometers[edit | edit source]
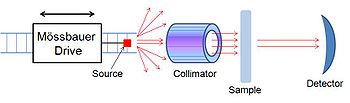
A Mössbauer spectrometer is a device that performs Mössbauer spectroscopy, or a device that uses the Mössbauer effect to determine the chemical environment of Mössbauer nuclei present in the sample. It is formed by three main parts; a source that moves back and forth to generate a doppler effect, a collimator that filters out non-parallel gamma rays and a detector.
A miniature Mössbauer Spectrometer, named (MB) MIMOS II, was used by the two rovers in NASA's Mars Exploration Rover missions.[24]
Notes on 57Fe Mössbauer spectroscopy[edit | edit source]

The Mössbauer parameters: chemical isomer shift and quadrupole splitting, are generally evaluated with respect to a reference material. For example, in iron compounds, the Mössbauer parameters were evaluated using iron foil (thickness less than 40 micrometers). The centroid of the six lines spectrum from metallic iron foil is −0.1 mm/s (for Co/Rh source). All shifts in other iron compounds are computed relative to this −0.10 mm/s (at room temperature), i.e., in this case isomer shifts are relative to Co/Rh source. In other words, the centre point of the Mössbauer spectrum is zero. The shift values may also be reported relative to 0.0 mm/s, here shifts are relative to the iron foil.
To calculate outer line distance from six line iron spectrum:
where c is the velocity of light in m/s, Hint is the internal magnetic field of the metallic iron (33 T), μN is the nuclear magneton (3.1524512326×10−8 eV/T), Eγ is the excitation energy (14.412497 keV), gn is the ground state nuclear splitting factor (0.09062/I, where I = 1⁄2) and g*n is the excited state splitting factor of 57Fe (0.1549/I, where I = 3⁄2).
By substituting the above values one would get V = 10.62 mm/s.
Other values are sometimes used to reflect different qualities of iron foils. In all cases any change in V only affects the quadrupole splitting and not the isomer shift. As the IBAME, the authority for Mössbauer spectroscopy, does not specify a particular value, anything between 10.60 mm/s to 10.67 mm/s can be used.
References[edit | edit source]
- ↑ a b c d Mössbauer Spectroscopy Group, Royal Society of Chemistry (RSC) website, Introduction to Mössbauer Spectroscopy Part 1 Accessed June 3 2010
- ↑ P. Gütlich, J.M. Greneche, F.J. Berry; Mössbauer Spectroscopy: A Powerful Tool in Scientific Research Accessed June 3 2010
- ↑ a b c d e Mössbauer Spectroscopy Group, Royal Society of Chemistry (RSC) website, Introduction to Mössbauer Spectroscopy Part 2 Accessed June 3 2010
- ↑ International Board on the Applications of the Mössbauer Effect (IBAME) and Mössbauer Effect Data Center (MEDC), Mössbauer Effect website Accessed June 3 2010
- ↑ a b Gütlich, J.M.; The Principle of the Mössbauer Effect and Basic Concepts of Mössbauer Spectrometry
- ↑ L. R. Walker, G. K. Wertheim, and V. Jaccarino, Phys. Rev. Lett., 6, 98, (1961)
- ↑ Mössbauer Effect Data Center
- ↑ G. Klingelhöfer (2004). "Mössbauer in situ studies of the surface of Mars". Hyperfine Interactions. 158: 117–124. doi:10.1007/s10751-005-9019-1.
- ↑
A. Sarkar; et al. (2007). "Fischer–Tropsch Synthesis: Characterization Rb Promoted Iron Catalyst". Catalysis Letters. 121: 1–11. doi:10.1007/s10562-007-9288-1.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑ Burger et al; 1986, Mössbauer spectroscopic study of the oxidation state of antimony in antimony sulfides of different composition, Journal of Chemical Crystallography, Volume 16, No. 2, pp 295-299, DOI: 10.1007/BF01161115
- ↑ Y.-L. Chen, D.-P. Yang (2007). "Recoilless Fraction and Second-Order Doppler Effect". Mössbauer Effect in Lattice Dynamics. John Wiley & Sons. doi:10.1002/9783527611423.ch5. ISBN 9783527611423.
- ↑
J.B. Lynch; et al. (1989). "Mössbauer and EPR studies of the binuclear iron center in ribonucleotide reductase from Escherichia coli. A new iron-to-protein stoichiometry". Journal of Biological Chemistry. 264: 8091–8096.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
T.E. Elgren; et al. (1990). "Electron Transfer Associated with Oxygen Activation in the B2 Protein of Ribonucleotide Reductase from E. Coli". Journal of Biological Chemistry. 266: 19265–19268.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
B.G. Fox; et al. (1988). "Evidence for a mu-oxo bridged binuclear iron center in the hydroxylase component of methane monooxygenase. Mössbauer and EPR studies". Journal of Biological Chemistry. 263: 10553–10556.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
B.G. Fox; et al. (1993). "Mössbauer, EPR, and ENDOR Studies of the Hydroxylase and Reductase Components of Methane Monooxygenase from Methylosinus Trichosporium OB3B". Journal of the American Chemical Society. 115: 3688–3701. doi:10.1021/ja00062a039.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
R. Gupta; et al. (2010). "EPR and Mössbauer spectroscopy show inequivalent hemes in tryptophan dioxygenase". Journal of the American Chemical Society. 132 (3): 1089–1109. doi:10.1021/ja908851e.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
V.V. Vu; et al. (2009). "Human deoxyhypusine hydroxylase, an enzyme involved in cell growth,activates O2 with a nonheme diiron center". Proceedings of the National Academy of Sciences. 106 (35): 14814–14819. doi:10.1073/pnas.0904553106.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
S.A. Volgel; et al. (1993). "Purification and Characterization of Protocatechuate 2,3 Dioxygenase from Bacillus macerans: a New Extradiol Catecholic Dioxygenase". Journal of Bacteriology. 175: 4414–4426.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
B.H. Zimmermann; et al. (1988). "Properties of a Copper-Containing Cytochrome ba3: A Second Terminal Oxidase from the Extreme Thermophile Thermus thermophilus". Proceedings of the National Academy of Sciences. 85: 5779–7783.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
C. Juarez-Garcia; et al. (1991). "Combined Moessbauer and EPR studies of the S = 3 state of an exchange-coupled iron(III)-copper(II) complex: test for quantitative EPR analysis of integer spin systems". Journal of the American Chemical Society. 113 (2): 518–525.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
T.R. Holman; et al. (1990). "Models for iron-oxo proteins. Moessbauer and EPR study of an antiferromagnetically coupled iron(III)-nickel(III) complex". Journal of the American Chemical Society. 112 (21): 7611–7618. doi:10.1021/ja00177a024.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
S. Menage; et al. (1990). "Models for Iron-Oxo Proteins: Dioxygen Binding to a Diferrous Complex". Journal of the American Chemical Society. 112: 6423–6425. doi:10.1021/ja00173a055.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
J. Kaizer; et al. (2004). "Stable Nonheme FeIVO Complexes That Can Oxidize C-H Bonds of Cyclohexane at Room Temperature". Journal of the American Chemical Society. 126: 472–473. doi:10.1021/ja037288n.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑
G. Klingelhöfer; et al. (2002). "The miniaturized Mössbauer spectrometer MIMOS II for extraterrestrial and outdoor terrestrial applications: A status report". Hyperfine Interactions. 144: 371–379. doi:10.1023/A:1025444209059.
{{cite journal}}: Explicit use of et al. in:|author=(help)
