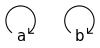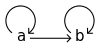Category Theory/Categories
This is the Categories chapter of Category Theory.
Definition
[edit | edit source]A category consists of four kinds of data subject to three axioms, as listed below:
Data
[edit | edit source]- Objects
- has objects denoted by , , ,…
- Morphisms
- For each ordered pair of objects , in , there is a class of morphisms or arrows from to . The notation means that is a morphism from to . The class of all morphisms from to is denoted by or sometimes simply .
- Composition
- For each ordered triple of objects , , in , there is a law of composition: If and , then the composite of and is a morphism
- Identity
- For each object there is a designated identity morphism on , notated as , from to .
Axioms
[edit | edit source]These data satisfy the following three axioms, of which the first is in the nature of a convention, while the remaining two are more substantial:
- Unique typing
- and are disjoint unless , .
- Associative Law
- if the composites are defined. Note that if one composite is defined, the other is necessarily defined.
- Identity is a “neutral element”
- For the identity morphism associated to each object , two equations must hold for each pair of objects and and each pair of arrows , :
Terminology and fine points
[edit | edit source]- If in a category, is called the domain or source of , and is called the codomain or target of .
- is called a hom class (or a hom set if it is indeed a set). In general a hom set may be empty, but for any object , is not empty because it contains the identity morphism.
- The hom class may be denoted by or if it is necessary to specify which category is referred to.
- An object in a category need not be a set; the object need not have anything called elements.
- Morphisms may also be called maps. This does not mean that every morphism in any category is a set function (see #Baby examples and #Preorders). Arrow is a less misleading name.
- The composite may be written .
- It might be more natural to write the composite of and as instead of but the usage given here is by far the most common. This stems from the fact that if the arrows are set functions and , then . Thus is best read as "do after ".
Large and small
[edit | edit source]The definition says that a category 'has' objects and 'has' morphisms. This means that for any category and is any mathematical object, the statement ' is an object of ' is either true or false, and similarly for the statement ' is a morphism of '. The objects (or arrows) of a category need not constitute a set. If they do, the category is said to be small. If they don't, the category is large.
The requirement that the collection of morphisms from to be a set makes a category locally small. In this book, all categories are locally small.
Discrete
[edit | edit source]A category is discrete if every morphism is an identity.
Preorder
[edit | edit source]A category is a preorder if for every pair of objects , there exists at most one morphism .
Examples of categories
[edit | edit source]Baby examples
[edit | edit source]These examples are trivial and maybe uninteresting. But do not underestimate the power of baby examples. For one thing, they are sometimes counterexamples to possible theorems.
- 0 (the empty category)
- This category has no objects and no morphisms.
- 1

- The category 1 has one object and one morphism, which must necessarily be the object's identity arrow.
- 1+1
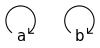
- This category has two objects and two morphisms: the identities on each object.
- 2
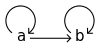
- This category has two objects and three morphisms. The third morphism goes from one object to the other.
- The objects of these baby categories are nodes in a graph (not sets) and the morphisms are arrows in the graph (not functions).
- For these baby categories we don't have to say what the composition operation does: it is always forced.
- It is impolite to say that categorists think that 1 + 1 is not equal to 2.
The category of sets
[edit | edit source]The category of sets, denoted by Set, is this category:
- The objects are all sets
- A morphism from a set to a set is a function with domain and codomain .
- The composition is the usual composition: If and then is defined by for all .
- The identity morphism on a set is the identity function defined by for .
- In order to preserve the unique typing in a function definition, it is necessary to include its codomain. For example, is a different function from the inclusion function to some set properly including .
- In most approaches to the foundations of math, the collection of all sets is not a set. This makes Set a large category. However, it is still locally small since the class of all functions between two sets, and is a subclass of the power set of their Cartesian product which is by definition a set.
Mathematical structures as categories
[edit | edit source]Preorders
[edit | edit source]A preorder on a set is a reflexive and transitive relation on , which means that for all , and for all , , in , if and , then .
A preorder "is" a category in the following sense: Given a preorder (, ) the category structure is this:
- The objects of the category are the elements of .
- There is exactly one morphism from to if and only if .
The existence of identities is forced by reflexivity and the composition law is forced by transitivity. It follows that the category structure has the property that there is at most one morphism from any object to any object .
Conversely, suppose you have a category with set of objects, with the property that there is at most one morphism between any two objects. Define a relation on by requiring that if and only if there is a morphism from to . Then (, ) is a preorder.
The statements in the two preceding paragraphs describe an equivalence of categories between the category of small categories with at most one morphism between any two objects and all functors between such categories, and the category of preorders and order-preserving maps.
Remark: Given a preorder, the morphisms of the corresponding category exist by definition. There is exactly one morphism from to if and only if . This is an axiomatic definition; in a model a morphism from to could be anything, for example the pair (, ). In no sense is the morphism required to be a function.
Groups
[edit | edit source]Every group can be viewed as a category as follows: has one single object; call it . Therefore it has only one homset , which is defined to be the underlying set of the group (in other words, the arrows are the group elements.) We take as composition the group multiplication. It follows that the identity element of is . Notice that in the category , every morphism is an isomorphism (invertible under composition). Conversely, any one-object category in which all arrows are isomorphisms can be viewed as a group; the elements of the group are the arrows and the multiplication is the composition of the category. This describes an equivalence between the category of groups and homomorphisms and the category of small categories with a single object in which every morphism is an isomorphism.
This can be generalized in two ways.
A category is called a groupoid if every morphism is an isomorphism. Thus a groupoid can be called "a group with many objects."
A monoid is a set with an associative binary operation that has an identity element. By the same technique as for groups, any monoid "is" a category with exactly one object and any category with exactly one object "is" a monoid.
Matrices
[edit | edit source]This is a good example of a category whose objects are not sets and whose arrows are not functions. is the category whose objects are the positive integers and whose arrows are matrices where composition is matrix multiplication, for any commutative ring . For any object , , the identity matrix.
Categories of sets with structure
[edit | edit source]| This section is a stub. You can help Wikibooks by expanding it. |
- finite sets and functions; denoted FinSet.
- monoids and morphisms; denoted Mon.
- groups and homomorphisms; denoted Grp.
- abelian groups and homomorphisms; denoted Ab.
- rings and unit-preserving homomorphisms; denoted Rng.
- commutative rings and unit-preserving homomorphisms; denoted CRng.
- left modules over a ring and linear maps; denoted -Mod.
- right modules over a ring and linear maps; denoted Mod-.
- modules over a commutative ring and linear maps; denoted -Mod.
- subsets of Euclidean space of 3 dimensions and Euclidean movements
- subsets of Euclidean space of n dimensions and continuous functions
- topological spaces and continuous functions; denoted Top.
- topological spaces and homotopy classes of functions; denoted Toph.
The law of composition is not specified explicitly in describing these categories. This is the custom when the objects have underlying set-structure, the morphisms are functions of the underlying sets (transporting the additional structure), and the law of composition is merely ordinary function-composition. Indeed, sometimes even the specification of the morphisms is suppressed if no confusion would arise—thus one speaks of the category of groups.
The examples of sets with structure suggest a conceptual framework. For example, the concept of group may be regarded as constituting a first-order abstraction or generalization from various concrete, familiar realizations such as the additive group of integers, the multiplicative group of nonzero rationals, groups of permutations, symmetry groups, groups of Euclidean motions, and so on. Then, again, the notion of a category constitutes a second-order abstraction, the concrete realizations of which consist of such first-order abstractions as the category of groups, the category of rings, the category of topological spaces, and so on.
Properties of objects and morphisms
[edit | edit source]| This section is a stub. You can help Wikibooks by expanding it. |
Isomorphisms
[edit | edit source]A morphism in a category is said to be an isomorphism if there is a morphism in the category with , . It is easy to prove that is then uniquely determined by . The morphism is called the inverse of f, written . It follows that . If there is an isomorphism from to , we say is isomorphic to , and it is easy to prove that "isomorphism" is an equivalence relation on the objects of the category.
Examples
[edit | edit source]- A function from to in the category of sets is an isomorphism if and only if it is bijective.
- A homomorphism of groups is an isomorphism if and only if it is bijective.
- The isomorphisms of the category of topological spaces and continuous maps are the homeomorphisms. In contrast to the preceding example, a bijective continuous map from one topological space to another need not be a homeomorphism because its inverse (as a set function) may not be continuous. An example is the identity map on the set of real numbers, with the domain having the discrete topology and the codomain having the usual topology.
Monomorphisms and Epimorphisms
[edit | edit source]A morphism in a category is a monomorphism if, for any morphisms and , if and are defined and then .
A morphism in a category is an epimorphism if, for any morphisms and , if and are defined and then .
Initial and terminal objects
[edit | edit source]is said to be a terminal (or final) object when is a unique morphism for any in . The law of composition ensures that if and are terminal objects in , they are isomorphic, i.e., is unique up to isomorphism. In the categories of sets, groups, and topological spaces, the terminal objects are singletons, trivial groups, and one-point spaces, respectively. "b" is the terminal object in 2 as depicted above.
Constructions on categories
[edit | edit source]| This section is a stub. You can help Wikibooks by expanding it. |
Subcategories
[edit | edit source]A subcategory of a category is a category in which:
- The class of objects of is contained in the class of objects of .
- The class of arrows of is contained in the class of arrows of .
- For every arrow in , the domain and codomain of are in .
- For every object in , the identity arrow is in .
- For every pair of arrows in , the arrow is in where it is defined.
Opposite category
[edit | edit source]Given a category , the opposite (or dual) category has the same objects as and for every arrow in , the arrow is in . In other words, it has the same objects, and arrows are reversed.
The product of two categories
[edit | edit source]Given two categories and , the product category, denoted , is given by the following data:
- The objects of are where is an object of and is an object of .
- The arrows of are where is an arrow of and is an arrow of .
- Composition is given by .
The product is called the cylinder category, denoted .
Arrow categories
[edit | edit source]- A functor category is a category whose objects are functors and arrows are natural transformations.
- A functor category is called an arrow category, denoted . Its objects are arrows in and its arrows are pairs of arrows such that .
Comma categories
[edit | edit source]- Given categories and functors and , the comma category has objects where is an object in , is an object in , and is an arrow in . Its arrows are where is an arrow in and is an arrow in such that . Composition is given by . The identity is .
Special types of comma categories
[edit | edit source]Using the definition of comma category above, assume that we have , , and . Let denote the object in . Then for some object in . In this case, we write the comma category as and call it the slice category of (or the category of objects over ).
Now assume, instead, that we have , , and . Let denote the object in . Then for some object in . In this case, we write the comma category as and call it the coslice category of (or the category of objects under ).
Finally, if we have and , then the comma category .