Astrodynamics/Classical Orbit Elements
Orbit Parameters[edit | edit source]
It is possible to specify an orbit entirely using a set of 5 parameters. With these 5 parameters, we can specify precisely where an orbit is, how it is oriented in 3-D space, and what size it is. If we have an optional sixth parameter, we can determine exactly where the satellite is in its orbit at any arbitrary time t. These 6 parameters are called the Keplerian Elements.
However, before we discuss the 6 orbit parameters, we need to introduce a few new terms.
Angular Momentum[edit | edit source]
The vector that points from the center of the Earth to the satellite or object of interest is called r, and its velocity vector is called v. The vector that is perpendicular to both of these is called the specific angular momentum vector.
[angular momentum]
Ascending Node[edit | edit source]
The Earth's equator resides in a plane known as the fundamental plane (as it is in the geocentric-equatorial coordinate system, which we will be using in this section), and the orbit traced out by the vector r forms a plane known as orbital plane, which contains the vectors r and v. The line formed by the intersection of these two planes is known as the line of nodes.
We can find the vector n by taking the cross product of the angular momentum vector, h, and the unit vector K = <0, 0, 1>:
[ascending node]
n is a vector on the line of nodes that points in the direction of the ascending node. The ascending node is the spot where the satellite crosses the equatorial plane in a northerly direction. Likewise, the descending node is the point where the satellite crosses the equatorial plane in the southerly direction.
In an equatorial orbit, n is undefined, and there are no nodes.
Prograde and Retrograde[edit | edit source]
Prograde or direct means the satellite is traveling around the earth from west to east. Retrograde means the satellite is traveling from east to west. An object with an inclination between 0 and 90 degrees is orbiting or revolving in the same direction as the primary body is rotating. An object with an inclination of exactly 90 degrees has a perpendicular orbit which is neither prograde nor retrograde. An object with an inclination between 90 degrees and 180 degrees is in a retrograde orbit.
Visual Representation[edit | edit source]

This image shows two planes, the orbital plane (pale yellow) and the plane of reference (gray). The earth, or prime focus is considered to be at the dot at the center of the two planes. Notice how the orbit crosses the ecliptic at two points: once going northward (the ascending node), and once going southward (the descending node). The descending node is not marked in this picture, but its location should be obvious. We will explain some of the other terms below.
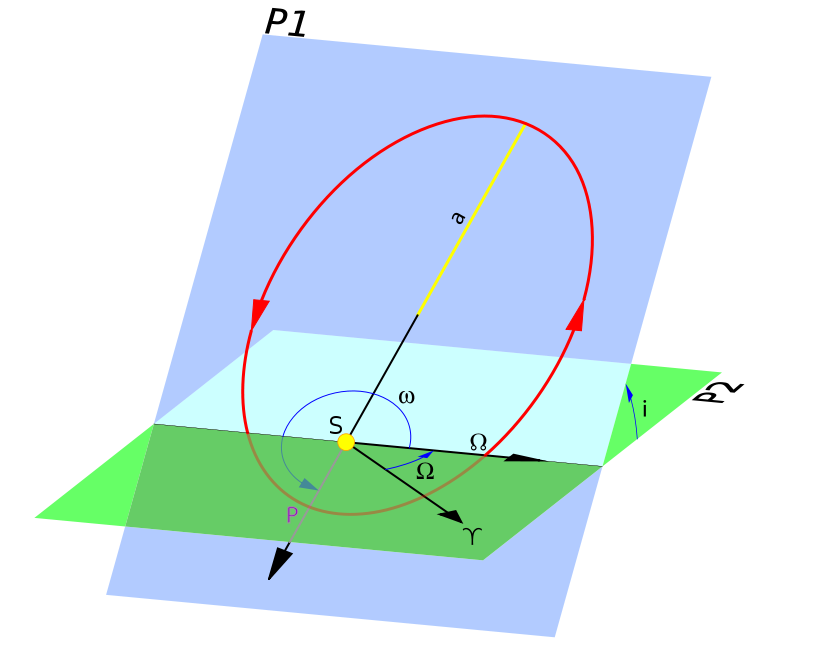
Classical Elements[edit | edit source]
Now that we have the node vector, along with the vectors r, v, and h, we can find our 5 classical orbital elements.
Semi-Major Axis[edit | edit source]
The semi-major axis, a can be found via the Vis-Viva equation:
Where some terms remain undefined.
Eccentricity[edit | edit source]
The eccentricity e can be determined from the magnitude of the eccentricity vector:
[eccentricity vector]
Alternately, it can be expressed as:
[eccentricity]
though the eccentricity vector will be needed in the calculation of later elements.
Inclination ()[edit | edit source]
The inclination, i is the angle between the K unit vector and the angular momentum vector h. It can be calculated using:
[Orbital Inclination]
The angle of inclination is always less than 180°.
Longitude of the Ascending Node ()[edit | edit source]
The longitude of the ascending node, Ω, is the angle between the ascending node and the I unit vector. It can be calculated as:
[Longitude of the Ascending Node]
If the nJ component is greater than zero, then Ω is less than 180°. Otherwise, Ω is greater than 180°.
Argument of Periapsis ()[edit | edit source]
The argument of periapsis is the angle in the orbital plane between the ascending node and the periapsis. We can calculate it as:
[Argument of Periapsis]
If eK is greater than 0, then ω is less than 180°. Otherwise, ω is greater than 180°.
Time of Periapsis Passage[edit | edit source]
The time of periapsis passage is the time when the satellite reaches periapsis. We define this time as Tp. It can be determined from observation. This is the sixth orbital parameter that allows calculating the position of a celestial object in any time.
Optional Elements[edit | edit source]
Longitude of Periapsis ()[edit | edit source]
Longitude of the Periapsis is the sum of the Longitude of the Ascending Node and the Argument of Perigee
[Longitude of Periapsis]
True Anomaly at Epoch ()[edit | edit source]
True anomaly at epoch is the angle from the periapsis point to the satellite's radius vector at epoch T0, and is denoted
Argument of Latitude at Epoch ()[edit | edit source]
Argument of Latitude at epoch is the angle between the ascending node and the satellite at epoch
True Longitude at Epoch ()[edit | edit source]
True longitude at epoch is the angle between the reference direction (usually the vernal equinox ♈) and the satellite's position. It is measured from the reference direction to the ascending node (if one exists) in the reference plane and then from the ascending node to the satellite's position in the plane of orbit.
Finding r and v[edit | edit source]
From the five classical orbital elements, we can determine r and v.
Where P and Q are unit vectors in the perifocal coordinate system. Using our coordinate transformations, we can convert these into geocentric-equatorial coordinates.


![{\displaystyle a=-{\frac {\mu }{2{\mathcal {E}}}}=-{\frac {\mu }{2}}\left[{\frac {v^{2}}{2}}-{\frac {\mu }{r}}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19de76e0d6d9f532d138a805a222b7a0d3e9105)
















![{\displaystyle \mathbf {v} ={\sqrt {\frac {\mu }{p}}}[-sin(\nu )\mathbf {P} +e\mathbf {Q} +\cos(\nu )\mathbf {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0967d59e38d152d5bfdf0facb16d1a49b86a4fa)