Artificial Intelligence/Search/Recommender Systems/Boltzmann Machines

This article describes using Boltzmann Machines for recommender systems.

What is a recommender system?

There is a bunch of users who may order (read, view, buy) bunch of items. Users give grades (or ratings) to items. Our task is to predict, as precise as possible, what grade a user would give to a new item, based on his and other user's previous ratings, in order to recommend items which he or she may like.

Most recommender system have following features:

• There are much more users than items
• All or almost all user rated only small fraction of items
• There is a small number of possible grades (often 1,2,3,4,5).
• There is a wide variance in number of rated items.

As Netflix Prize contest showed, there is no approach which is superior to others. For optimal results, several approaches should be combined together. One of them, Restricted Boltzmann Machines (RBM), is described here.

Notation

• U - set of users
• I - set of items
• G - set of grades
• $U_{i}$ - set of users who rated the item $i$.
• $I_{u}$ - set of items rated by user $u$.
• $G_{ui}$ - grade given by user $u$ to item $i$.
• ${\hat {G}}_{ui}$ - prediction for grade given by user $u$ to item $i$.
• T - training set. Each member of T is a triplet $(u,i,G_{ui})$.

SVD

Before describing RBM model, we briefly describe SVD model (Singular Value Decomposition) which is maybe the single best approach.

Under SVD, each user $u$ is represented by a feature vector $\mathbf {x} _{u}=(x_{u1},...,x_{uN})$, where N is the dimensionality of the model. Similarly, each item $i$ is represented by a feature vector $\mathbf {y} _{i}=(y_{i1},...,y_{iN})$.

The predicted grade is product of two vectors:

${\hat {G}}_{ui}=\mathbf {x} _{u}\mathbf {y} _{i}=\sum _{f=1}^{N}x_{uf}y_{if}$

Here x's and y's are parameters to be discovered by the model to fit the training set.

The model is intuitive, since features represent various qualities of the items. For example, when recommending movies, some feature may be highly positive for romantic movies, zero or negative for movies without any romantic appeal, and highly negative for cynical movies which ridicule romantics. The corresponding feature in user feature vectors will be negative for users who hate romantics, and positive in opposite case.

The simplest way to learn the model is to minimize the total error $E={1 \over 2}\sum _{(u,i,g)\in T}(\mathbf {x} _{u}\mathbf {y} _{i}-g)^{2}$. We can do it by gradient descend, cyclically presenting data from the training set, and for each $(u,i,g)$ changing parameters in the direction opposite to gradient of E:

$r_{ui}\leftarrow \mathbf {x} _{u}\mathbf {y} _{i}-g$

$\mathbf {x} _{u}\leftarrow \mathbf {x} _{u}-L\mathbf {y} _{i}r_{ui}$

$\mathbf {y} _{i}\leftarrow \mathbf {y} _{i}-L\mathbf {x} _{u}r_{ui}$

Here L is a learning parameter, which sets the overall speed of gradient descent.

However, for users and movies with few data, this approach tends to construct huge feature vectors, because this fits the data better. To prohibit this, and to utilize the knowledge that big feature values are improbable, relaxation term should be added:

$\mathbf {x} _{u}\leftarrow \mathbf {x} _{u}-L(\mathbf {y} _{i}r_{ui}-K\mathbf {x} _{u})$

$\mathbf {y} _{i}\leftarrow \mathbf {y} _{i}-L(\mathbf {x} _{u}r_{ui}-K\mathbf {y} _{i})$

For more detailed explanation of SVD, see Simon Funk's "Netflix Update: Try This at Home" [1]. However, his algorithm adds one feature at a time, which later was found not as good as learning all features simultaneously.

RBM

Now we get to the Boltzmann Machine model.

As a first step, suppose that instead of grade, we can predict probability for a specific grade:

$p_{uig}=$ probability that $G_{ui}=g$.

We can do it with approach similar to one described in the previous section:

$p_{uig}=\mathbf {x} _{u}\mathbf {y} _{ig}$

(Why not $\mathbf {x} _{ug}\mathbf {y} _{i}$? Because usually there are much more users than items, therefore $\mathbf {x} _{ug}$'s would contain huge number of parameters.)

But we can do better than this. Firstly, we can use the fact that the total probability for all grades is 1:

$p_{uig}={\frac {\mathbf {x} _{u}\mathbf {y} _{ig}}{\sum _{g}\mathbf {x} _{u}\mathbf {y} _{ig}}}$

Secondly, since probabilities are always from 0 to 1, they are better described not by vector product itself, but by logistic function of it:

Logistic function

$p_{uig}={\frac {f(\mathbf {x} _{u}\mathbf {y} _{ig})}{\sum _{g}f(\mathbf {x} _{u}\mathbf {y} _{ig})}}$

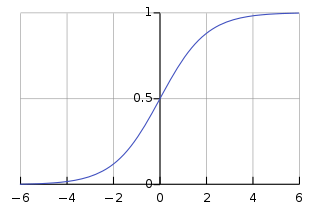
where logistic function f is defined as:

$f(x)={1 \over 1+e^{-x}}$

Redefining $\mathbf {y} _{ig}$ as weights W and $\mathbf {x} _{u}$ as hidden units, and requesting that all x's will be 0 or 1, we get:

$p_{uig}={\frac {f(\mathbf {x} _{u}\mathbf {W} _{ig})}{\sum _{g}f(\mathbf {x} _{u}\mathbf {W} _{ig})}}$

which is the Boltzmann Machine model.