A-level Chemistry/AQA/Module 1/Atomic Structure

The Atom

The Greek Philosopher Democritus believed that all matter was made up of small indivisible parts, which he called atoms. The word atom comes from the Greek a, meaning not, or without, and tom, meaning to cut. Therefore, the word atom means: not cuttable. He theorised that if one cut a piece of cheese in half, then in half again, and again, and again, et cetera, one would be left with a piece too small to subdivide. This was his single atom.

We now know that an atom is the smallest part of something that retains its identity, although the atom itself can be subdivided. In other words, once we begin to look inside the atom, we can no longer tell which element the atom is.

The atom itself comprises a central nucleus, in which most of the mass is concentrated, with electrons orbiting around the outside of this nucleus. This central nucleus consists of protons and neutrons. The properties of these three kinds of particle are given in the following table.

Particle	Relative Charge	Relative Mass	Absolute Charge	Absolute Mass
Proton	+1	1	$1.60\times 10^{-19}$	$1.67\times 10^{-27}$
Neutron	0	1	0	$1.67\times 10^{-27}$
Electron	-1	0 (Negligible, or approximately ${\frac {1}{1800}}$)	$-1.60\times 10^{-19}$	$9.11\times 10^{-31}$

In the neutral, or elemental atom there are equal numbers of protons and electrons. This causes the atom to have no overall charge.

Atomic Number and Mass Number

There are two useful pieces of information that we can glean from the nucleus of an atom. The first is its atomic number. This allows us to identify which element an atom is. The atomic number, usually denoted by the letter Z, is the number of protons in the nucleus of an atom. It is this which places an element in the periodic table.

The second is the mass number. This is equal to the number of protons, plus the number of neutrons (remember that electrons have negligible mass). It is given the symbol A.The number of neutrons in an atom, therefore, is equal to the mass number (A), minus the atomic number (Z)

Isotopes

Sometimes an atom's proton number will show that it is a particular element, and yet its mass number will be different to other atoms of that element. Atoms which have the same proton number, yet different mass numbers, are referred to as isotopes of the element. The difference in mass number is caused by the presence of extra, or fewer neutrons in the nucleus.

Since the number of protons (and, therefore, of electrons) is the same, the chemical properties of these materials are the same as those of the standard element. The physical properties (melting/boiling point etc.) DO change.

We usually refer to isotopes by the element name, followed by the mass number. For example, a carbon atom with a mass number of 12 (six protons, and six neutrons) is known as carbon-12. This is represented thus: ${}_{6}^{12}\!C$

One of the most useful isotopes is carbon-14. This is the atom ${}_{6}^{14}\!C$. It is radioactive, and can be used to determine the age of organic material as old as 60,000 years! Other isotopes are used in medicine as tracers, to determine the location of any blockages in the body.

Mass Spectroscopy

Mass Spectroscopy is a technique used to determine the relative abundance of various isotopes within a sample. It can be broken down into four stages.

1. Vaporisation and Ionisation The sample to be analysed is introduced into a vacuum chamber. The sample is vaporised. This is essential if the following stages are to succeed. The vacuum is very important, since the electrons which are to be fired at the sample must have a "clear run", so to speak. If they were not in a vacuum they would collide with air molecules.

The sample is now ionised. For this, an electron gun is used. This is, in essence, a device which fires high energy electrons into the sample. These electrons knock electrons in the sample out of orbit, ionising it. Particles in the sample are now positively charged, as shown below.

$X_{(g)}\to X_{(g)}^{+}+e_{(g)}^{-}$

$He_{(g)}\to He_{(g)}^{+}+e_{(g)}^{-}$

These two equations show the first ionisation stage. It is possible, however, for an ion to become ionised by a second electron. This is unlikely, since the second ionisation is much higher than the first, and unlikely to be reached. This rare event is represented by this equation:

$X_{(g)}^{+}\to X_{(g)}^{2+}+e_{(g)}^{-}$

2. Acceleration

Since opposite electrical charges attract, we can move the particles using an electric field. The particles are positively charged (electrons have been removed) so we use negatively charged electrical plates to accelerate the particles down the machine.

3. Deflection

We now use an electromagnet to deflect the particles. As the particles accelerate through the magnetic field, they change direction. Particles with large mass-to-charge (m/z) ratios are deflected by small amounts, whereas particles with smaller mass-to-charge ratios are deflected by larger amounts. This separarates ions of different mass-to-charge ratios.

4. Detection

The various species in the sample are now separated. The particles accelerate into a detector plate. Since they are charged, upon hitting the plate a small electrical current is produced. This current is recorded. The relative strength of the magnetic field at the time of detection can be used to calculate the m/z value of the ions detected. This allows us to determine the constituent ions of the sample. It is not possible, however, to distinguish between ions of the same m/z value, since they will be equally deflected!

This page gives more information on mass spectroscopy: http://www.chemguide.co.uk/analysis/masspec/howitworks.html#top.

Relative Masses

The following two definitions are required to be learnt for module one, although they may appear esoteric at first.

Relative Atomic Mass ($A_{r}$)

$A_{r}={\frac {{\mbox{Mean Mass of One Atom}}\times 12}{{\mbox{Mass of One Atom of }}{}_{6}^{12}\!C}}$

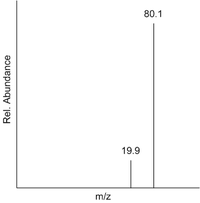
This can be calculated from the mass spectrum of a sample by multiplying each peak's m/z value by its relative abundance. This sum is then divided by the total relative abundance. This is shown below for the mass spectrum of boron, in which the two peaks represent ${}^{10}\!B$ and ${}^{11}\!B$ respectively.

${\frac {(19.9\times 10)+(80.1\times 11)}{100}}=10.8$

This can also be calculated from data in a table, as shown in this example for lead.

m/z	Relative Abundance
204	1.55
206	23.6
207	22.6
208	52.3

(It is important to note here that the relative abundances add up to 100.05, NOT 100.)

${\frac {(1.55\times 204)+(23.6\times 206)+(22.6\times 207)+(52.3\times 208)}{100.05}}=207.24$

Relative Molecular Mass ($M_{r}$)

$M_{r}={\frac {{\mbox{Mean Mass of One Molecule}}\times 12}{{\mbox{Mass of One Atom of }}{}_{6}^{12}\!C}}$

This can be calculated from a mass spectrum by taking the m/z value of the peak furthest to the right of the graph, as shown in this example for ammonia.

Electronic Configuration

At GCSE level, electrons are presented as point like entities that orbit around the nucleus of the atom, with the first orbital being able to hold two electrons, the second eight, and the third eighteen. We now know that this is not strictly accurate, and at A level a more sophisticated model is required.

We think of the electron orbitals as inhabiting a sub-level within a principal level. Each sub-level is capable of containing orbitals of a single shape referenced by the letters s,p,d and f. The sub levels themselves are commonly referred to by the letter of the orbital type which they can contain. Instead of saying the 3rd sub level of principal level 4 you would say the d sub level of level 4.

In the table below you should be able to see that the third sub level (d) of principal level 3 can contain 5 orbitals of type d. As each orbital can contain up to 2 electrons this means that this sub level can contain 10 electrons.

Principal Level	Sub-level	Electrons
n=1	→ 1 type s orbital	2
Maximum Electrons in level		2
n=2	→ 1 type s orbital	2
	→ 3 type p orbitals	6
Maximum Electrons in level		8
n=3	→ 1 type s orbital	2
	→ 3 type p orbitals	6
	→ 5 type d orbitals	10
Maximum Electrons in level		18
n=4	→ 1 type s orbital	2
	→ 3 type p orbitals	6
	→ 5 type d orbitals	10
	→ 7 type f orbitals	14
Maximum Electrons in level		32

As shown in the table, the maximum number of orbitals in each type of sub level is related to its type. An 's' sub level can contain only one orbital (2 electrons), a 'p' sub level con contain a maximum of 3 orbitals (6 electrons) ; a 'd' a maximum of 5 orbitals (10 electrons); and an 'f' a maximum of 7 (14 electrons).

The capacity of each principal level is the sum of the capacities of its sub levels. You should be able to see that the capacities of the principal levels equate to the more simple GCSE model of electron shells.

There are certain rules that it is necessary to know about the filling of these orbitals.

1. The orbitals are filled in the order of the table, from top to bottom. This is in ascending order of energy; that is to say, each successive energy level (lower down the table) has higher energy than the previous level.
2. Each orbital must be filled before electrons are put into the next orbital. An atom, for example, must always have two electrons in its 1s sub-energy level before any are placed into the 2s orbital.

For AQA A level chemistry you are required to be able to fill energy level diagrams to level 4s.