Waves/Thin Films
Thin Films
[edit | edit source]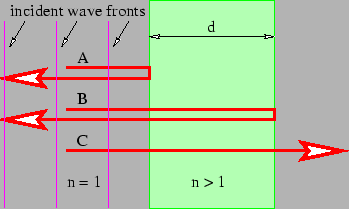
Figure 1.14: Plane light wave normally incident on a transparent thin film of thickness and index of refraction . Partial reflection occurs at the front surface of the film, resulting in beam A, and at the rear surface, resulting in beam B. Much of the wave passes completely through the film, as with C.
One of the most revealing examples of interference occurs when light interacts with a thin film of transparent material such as a soap bubble. Figure 1.14 shows how a plane wave normally incident on the film is partially reflected by the front and rear surfaces. The waves reflected off the front and rear surfaces of the film interfere with each other. The interference can be either constructive or destructive depending on the phase difference between the two reflected waves.
If the wavelength of the incoming wave is , one would naively expect constructive interference to occur between the A and B beams if were an integral multiple of .
Two factors complicate this picture. First, the wavelength inside the film is not , but , where is the index of refraction of the film. Constructive interference would then occur if . Second, it turns out that an additional phase shift of half a wavelength occurs upon reflection when the wave is incident on material with a higher index of refraction than the medium in which the incident beam is immersed. This phase shift doesn't occur when light is reflected from a region with lower index of refraction than felt by the incident beam. Thus beam B doesn't acquire any additional phase shift upon reflection. As a consequence, constructive interference actually occurs when
- (2.23)
while destructive interference results when
- (2.24)
When we look at a soap bubble, we see bands of colors reflected back from a light source. What is the origin of these bands? Light from ordinary sources is generally a mixture of wavelengths ranging from roughly (violet light) to (red light). In between violet and red we also have blue, green, and yellow light, in that order. Because of the different wavelengths associated with different colors, it is clear that for a mixed light source we will have some colors interfering constructively while others interfere destructively. Those undergoing constructive interference will be visible in reflection, while those undergoing destructive interference will not.
Another factor enters as well. If the light is not normally incident on the film, the difference in the distances traveled between beams reflected off of the front and rear faces of the film will not be just twice the thickness of the film. To understand this case quantitatively, we need the concept of refraction, which will be developed later in the context of geometrical optics. However, it should be clear that different wavelengths will undergo constructive interference for different angles of incidence of the incoming light. Different portions of the thin film will in general be viewed at different angles, and will therefore exhibit different colors under reflection, resulting in the colorful patterns normally seen in soap bubbles.










