Waves/Fermat's Principle
Fermat's Principle
[edit | edit source]An alternate approach to geometrical optics can be developed from Fermat's principle. This principle states (in its simplest form) that light waves of a given frequency traverse the path between two points which takes the least time. The most obvious example of this is the passage of light through a homogeneous medium in which the speed of light doesn't change with position. In this case shortest time is equivalent to the shortest distance between the points, which, as we all know, is a straight line. Thus, Fermat's principle is consistent with light traveling in a straight line in a homogeneous medium.

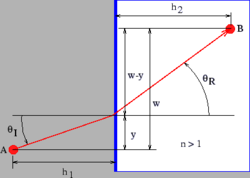
Fermat's principle can also be used to derive the laws of reflection and refraction. For instance, figure 3.10 shows a candidate ray for reflection in which the angles of incidence and reflection are not equal. The time required for the light to go from point A to point B is
- (4.12)
where is the speed of light. We find the minimum time by differentiating with respect to and setting the result to zero, with the result that
- (4.13)
However, we note that the left side of this equation is simply , while the right side is , so that the minimum time condition reduces to or , which is the law of reflection.

A similar analysis may be done to derive Snell's law of refraction. The speed of light in a medium with refractive index is , where is its speed in a vacuum. Thus, the time required for light to go some distance in such a medium is times the time light takes to go the same distance in a vacuum. Referring to figure 3.11, the time required for light to go from A to B becomes
- (4.14)
This results in the condition
- (4.15)
where is now the refracted angle. We recognize this result as Snell's law.
Notice that the reflection case illustrates a point about Fermat's principle: The minimum time may actually be a local rather than a global minimum -- after all, in figure 3.10, the global minimum distance from A to B is still just a straight line between the two points! In fact, light starting from point A will reach point B by both routes -- the direct route and the reflected route.
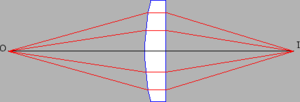
Figure 3.13 illustrates a rather peculiar situation. Notice that all the rays from point O which intercept the lens end up at point I. This would seem to contradict Fermat's principle, in that only the minimum (or maximum) time trajectories should occur. However, a calculation shows that all the illustrated trajectories in this particular case take the same time. Thus, the light cannot choose one trajectory over another using Fermat's principle and all of the trajectories are equally favored. Note that this inference applies not to just any set of trajectories, but only those going from one focal point to another.



![{\displaystyle t=[\{h_{1}^{2}+y^{2}\}^{1/2}+\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df17016aefc93a260a7cb54238dadba5348bbf74)










![{\displaystyle t=[\{h_{1}^{2}+y^{2}\}^{1/2}+n\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dffa4fe43759604e610459d5af24cae25ad3891c)
