Using an Abacus/Modern division
Introduction and first methods
[edit | edit source]Euclidean division
[edit | edit source]If we consider two natural numbers and , the division of by (indicated as or ) answers the question of how many times the number is contained in number . Number in is called the dividend and the divisor. The answer is called the quotient.
Let's take and as an example. There is no simpler way to proceed to answer the question than by repeated subtraction counting the number of times we subtract the divisor from the dividend. We can do it directly on the abacus using a column as counter:
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKL | |
| 35 1225 | |
| +1 -35 | subtract 35 from KL, add 1 to counter F |
| 35 1 1190 | |
| +1 -35 | subtract 35 from KL, add 1 to counter F |
| 35 2 1155 | |
| +1 -35 | subtract 35 from KL, add 1 to counter F |
| 35 3 1120 | |
| ... | Continue 33 times more... |
| 35 33 70 | |
| +1 -35 | subtract 35 from KL, add 1 to counter F |
| 35 34 35 | |
| +1 -35 | subtract 35 from KL, add 1 to counter F |
| 35 35 00 | Done, quotient is 35 in EF! |
Thus we discover that the number is contained exactly times in , since we cannot continue to subtract without starting to deal with negative numbers. Therefore, in this example, the quotient is: .
As we can see, in this case we can write or
which we cannot expect in the general case. If we repeat the process with , we would see that after subtracting times we would have left on the abacus, from which we cannot continue subtracting without entering negative numbers. Therefore we have that ; that is, the result of dividing by is a quotient of leaving a remainder of . In general we will have:
where:
- : dividend
- : divisor
- : quotient
- : remainder
In the case that the remainder is zero, the dividend is a multiple of the divisor.
This is the concept of Euclidian division for natural numbers to which the division of numbers with decimal fractions can be reduced.
Some improvements: Chunking methods
[edit | edit source]The procedure followed in the previous section is the simplest possible conceptually, but it is extraordinarily long and inefficient. Instead of starting directly by subtracting the divisor () from the dividend, let's start by asking what power of 10 times the divisor we can subtract from the dividend; in our case: can we subtract 3500, 350, or only 35? Clearly we can subtract 350 and we will start subtracting 350 chunks, and when we cannot continue, we will start subtracting 35 chunks as follows:
| Abacus | Comment |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Start, counter in D, |
| 35 1 875 | subtract 35 from GH, add 1 to counter D, |
| 35 2 525 | subtract 35 from GH, add 1 to counter D, |
| 35 3 175 | subtract 35 from GH, add 1 to counter D, |
| 35 31140 | subtract 35 from HI, add 1 to counter E, |
| 35 32105 | subtract 35 from HI, add 1 to counter E, |
| 35 33 70 | subtract 35 from HI, add 1 to counter E, |
| 35 34 35 | subtract 35 from HI, add 1 to counter E, |
| 35 35 00 | subtract 35 from HI, add 1 to counter E. |
| 35 35 | No remainder. Done, quotient is 35! |
Which has been a lot faster (We have intentionally reduced the distance between the counter and the dividend as much as possible. This obscures the process somewhat but brings us closer to what we will routinely do with the modern division method. Please study the above calculation carefully using your own abacus). Let's continue from here looking for even more efficiency.
If we can easily double the divisor and retain it in memory, we can shorten the operation by subtracting one or two times the divisor chunks.
| times | chunks |
|---|---|
| 1 | 35 |
| 2 | 70 |
| Abacus | Comment |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Start, counter in D, |
| 35 2 525 | subtract 70 from GH, add 2 to counter D, |
| 35 3 175 | subtract 35 from GH, add 1 to counter D, |
| 35 32105 | subtract 70 from HI, add 2 to counter E, |
| 35 34 35 | subtract 70 from HI, add 2 to counter E, |
| 35 35 00 | subtract 35 from HI, add 1 to counter E. |
| 35 35 | No remainder. Done, quotient is 35! |
Or even better if we can build a table like the one below by doubling the divisor three times[1]:
| times | chunks |
|---|---|
| 1 | 35 |
| 2 | 70 |
| 4 | 140 |
| 8 | 280 |
| Abacus | Comment |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Start, counter in D, |
| 35 2 525 | subtract 70 from GH, add 2 to counter D, |
| 35 3 175 | subtract 35 from GH, add 1 to counter D, |
| 35 34 35 | subtract 140 from HI, add 4 to counter E, |
| 35 35 00 | subtract 35 from HI, add 1 to counter E. |
| 35 35 | No remainder. Done, quotient is 35! |
which is somewhat shorter and, clearly, nothing could be faster than having a complete multiplication table of the divisor
Multiplication table
[edit | edit source]| times | chunks |
|---|---|
| 1 | 35 |
| 2 | 70 |
| 3 | 105 |
| 4 | 140 |
| 5 | 175 |
| 6 | 210 |
| 7 | 245 |
| 8 | 280 |
| 9 | 315 |
then
| Abacus | Comment |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Start, counter in D, |
| 35 3 175 | subtract 105 from GH, add 3 to counter D, |
| 35 35 00 | subtract 175 from HI, add 5 to counter E. |
| 35 35 | No remainder. Done, quotient is 35! |
There is no doubt, this is an optimal division method, nothing can be faster and more comfortable ... once we have a chunk table like the one above. But calculating the chunk table is time consuming and requires paper and pencil to write it and this extra work would only be justified if we have a large number of divisions to do with the same common divisor.
In 1617 John Napier, the father of logarithms, presented his invention to alleviate this problem consisting of a series of rods, known as Napier's Bones, with the one-digit multiplication table written on them and that could be combined to get the multiplication table of any number. For example, in our case

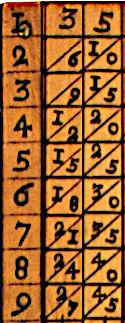
|
1 | 35 |
| 2 | 70 | |
| 3 | 105 | |
| 4 | 140 | |
| 5 | 175 | |
| 6 | 210 | |
| 7 | 245 | |
| 8 | 280 | |
| 9 | 315 |
There is no doubt that such an invention spread to the East and was used in conjunction with the abacus, but this use must be considered as exceptional; not everyone had Napier bones close at hand. Another tool is needed and that tool is the traditional 1-digit multiplication table that is learned by heart and that we are going to use as an approximation to the specific multiplication table of the divisor (the one used above), this table will guide us to choose the digit of the quotient that we must try.
It should be noted that the above procedures do not exhaust the possibilities of the chunking methods. If you read The Definitive Higher Math Guide on Integer Long Division[2] article, you will be amazed at the variety of division methods that can be performed.
Modern Division
[edit | edit source]Modern vs. traditional division
[edit | edit source]The modern method of division is so called because throughout the first half of the 20th century its use has displaced that of the traditional method, but in fact it is much older than this, having been displaced by it in the 13th century. A characteristic of the modern method is the use of the 1-digit multiplication table both as a guide to the choice of the interim quotient figure that we have to try and for the calculation of the chunk that we have to subtract from the dividend.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
By comparison, the traditional method uses both a special division table as a guide for the interim quotient figure and the multiplication table for calculating the chunk to subtract.
The main reason why the modern method began to displace the traditional method in Japan after the Meiji Restoration is that it can be learned more easily and quickly by those who already know how to divide with paper and pencil, since it does not require memorization of the complex division table. On the other hand, the traditional method makes the division a completely automated process, without the need to think, one only has to follow the rules to obtain the result, which allows the operation to be carried out without any mental fatigue. If you are interested in this topic you can consult the Wikibook: Traditional Abacus and Bead Arithmetic.
Key point of division with the abacus
[edit | edit source]One of the key points of learning abacus is to be aware that this instrument allows us to correct some things very quickly and without leaving traces, which makes the abacus an instrument especially suited to trial and error procedures. This is specially useful in the case of division. So, if we have to divide 634263÷79283, instead of busting our brain trying to find the correct quotient figure, we simply choose an approximate provisional or interim figure by simplifying the original problem to 63÷7 and test it by trying to subtract the chunk (interim quotient digit)✕79283 from the dividend; one of the following will occur:
- The interim quotient digit is correct
- that is, we can subtract the chunk (interim quotient digit) ✕ (divisor) without entering negative numbers but we cannot subtract the quotient one more time because the remainder is less than the divisor.
- It is insufficient and we must revise it up
- we can subtract the chunk (interim quotient digit) ✕ (divisor) without entering negative numbers but we can still subtract the quotient one more time because the remainder is greater/equal than the divisor. We add one to the interim quotient and subtract the divisor again from the remainder.
- It is excessive and we must revise it down
- this is the most complex and error-prone situation. We usually discover too late (in the middle of the chunk subtraction) that the interim figure is excessive and we need to go back, subtract one from the quotient, and restore the dividend/remainder by adding what has been subtracted in excess before we can continue.
Therefore, the process of obtaining a digit of the quotient has two phases:
- Choose an interim quotient digit.
- Test if it is correct and modify it if not.
Once we have found the correct figure, we will generally have a non-zero remainder that will act as a dividend if we want to extend the division to the next digit of the quotient.
We will see all of this throughout the examples that follow, but first, we need a few words about how to organize the division on the abacus.
Modern division arrangement
[edit | edit source]The dividend is the active term with which we are going to work in the abacus, the divisor is inactive and remains unchanged during the operation, in fact it is not essential to enter it in the abacus but it is recommended, especially for beginners. As in the case of multiplication, there are two styles to place dividend and divisor on the abacus, each with its advantages and disadvantages.
Traditional Chinese arrangement
[edit | edit source]The divisor goes to the far right of the abacus while the dividend is to the left, leaving at least two columns free to its left.
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 5 | 3 | 5 |
Traditional Japanese arrangement
[edit | edit source]The divisor goes to the extreme left of the abacus while the dividend is to its right, leaving at least four free columns between the two terms.
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 1 | 2 | 2 | 5 |
In this book we will use the Japanese style for the examples, but feel free to try both.
Placing the quotient figure
[edit | edit source]The interim quotient figure is placed in one of the two columns directly to the left of the dividend. To decide which one we need to compare the divisor with an equal number of the first digits of the dividend, adding zeros to its right if necessary; call this the working dividend:
- Working dividend greater than or equal to the divisor
- this means that the divisor goes into the working dividend and the quotient, i.e. the number of times the divisor goes into the working dividend, is arranged in the second column to the left of the first digit of the dividend
- Example: 827÷46, 82, the working dividend, is greater than 46, then the interim quotient goes to the second column to the left of dividend. Multiplication table suggest us using 2 as interim quotient (simplify 827÷46 to 8÷4)
827÷46 Abacus Comment ABCDEFGHIJKLM 46 827 46 2 827 Place interim quotient 2 in E
- Working dividend smaller than the divisor
- this means that the divisor does not go into the working dividend. In this case, we need to include the next digit of the dividend, or a zero if there are no more left, in our working dividend, and the quotient, the number of times the divisor goes into this expanded working dividend, is arranged in the column directly to the left of the first digit of the dividend
- Example: 18÷467, 180 is less than 467, then the working dividend is 1800 and the interim quotient goes to the first column to the left of dividend. Multiplication table suggest us using 4 as interim quotient after simplifying 1800÷467 to 18÷4.
Caption text Abacus Comment ABCDEFGHIJKLM 467 18 467 418 Place interim quotient 4 in G
Examples
[edit | edit source]You should start by doing exercises with single-digit divisors and later try divisors with two, three, etc. figures. With one-digit divisors you should never have to revise up or down. For example you can divide 123456789 by the digits 2, 3, ..., 9. Let's see the division by 9 here.
Example: 123456789÷9 = 13717421
[edit | edit source]- Please read the "->" symbol as: "the multiplication table suggests using ...".
- As you will see, in all cases except the last one, the working dividend is less than the divisor and we need to expand it to two digits.
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKLMNO | |
| 9 123456789 | 12/9 -> 1 as interim quotient |
| 9 1123456789 | place i. quotient in E |
| -9 | subtract 9✕1=9 from FG |
| 9 1 33456789 | 33/9 -> 3 as interim quotient |
| 9 1333456789 | place i. quotient in F |
| -27 | subtract 9✕3=27 from GH |
| 9 13 6456789 | 64/9 -> 7 as interim quotient |
| 9 1376456789 | place i. quotient in G |
| -63 | subtract 9✕7=63 from HI |
| 9 137 156789 | 15/9 -> 1 as interim quotient |
| 9 1371156789 | place i. quotient in H |
| -9 | subtract 9✕1=9 from IJ |
| 9 1371 66789 | 66/9 -> 7 as interim quotient |
| 9 1371766789 | place i. quotient in I |
| -63 | subtract 9✕7=63 from JK |
| 9 13717 3789 | 37/9 -> 4 as interim quotient |
| 9 1371743789 | place i. quotient in J |
| -36 | subtract 9✕4=36 from KL |
| 9 137174 189 | 18/9 -> 2 as interim quotient |
| 9 1371742189 | place i. quotient in K |
| -18 | subtract 9✕2=18 from LM |
| 9 1371742 9 | 9/9 -> 1 as interim quotient |
| 9 13717421 9 | place i. quotient in L |
| -9 | subtract 9✕1=9 from MN |
| 9 13717421 | No remainder! Done
123456789÷9 = 13717421 |
123456789 is a curious number, it is precisely the product of 9 by 13717421, a large prime!
Example: 1225÷35 = 35 Two-digit divisor. Revising down and up
[edit | edit source]| Abacus | Comment |
|---|---|
| ABCDEFGHIJ | |
| 35 1225 | 12÷3↦4 as interim quotient |
| +4 | enter interim quotient in F |
| 35 41225 | Now try to subtract the chunk 4✕35 from GHI, |
| -12 | first 4✕3 from GH |
| 35 40025 | then 4✕5 from HI |
| -20 | Cannot subtract! |
| -1 | Revise down interim quotient digit |
| 35 30025 | |
| +3 | return the excess subtracted from GHa |
| 35 30325 | |
| -15 | continue normally, subtract 3✕5 from HI |
| 35 3 175 | 17÷3↦5 as interim quotient |
| +5 | enter interim quotient in G |
| 35 35175 | Try to subtract chunk 5✕35 from HIJ |
| -15 | first 5✕3 from HI |
| 35 35025 | |
| -25 | then 5✕5 from IJ |
| 35 35 | No remainder, done! 1225÷35 = 35 |
Note:^a We have subtracted 4 × 3 = 12 from FGH, but if the correct quotient digit is 3, we should have subtracted 3 × 3 = 9, so we subtracted 3 in excess (just the first digit of the divisor). We must return this excess before continuing.
Now, suppose that after our "bad experience" revising down the first figure of the quotient, and in an excess of prudence, we choose 4 as as the second interim quotient instead of 5 as suggested by the multiplication table. Then we continue this way:
| Abacus | Comment |
|---|---|
| ABCDEFGHI | |
| 35 3 175 | 17÷3 -> 5, but we use 4! |
| +4 | enter interim quotient in G |
| 35 34175 | Try to subtract chunk 4✕35 from HIJ |
| -12 | first 4✕3 = 12 from HI |
| -20 | then 4✕5 = 20 from IJ |
| 35 34 35 | remainder greater or equal to divisor! |
| +1 | revise up G |
| -35 | subtract divisor from remainder HI |
| 35 35 | No remainder, Done! |
Example 1÷327
[edit | edit source]So far we have considered divisions between natural numbers with quotients and remainders as well as natural numbers, but we can operate with decimal numbers exactly as we do in written calculation with long division. For example, let's find the inverse of 327; that is, 1/327 in an abacus with 13 columns.
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKLM | |
| 327 1 | 10/3 -> 3 as interim quotient |
| 327 31 | enter interim quotient in G |
| -09 | subtract 3✕3=9 from HI |
| 327 3 1 | |
| -06 | subtract 3✕2=6 from IJ |
| 327 3 4 | |
| -21 | subtract 3✕7=21 from JK |
| 327 3 19 | 19/3 -> 6 as interim quotient |
| 327 30619 | enter interim quotient in I |
| -18 | subtract 6✕3=18 from JK |
| 327 306 1 | |
| -12 | cannot subtract 6✕2=12 from KL! |
| -1 | revise down I |
| +3 | return the excess subtracted from JK |
| 327 305 4 | |
| -10 | continue normally, subtract 5✕2=10 from KL |
| 327 305 30 | |
| -35 | subtract 5✕7=35 from LM |
| 327 305 265 | 36/3 -> 8 as interim quotient |
| 327 3058265 | enter interim quotient in J |
| -24 | subtract 8✕3=24 from KL |
| 327 3058 25 | |
| -16 | subtract 8✕2=16 from LM |
| 327 3058 9 | cannot continue! Result: 3058 |
We have obtained as the first digits of , but so our result is actually . See below the rule to find the unit rod of the division.
Example: 634263÷79283 = 7,999987..., a tricky case
[edit | edit source]Finally let's get the first digit of the quotient of this especially malicious division
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKLM | |
| 79283 634263 | 63/7 -> try 9 |
| 79283 9634263 | |
| -63 | subtract 9*7=63 from HI |
| 79283 9004263 | |
| -81 | cannot subtract 9*9=81 from IJ! |
| -1 | revise D down |
| +7 | restore excess subtracted from remainder |
| 79283 8 74263 | |
| -72 | continue subtracting 8x9=72 from IJ |
| 79283 8 02263 | |
| -16 | subtract 8*2=16 from JK |
| 79283 8 00663 | |
| -64 | subtract 8*8=64 from KL |
| 79283 8 00023 | cannot subtract 8*3=24 from LM! |
| -1 | revise D down |
| +7928 | restore excess subtracted from remainder |
| 79283 7 79303 | |
| -21 | continue subtracting 7x3=21 from LM |
| 79283 7 79282 | quotient: 7, remainder: 79282 |
There is no doubt that in this case rounding the divisor 79283 to 80000 would have given us better results since 63÷/8 suggests using 7 (the correct figure) as the interim quotient digit.
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKLM | |
| 79283 634263 | 63/8 -> try 7 |
| 7634263 | |
| -49 | subtract 7*7=49 from HI |
| 79283 7144263 | |
| -63 | subtract 7*9=63 from IJ |
| 79283 7 81263 | |
| -14 | subtract 7*2=14 from JK |
| 79283 7 79863 | |
| -56 | subtract 7*8=56 from KL |
| 79283 7 79303 | |
| -21 | subtract 7*3=21 from LM |
| 79283 7 79282 | quotient: 7, remainder: 79282 |
The unit rod and decimals
[edit | edit source]The counterpart of the rule to find the unit rod of multiplication is the following rule for division:
The following table shows the values for some divisors:
| Multiplier | n |
|---|---|
| 32.7 | 2 |
| 3.27 | 1 |
| 0.327 | 0 |
| 0.00327 | -2 |
Example: 1/327 (we have seen it above)
| Abacus | Comment |
|---|---|
| ABCDEFGHIJKLM | |
| 327 1 | divisor has 3 digits. n=3 |
| . | dividend unit rod |
| ... | |
| 327 3058 9 | End of division. Result: 3058 |
| . | dividend unit rod |
| <--- | shift it n+1 = 4 positions to the left |
| . | unit rod of quotient |
| 3058 | so that this... |
| .003058 | ... should be read 0.003058 |
Multiplication and division as inverse operations
[edit | edit source]In written calculations we can always review our calculation to make sure that we have not made mistakes and that the result obtained is correct. In calculations with the abacus this is not possible since the abacus does not keep memory of the past and of intermediate results. We can resort to some sanity tests such as casting nines or elevens out, but the traditional way of checking the results with the abacus has been either to repeat the calculations or to undo the calculations.
Undoing additions and subtractions is as simple as starting from the result and subtracting what we have added, adding what we have subtracted; If we do both the calculation and the verification correctly, we should end up with a reset abacus. To verify a multiplication we will use division and, reciprocally, to verify a division we will use multiplication, adding the remainder if there is one. After doing this we will return the abacus to its starting state with the two original operands in their initial positions. Let's see an example:
| Abacus | Comment |
|---|---|
| ABCDEFGHIJ | |
| 64 2461 | 24/6 -> 4 as interim quotient |
| 42461 | enter interim quotient in F |
| -24 | subtract 4✕6=24 from GH |
| 64 4 61 | |
| -16 | cannot subtract 4✕4=16 from HI |
| -1 | revise down interim quotient digit |
| 64 3 61 | |
| +6 | return the excess subtracted from GH |
| 64 3 661 | |
| -12 | continue normally, subtract 3✕4=12 from HI |
| 64 3 541 | 54/6 -> 9, but we will use 8 |
| 64 38541 | |
| -48 | subtract 8✕6=48 from HI |
| 64 38 61 | |
| -32 | subtract 8✕4=32 from IJ |
| 64 38 29 | quotient: 38, remainder 29 |
| revision by multiplication start here! | |
| +48 | add 8✕6=48 to HI |
| 64 38509 | |
| +32 | add 8✕4=32 to IJ |
| 64 38541 | |
| 64 3 541 | clear G |
| +18 | add 3✕6=18 to GH |
| 64 32341 | |
| +12 | add 3✕4=12 to HI |
| 64 32461 | |
| 64 2461 | clear F. Initial status! |
It has been suggested in this book to use the number 123456789 for your first exercises in both multiplication and division by a single digit. Try combining them with the reverse operation; for example: divide 123456789 by 9 to get 13717421 and multiply this result by 9 to get 123456789 back to the same starting position on the abacus. Or start by multiplying 123456789 by 9 to get 1111111101 and then divide by 9 to get back to where you started. Try all the digits from 2 to 9.
References
[edit | edit source]- ↑ Wilson, Jeff. "Long Division Teaching Aid, "Double Division"". Double Division. Archived from the original on March 02, 2021.
{{cite web}}: Check date values in:|archivedate=(help); Text "year 2005" ignored (help); Unknown parameter|accesdate=ignored (|access-date=suggested) (help) - ↑ "The Definitive Higher Math Guide on Integer Long Division (and Its Variants)". Math Vault. Archived from the original on May 14, 2021.
{{cite web}}: Unknown parameter|accesdate=ignored (|access-date=suggested) (help); Unknown parameter|name=ignored (help)
External resources
[edit | edit source]Exercise sheets
- "The generator". Practicing the soroban.
{{cite web}}: Unknown parameter|accesdate=ignored (|access-date=suggested) (help)
Further reading
[edit | edit source]- Kojima, Takashi (1954), "Division", The Japanese Abacus: its Use and Theory, Tokyo: Charles E. Tuttle Co., Inc., ISBN 978-0-8048-0278-9
- Heffelfinger, Totton (2004). "Division". 算盤 Abacus: Mystery of the Bead. Archived from the original on June 29, 2021.
{{cite web}}: Unknown parameter|accesdate=ignored (|access-date=suggested) (help) - Siqueira, Edvaldo (2004). "Decimals & Division". 算盤 Abacus: Mystery of the Bead. Archived from the original on May 6, 2021.
{{cite web}}: Unknown parameter|accesdate=ignored (|access-date=suggested) (help)























