Using SPSS and PASW/Chi-Square
The Chi-Square test is used when trying to find a relationship between two nominal or ordinal variables. To reiterate, a nominal variable is one that is only measured by naming categories such as class, quality or kind. An ordinal variable is similar to a nominal variable, but the categories can be put in an order (e.g., ranked highest to lowest).
To calculate Chi-Square, we use a cross-tabulation, crosstab for short, which shows the frequencies of joint occurrences between two variables.
The hypothesis we will test in this chapter is whether or not there is a relationship between religious affiliation and belief in the afterlife. We will test this using an alpha of .05. To do a Chi-Square test in SPSS, complete the following steps:
You must have two nominal variables from a single sample that you can use to see if there is a relationship between them. For this example we will use religion (relig) and belief in the afterlife (postlife). For this example religion is the independent variable and belief in the afterlife is the dependent variable. This will be important later.
To run the test, select: Analyze → Descriptives → Crosstabs.
Once you click Crosstabs, a window will pop up where you will enter your chosen variables to be tested. Select the independent variable (relig) to go in the column and the dependent variable (postlife) to go in the row.
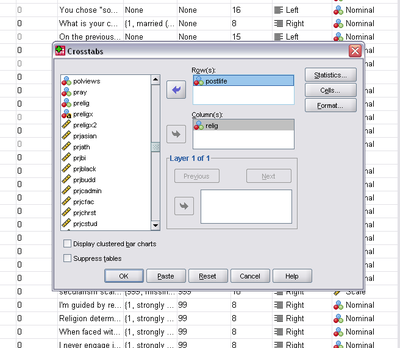
Next, click the statistics button and check the Chi-Square box.

Hit continue and then click on the cells button and check observed, expected and column percentages.

Then hit OK and an output window with the resulting cross-tabulation will pop up.
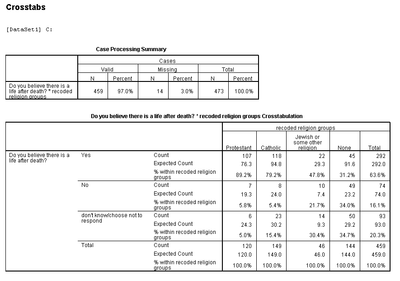
Next you must interpret the data. At the bottom of each column and end of every row there is a total for that specific group. The bottom right cell is the total number of cases in the sample. In each cell, it shows the observed joint occurrence between the two variables and the expected occurrence based on the totals that were observed. If there is NO relationship between the variables, the observed and expected frequencies will be the same. For our example, this is clearly not the case. They are different but we must look at the last box from our output window to see if our relationship is legitimate or if it was due to sampling error.

As we stated in the beginning, our alpha is .05. If the “Asymp. Sig. (2-sided)” for the Pearson Chi-Square statistic is less than .05, there is a relationship between the variables based on the level of confidence we stated in the beginning. As seen in the table below, the Chi-Square significance value is .000 which is less than our value of .05 which shows that there is a relationship between one’s religion and their belief in the afterlife.
Finally, we interpret the test in everyday terms, which also means we look more closely at the crosstab table as well. In the crosstab table it is clear that Protestants and Catholics are much more likely to report a belief in the afterlife than are Jews or Nones. Thus, we can say, “Jews and the non-religious are significantly less likely to believe in an afterlife than are Protestants and Catholics.” Do note that care must be taken in interpreting Chi-Square crosstabs as it is not always perfectly clear where the significant differences between scores lie.
Chapter contributed by Sarah Friswell.