Trigonometry/Introduction
Trigonometry is the study of the properties of triangles.
- "Tri" is Ancient Greek word for three,
- "gon" means angle,
- "metry" measurement
Together they make "measuring three angles of a triangle".
If you know some facts about a triangle, such as the lengths of its sides, then using trigonometry you can find out other facts about it. If you know the lengths of sides then you can find what the angles are. If you know the length of one side and of two of the angles, then you can work out what the remaining angle is, and also what the lengths of the other two sides are.
As a consequence the Ancient Greeks were able to use trigonometry to calculate the distance from the Earth to the Moon.
Starting to Learn Trigonometry
[edit | edit source]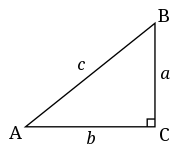
One of the first things we learn in trigonometry is how to calculate what the third angle in a triangle is when given the other two angles. For example, in a triangle if two of the angles are then the third angle must be too, since we know that they all need to add up to .
However, if we're instead told two lengths, say 7cm and 10cm, and if we're not told anything about the angles, then the third length has a range of possibilities, it could be anywhere between 0 and 17cm.
Solving in a Right Triangle
[edit | edit source]Remember, a right triangle has one angle that measures (a "right angle"). It's much simpler to calculate the missing third angle on a right triangle, so we will start by examining one, expect to see many more of them in the rest of this book.
In a right triangle we can work out the length of the longest side if given the lengths of the two shorter sides. In a right triangle the lengths of the sides have a particularly nice relationship to each other. The formula for this relationship is written:
The sides and are the ones that touch the angle and is the longer diagonal side that is across from it. You may sometimes see called the hypotenuse.
See Pythagoras' Theorem to start using this formula to calculate the length of that missing side.
Solving in Other Shapes
[edit | edit source]What if the triangle isn't a right-angled triangle, though?
More complex triangles can easily be divided into right triangles, so we learn about right-angled triangles enables us to work with other kinds of triangles too. Trigonometry and trigonometric functions can also be used with more complex shapes such as squares, hexagons, circles and ellipses. Ultimately the most important mathematical tools we have for measuring the universe are based on the study of the mathematics of triangles.
Trigonometry is a fundamental step in your mathematical education. From the seemingly simple shape, the right triangle, we gain tools and insight that help us in practical and theoretical endeavors. The subtle mathematical relationships between the right triangle, the circle, the sine wave, and the exponential curve can only be fully understood with a firm foundation in trigonometry.
Applications

Because many physical questions can be framed in terms of triangles, trigonometry has found wide use in the physical sciences and engineering.
Trigonometry is needed in surveying and architecture since relationships between lengths and angles in triangles are used directly.
Civil engineers, mechanical engineers, and physicists use trigonometry to understand how forces will be applied, and what direction different objects will move in when they push on or bump into each other.

Since trigonometric functions map to circles, and circles map to waves (we'll get to how all this works!), electrical engineers use trigonometry to make calculations about wavy patterns that they work with, such as AC power that comes out of your wall, or radio signals to your cell phone.
Computer graphics in movies and video games are actually millions of small triangles rendered on your screen, although there are a lot of little tricks that happen after that to make things look smooth and curvy.






