Trigonometry/Circles and Triangles/The Circumcircle
The circumcircle of a triangle is the unique circle passing through its three vertices.
The centre of the circumcircle is the circumcentre. It is the intersection of the perpendicular bisectors of the three sides. This can be explained as follows:
- Each bisector of a side is the locus of points equidistant from the two endpoints of the side, e.g. all the points on the bisector of are equidistant from point A and point B.
- On the bisector of points are equidistant from A and B. On the bisector of points are equidistant from B and C. The point where these two bisectors cross is both equidistant from A and B and equidistant from B and C. So the intersection point's distance from A is the same as its distance to B is the same as its distance to C. So it is equidistant from A and C and hence lies on the bisector of
- Where the three bisectors cross is equidistant from A,B and C. Hence a circle with centre that point can pass through all three points.
-
The circumcenter of an acute triangle is inside the triangle
-
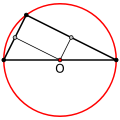
The circumcenter of a right triangle is on the hypotenuse
-
The circumcenter of an obtuse triangle is outside the triangle
The radius of this circle (the circumradius, usually denoted by R) is found as follows: if a is any side of the triangle and A is the angle opposite this side, . To prove this, consider a triangle where two of the sides are radii of the circumcircle and the third is the side of length a. This triangle is isosceles (since all radii are of equal length), and the angle between the radii is 2A since the angle at the centre of a circle is twice the angle at the circumference. The formula follows from applying simple trigonometry to this triangle.
From the sine theorem, the same value of R will be found from all three sides.
If the other two sides are b and c, the area Δ of the triangle is . Multiplying together these two formulae, .
Replacing a by 2Rsin(A), etc. it follows that
- Δ = 2R2sin(A)sin(B)sin(C).
The circumcentre lies in the interior of a triangle if and only if all the angles are acute. For a right-angled triangle it lies at the centre of the hypotenuse, and if one angle is obtuse it lies outside the triangle. The circumcircle is the smallest circle that can enclose an acute-angled triangle. For an obtuse-angled triangle, the circle with the longest side as a diameter is smaller. (For a right-angled triangle, these two circles are identical.)