Transportation Geography and Network Science/Reliability
The most commonly accepted definition declares reliability to be “the probability that [a] system can perform its desired function to an acceptable level of performance for some given period of time.”[1] This definition is useful but general: any specific measure of reliability will depend on the nature of the desired function and what levels of performance are acceptable. As a result, a wide range of both definitions and measures of reliability have been proposed, each designed for application to a specific type of transportation network or a specific network function.
Introduction
[edit | edit source]Transportation network is a key component to provide a better transport service for both people and goods [2]. Studies have struggled constantly to explore the characteristics of a transport network, including vulnerability, resilience, robustness, and reliability. Understanding these concepts are pivotal for researches and practitioners, since eases addressing the failure of certain nodes, links, or sub-networks which is rooted in car accidents, road maintenance, or serious road congestion. The following sections are trying to introduce the aforesaid concepts in a concise fashion.
Reliability of road network
[edit | edit source]Introduction of reliability of road network
[edit | edit source]The reliability of a transport network is defined as the possibility of moving people or goods from one place to another successfully [3]. Exploring the reliability of a road network has attracted a significant attention since the recent earthquakes, including the Turkey earthquake in 1999 and the Kobe earthquake in 1995 [4]. Such natural disasters not only damage the connections of the roadways, but paralyze the transportation system for a remarkable period of time. For instance, the mobility of the network was completely lost after the Kobe earthquake [5] [6]. Following the development of transportation network in cities, the reliability studies aim to both diminish the natural disasters effects and analyze the unpredictable variations caused by the uncertainties on a road network. Such uncertainties could be resulted from the changes in the supply and demand of transport services [7]. A reliable transport network has the ability to deal with these turbulences to guarantee an acceptable service level [8]. Further, higher reliability for transport networks, the better quality of transportation systems.
Connectivity reliability, travel time reliability, and capacity reliability are three main measures for reliability of a network which are discussed below [9].
The measures of Reliability
[edit | edit source]Connectivity reliability
[edit | edit source]Connectivity is the simplest measurement for reliability, and reflects whether origins and destinations are connected for each OD pairs in a network matrix [10]. Connectivity reliability is defined as the probability of maintaining nodes connected in a transport network [11]. Terminal reliability is a special case in connectivity reliability, which also considers the paths between OD pairs [12]. In other words, terminal reliability reflects the redundancy of a road network in which the alternative routes are used when the connection of certain links is damaged [13].
In a functional expression, for a certain link, its connectivity could be expressed as a binary variable [14],
An example of road network is shown in Figure 1[15], which contains two nodes (A and B) and 5 links connected to these nodes. It is worth to attention that no direction limitation is considered in the network.
Four minimal paths could reach to node B from A, which are [16]
Hence, for such a network, is 1 based on equation (1). If some links are shutdown, the network still has the ability to maintain the connectivity between node A and B. For example, if link 1 does not work, path 2 and path 4 could be used to connect given nodes. If both link 1 and link 2 are disabled, path 2 still could connect node A and B.
However, some cut on the links could make the nodes disconnected. For instance, if both link 1 and link 3 are cut, would be 0, which stands for the disconnection of given nodes.
The reliability of the whole network instead of only two nodes could be expressed as the structure function , in which is a vector of link [17] [18]. For a series network,is the produce of all the , which is . While for a parallel network, the structure function is [19]. The structure function for more complicated network could be derived by the minimal path sets and the minimal cut set. And the value of reliability is the expected value of [20] [21].
Travel time reliability
[edit | edit source]Travel time reliability reflects the uncertainties of travel time. It is defined as “the probability that a trip can reach the destination within a specified time interval” [22] [23]. Travel time reliability reflects the turbulence of daily traffic conditions rather than extreme such as connectivity reliability, natural disasters. And it specified on the turbulence of travel time based on the traffic flow variations. Figure 2 shows average travel time and the daily travel time with turbulence of a segment of Northbound I-5 in 2005 [24].

Travel time reliability shows its importance for the users of all traffic modes in transportation system, such as autos and transit, and for different trip purposes, such as working, traveling, shopping or picking up kids. Hence, the improvement of travel time reliability is necessary to provide a higher quality of transportation system.
In traffic management arena both the average travel time and the travel time reliability are used to optimize the operation of the system. The before and after comparison results show that the travel time reliability is a better measure than the simple average of daily travel time, which is showed in Figure 4 [25].

There are some simple measures, which could evaluate the travel time reliability. The 90th or 95th percentile travel time stands for the longest travel time happened on specific routes, which reflects the worst delay with the heaviest traffic flow. Buffer index is the extra time that needed to arrive the destinations based on the average travel time with 95 percent certainty. While planning time index represents the total travel time to ensure a 95 percent certainty to reach the destinations. The relationship between this three measures is showed in Figure 5 [26].
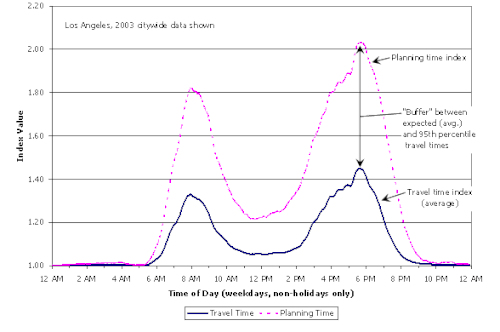
To measure the travel time reliability, the methods are more complicated. Most of the measurements consider the variation of travel time based on normal daily observations of travel time. In this method, the travel time is assumed to follow a normal distribution for each link. The distribution of travel time for an entire path could be computed by combining the distribution of every link of this path. The reliability will be, then, the probability that the travel time plus uncertainty is less than an expected value of travel time [27] [28] [29].
Capacity reliability
[edit | edit source]Capacity reliability is defined as “the probability that the road network can accommodate a certain level of traffic demand based on the reserved capacity of road network" [30]. Hence, capacity reliability could be computed as the probability that the actual travel demand is less than the maximum flow capacity or the highest possible travel demand [31] [32].
The maximum flow capacity is the tricky here, since the many factors could affect the capacity, such as physical design of the roads or the travel behavior on route choice, which should be considered in the estimation process [33]. Network reserve capacity is used to calculate the maximum flow capacity, which could be expressed as the largest multiplier for the OD demand assigned to a transport network without exceeding the limitation of capacity, [34] [35]. The functional expression is showed as below:
Where is the traffic flow of link a on equilibrium with the OD demand of and capacity of .
And the capacity reliability to satisfy the required demand level could be showed as follows,
For calculation the capacity reliability, Chen use the Monte Carlo simulation to estimate the distribution of the [36].
Measures of Reliability in Transportation Networks
[edit | edit source]Terminal Reliability
[edit | edit source]Terminal reliability measures the probability that a transportation network can perform a very basic function: providing a path — any path, regardless of cost — from an origin to a destination. To determine this measure, each link in a network is assigned a functional probability x that represents the likelihood that the link will function at any given time. This will be 1 if the link always functions and 0 if it never functions; intermediate values of x denote links that function x% of the time.[37]
These probabilities can be combined logically. In order for any single path to function, all of the links in that path must function. Since basic probability theory shows that P(A∩B)=P(A)×P(B), the probability that a single path will function is the product of the probabilities of all links in that path. In the case where the origin and destination are connected by more than one path, the network will function as long as any one path functions. Since P(A∪B)=P(A)+P(B)-P(A∩B), the probability that the origin and destination are connected can be calculated after establishing the functional probability of each possible path.[38]
As an example, imagine a national rail network where each link is closed for maintenance two days out of every year. Scheduling of maintenance is handled separately by regional authorities, and a national coordinator wants to evaluate the chance that specific pairs of destinations might become disconnected at some point in a year due to maintenance closures. He assigns each link a functional probability of 363/365 = 99.45%, identifies the possible paths between the points of interest, and applies the logic above to evaluate the reliability of each path and then of the connection.
Travel Time Reliability
[edit | edit source]Travel time reliability refers to the probability that a trip from an origin to a destination can be made in a specific time, or within a given range of times. It is used most often on networks where travel demand fluctuations are to some degree random, such as road networks and other multi-user networks. Travel time reliability should not be confused with delays caused by predictable variations. For example, queues due to bottleneck congestion in the fixed demand case.
Most treatments of travel time reliability establish a baseline travel time through observation and then evaluate how different sources of uncertainty will affect actual travel times. The measured reliability is the probability that the baseline travel time plus uncertainty will be less than a desired value. Uncertainty is generated by two fundamental source: demand variation and capacity variation. Most attempts at describing travel time reliability have been based on the variation of travel time under normal daily (or other cyclical) usage variations. In these studies, each link is generally assumed to offer a normally-distributed range of travel times. These link travel time distributions are combined to compute the probability distribution of travel times for an entire path.[37] [38]
Travel time reliability is analyzed from two approaches: Scheduling Delays with uncertainty, and Mean-Variance. The first assumes travelers have a preferred arrival time, and thus variations around this time time may be classified as schedule early or late delays. The second assumes an average travel time (mean) for the travelers, and variations around this time are classified as variance. Both approaches may be equal under some circumstances [39]
Capacity Reliability
[edit | edit source]Capacity reliability measures the probability that the network can handle a specific amount of demand. It can also be viewed as the probability that a network use will be able to complete a trip without encountering a degraded or over-capacity link. In this sense it is a refinement of terminal reliability, which considers neither link capacity nor user demand and link selection.
Proposed calculations of capacity reliability begin estimating a network’s reserve capacity, which represents the volume of traffic the network can handle above some baseline without reaching its maximum capacity or exceeding some defined service level. Existing studies have modeled reserve capacity as a multiplier applied to the baseline traffic volume. Simulation techniques are then applied to model network users’ responses to degraded links, rerouting network flow as links begin to reach capacity. [37] [38]
References
[edit | edit source]- ↑ Cassir, C., Bell, M., & Iida, Y. (2000). Introduction. In Bell, M. G. H., & Cassir, C. (Eds.), Reliability of transport networks (pp. vii-xi). Philadelphia: Research Studies Press.
- ↑ Rupi, Federico, et al. “The Evaluation of Road Network Vulnerability in Mountainous Areas: A Case Study.” Networks and Spatial Economics (2014): 1-15.
- ↑ Berdica, Katja. “An introduction to road vulnerability: what has been done, is done and should be done.” Transport Policy 9.2 (2002): 117-127.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ Wakabayashi, H., 1996. Reliability Assessment and importance analysis of highway network: a case study of the 1995 Kobe earthquake. In: Proceedings of the First Conference of Hong Kong Society for Transportation Studies, Hong Kong, pp. 155-169.
- ↑ Nicholson, A., et al. “Assessing transport reliability: malevolence and user knowledge.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ Nicholson, A., et al. “Assessing transport reliability: malevolence and user knowledge.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ Lam, W. H. K., and M. L. Tam. “Reliability assessment on searching time for parking in urban areas.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ Lam, W. H. K., and M. L. Tam. “Reliability assessment on searching time for parking in urban areas.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ Chen, Anthony, et al. “Capacity reliability of a road network: an assessment methodology and numerical results.” Transportation Research Part B: Methodological 36.3 (2002): 225-252.
- ↑ WAKABAYASHI, Hiroshi, and Yasunori IIDA. “Upper and lower bounds of terminal reliability of road networks: an efficient method with Boolean algebra.”Journal of Natural Disaster Science 14.1 (1992): 29-44.
- ↑ Berdica, Katja. “An introduction to road vulnerability: what has been done, is done and should be done.” Transport Policy 9.2 (2002): 117-127.
- ↑ Nicholson, A., et al. “Assessing transport reliability: malevolence and user knowledge.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ https://wiki.cecs.pdx.edu/pub/Main/SlidesCE351/16_LOS_in_Highways.pdf
- ↑ http://ops.fhwa.dot.gov/publications/tt_reliability/brochure/ttr_brochure.pdf
- ↑ http://ops.fhwa.dot.gov/publications/tt_reliability/brochure/ttr_brochure.pdf
- ↑ Berdica, Katja. “An introduction to road vulnerability: what has been done, is done and should be done.” Transport Policy 9.2 (2002): 117-127.
- ↑ Nicholson, A., et al. “Assessing transport reliability: malevolence and user knowledge.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ http://en.wikibooks.org/wiki/Transportation_Geography_and_Network_Science/Reliability#cite_note-4
- ↑ Chen, Anthony, et al. “A capacity related reliability for transportation networks.”Journal of advanced transportation 33.2 (1999): 183-200.
- ↑ Chen, Anthony, et al. “A capacity related reliability for transportation networks.”Journal of advanced transportation 33.2 (1999): 183-200.
- ↑ Nicholson, A., et al. “Assessing transport reliability: malevolence and user knowledge.” Network Reliability of Transport. Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). 2003.
- ↑ Chen, Anthony, et al. “A capacity related reliability for transportation networks.”Journal of advanced transportation 33.2 (1999): 183-200.
- ↑ Chen, Anthony, et al. “A capacity related reliability for transportation networks.”Journal of advanced transportation 33.2 (1999): 183-200.
- ↑ Wong, S. C., and Hai Yang. “Reserve capacity of a signal-controlled road network.” Transportation Research Part B: Methodological 31.5 (1997): 397-402.
- ↑ Chen, Anthony, et al. “A capacity related reliability for transportation networks.”Journal of advanced transportation 33.2 (1999): 183-200.
- ↑ a b c Nicholson, A. J., Schmöcker, J-D., Bell, M. G. H., & Iida, Y. (2003). Assessing transport reliability: Malevolence and user knowledge. In Bell, M. G. H., & Iida, Y. (Eds.), The network reliability of transport (pp. 1-22). Oxford: Elsevier Science.
- ↑ a b c Berdica, K. (2002). An introduction to road vulnerability: what has been done, is done and should be done Transport Policy, 9 (2), 117-127 DOI: 10.1016/S0967-070X(02)00011-2
- ↑ Carrion, C. and Levinson, D. (2011), Value of Reliability: A review of current evidence














