Transportation Deployment Casebook/United States Post Office
Introduction[edit | edit source]
The United States Post Office (USPS) services 151 million delivery points in the United States. [1] This network of mailboxes, post offices, sorting facilities, and delivery trucks provides the means for any individual or business to ship goods or information from one destination to another. As electronic means of transmitting information increase in availability and decrease in cost, it is reasonable to expect that this physical postal network will decline in relevance over time. This article examines historical data on the number of post offices in the United States and the volume of mail handled by the post office to identify a birth, growth, maturity, and decline lifecycle for the postal service mode of transport.
Postal Service as a transportation mode[edit | edit source]
Centralized postal service is a coordinated transport system that physically moves goods and information between destinations. It is essentially a freight system that is accessible to any individual or business.
Monopoly and service obligation
Sub-modes: Post offices vs. home delivery[edit | edit source]
The postal service's deployment model originally was a network of post offices and transshipment in between them. Post office customers were responsible for bringing mail to the post office and for picking up their letters and parcels from general delivery to their local post office.
In the 1860's, the postal service started to deploy home/business delivery within urbanized areas. This enabled the closing of post offices, as there was less demand for customer assistance in the post office. Each post office as able to serve a larger area and population base because a network of carriers was deployed to distribute the mail to people's homes and offices.
In the 1890's, the post office began to experiment with rural home delivery to see if it would be feasible. By 1901, rural home delivery was the postal service's official policy. At this point, the number of post offices in the United States began to contract as larger and larger portions of the country were connected to this home delivery network.
This shift from an exclusively post office-oriented network to an expanded point-to-point network connecting all residents is essentially a mode shift within the postal system. It altered the primary role post offices played in the system, shifting their role from a public face and a distribution point to a logistics center coordinating postal carriers, The average number of people to post office continued to increase with population growth and post office consolidation.
Enabling modes[edit | edit source]
Postal service evolved over time to incorporate technological advancements. What started as a horse and carriage operation incorporated river boats, railroads, highways, and eventually air freight.
Competing modes[edit | edit source]
Technological advancements in information technology are supplanting much of the postal service's information-transporting function. The number of pieces of mail handled each year started declining in 2006. When averaged across the population, the number of pieces of mail handled per person has been in decline since 2000.
Data[edit | edit source]
Independent & Control variables[edit | edit source]
Time in years, 1790 to 2010 Population, 1790 to 2010 [2][3][4][5]
Dependent Variables[edit | edit source]
Number of post offices, 1790 to 2010[6]
Number of pieces of mail handled, 1847 to 2010[6]
Constructed Dependent Variables[edit | edit source]
- Number of post offices abandoned
For ,
- Post offices per 10,000 people :
- People per post office :
- Pieces of mail handled per person :
Linear Transformations[edit | edit source]
Dependent variables were transformed to facilitate using a linear regression model.
Methodology[edit | edit source]
Model 1: Dependent variable as a function of time in two phases[edit | edit source]
- Model 1a: Birth, growth, and maturation phase, all years prior to
- Model 1b: Maturation and decline phase, all years following
Dependent variables tested using this model:
- Pieces of mail handled,
- Number of post offices,
- Number of post offices abandoned, , [decline phase only]
- Number of post offices per 10,000 people,
- People per post office,
- Pieces of mail handled per person,
Model 2: Dependent variable as a function of time, controlling for population[edit | edit source]
- Model 2a: Birth, growth, and maturation phase, all years prior to
- Model 2b: Maturation and decline phase, all years following
Dependent variables tested using this model:
- Pieces of mail handled,
- Number of post offices,
- Number of post offices abandoned, , [decline phase only]
Results[edit | edit source]
Descriptive Statistics[edit | edit source]
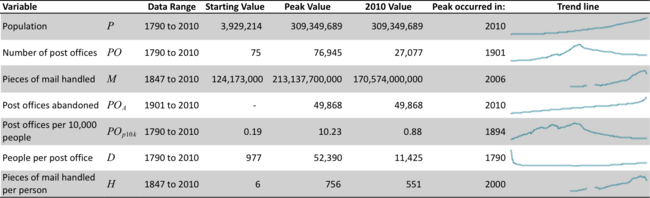
As evident in the Descriptive Statistics table, both the number of post offices and the volume of mail handled have already peaked. Post offices peaked in 1901 when USPS made rural home delivery standard practice. Volume of mail peaked more recently in 2006. Post offices per 10,000 people was highly volatile in the 1800's as USPS rolled out home delivery incrementally.
Notably, both mail handled per person and post offices per 10,000 people peaked before the absolute measures of mail handled and post offices. Even before the rural home delivery policy in 1901 that precipitated the closure of many post offices, fewer post offices were needed to serve the same number of people. This could be explained by urban home delivery, increased efficiency of operations, or better supporting transportation infrastructure. Mail volumes per person peaked in 2000 and has been declining. This can reasonably be explained by shifting information technologies and the rise of electronic transmission supplanting physical print material delivery.
Correlations[edit | edit source]
All of the variables presented in the Dependent Variable Correlations table have a statistically significant correlation with year, population, and transformed population. The direction of these correlations is not unexpected: mail volume has increased dramatically over time and with increasing population, while the number of post offices has declined. The average number of people each post office serves is positively correlated with population both due to the declining number of post offices and the ever-increasing population.
Regression Models[edit | edit source]
Pieces of mail handled over time[edit | edit source]

The mail volumes over time models demonstrate the significance of a growing market in the deployment of this particular transportation "mode". While mail volume has a strong and statistically significant coefficient in Models 1 and 1a, controlling for population in Model 2a eliminates the effect of time. Model 2a fits the growth phase of these data quite well, with an value of 0.977. values for Model 1 and Model 1a are reasonable given the parameters of the data and the qualitative history of USPS and competing modes.
Since the peak volumes of mail handled occurred in 2006, there were not enough data points to conduct a meaningful analysis of the decay phase while controlling for population. Even though Model 1b has t statistic values with a magnitude greater than 2, this model should be considered with caution because it only contains 4 years of data. Conversely, since the decay phase is only evident in the final 4 years of data, the overall models (Model 1 and Model 2) fit the data almost as well as the growth-specific models (Model 1a and Model 2a).
The value for Model 1b reinforces the decay model's weakness: 2010 is the final year of available data, so it is unreasonable to expect with any certainty that 2010 will indeed be the inflection point on the decay curve. The decay model assumes that mail volumes will ultimately drop to zero as other modes replace it quickly, while it is easy to imagine the postal service retaining modest importance as other modes slowly substitute in.
Number of post offices over time[edit | edit source]
Unlike the mail volumes model, post offices peaked in 1901 and the overall models are not a very good fit for the data, with values below 0.355. The coefficients are not consistent with our knowledge of the post office trends: Models 1 and 2 have positive coefficients for time, when it is evident from the graph in the descriptive statistics that the number of post offices has been in decline for over a century.[7]
Both the growth and decay models fit the data much better than the overall models. The coefficients in Models 1a and 1b are consistent with the expected direction of influence and have strong t-statistics. Controlling for population in Models 2a and 2b strengthens the coefficients for time, and they remain statistically significant. Controlling for population also improves the model fit slightly for both the growth and decay phases.
While the decay model failed for mail volumes, the decay model for post offices uses a much longer trajectory of data and is consistent with the slow fizzle of post office coverage over time, rather than the precipitous drop the mail volume model predicted.
The values for Models 1a and 1b are reasonable given the parameters of the data.
Number of post offices abandoned or closed over time[edit | edit source]


These data only required Models 1b and 2b because post office closure did not start until after the number of post offices peaked in 1901.
This model fits the post office data much better than simply the number of post offices from 1901 to 2010. Model 1b has values of 0.941 for the post office closure data and 0.747 for the number of post offices data. Model 2b has values of 0.965 for the post office closure data, again compared to 0.790 for the number of post offices.
As apparent in the Curve Types image to the left, when transformed and adjusted to the same scale, the closed/abandoned curve more closely resembles the S-Curve function we are using to predict the birth, growth, and maturity cycle. The curve representing the actual number of post offices remaining is the inverse of this graph, with steep changes occurring while the closed/abandoned curve is in the more gradual birth and maturity phases. The next image plots these data alongside the projected values using the regression coefficient and calculated from Model 1b.
Ratios of volumes and facilities to population models[edit | edit source]
The final three dependent variables tested are all ratios of mail volumes or post office facilities to total population, so Models 2, 2a, and 2b controlling for population have been eliminated.
Post offices per 10,000 people[edit | edit source]
People per post office[edit | edit source]
Mail volumes per person[edit | edit source]
Discussion[edit | edit source]
These experiments suggest that while the S-Curve model of predicting transportation mode deployment as a function of time fits relatively well, population growth is also a significant driver of deployment. Controlling for population directly through the regression model or indirectly by testing the rate of mail volumes or post office facilities to population facilitated in isolating the effects of population versus time.
The post office facility models best demonstrated the S-curve deployment pattern. The growth models for for number of post offices had high values. Controlling for population increased the strength of the regression coefficient and the value. The decay model for closure/abandonment of post office facilities best modeled the shift to home delivery and then technological mode shift. Controlling for population decreased the regression coefficient but still improved the value.
References[edit | edit source]
- ↑ "Delivery Points, 1905 to 2010, in Millions". Historian, United States Postal Service. 2011. Retrieved 7 October 2011.
{{cite web}}: Unknown parameter|month=ignored (help) - ↑ "US Census History: Fast Facts". Retrieved 7 October 2011.
- ↑ "US Census Historical National Population Estimates, July 1 1900 to July 1 1999". Retrieved 7 October 2011.
- ↑ "US Census National Intercensal Estimates, 2000 to 2010". Retrieved 7 October 2011.
- ↑ Pre-1900 Intercensal population estimates constructed using linear projection:
- ↑ a b "Pieces of Mail Handled, Number of Post Offices, Income, and Expenses, 1789 to 2010". Historian, United States Postal Service. 2011. Retrieved 7 October 2011.
{{cite web}}: Unknown parameter|month=ignored (help) - ↑ J. E. Schoner (2011). "Descriptive Statistics".
{{cite web}}: Unknown parameter|month=ignored (help)