Topology/Simplicial complexes
A simplicial complex is a union of spaces known as simplicies, that are convex hulls of points in general position. In Euclidean space they can be thought of as a generalisation of the triangle. For the first few dimensions they are: the point, the line segment, the triangle and the tetrahedron.
Definition of a simplex
[edit | edit source]Given n+1 points , in a space with dimension of at least n, such that no three points are colinear, the set
is a simplex, and more specifically an n-simplex since it has n+1 verticies.
The standard n-simplex
[edit | edit source]For ease we will sometimes need a standardised co-ordinate system for a simplex. The standard n-simplex, a subset of Euclidean (n+1)-space, , is
Note that the set is expressed in a very similar manner, but the co-ordinates are fixed in .
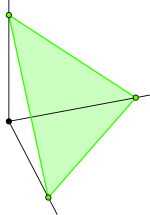
Face of a Simplex
[edit | edit source]A face of an n-simplex is any (n-1)-simplex formed by an n-1 element subset of the verticies of .
Defintion of a simplicial complex
[edit | edit source]A simplicial complex is a union of simplicies such that the intersection of any two simplicies is a simplex. Alternatively if is a simplicial complex then
1. Every face of a simplex in is a simplex in .
2. The intersection of two simplicies is a face of both of A and B.
Example
[edit | edit source]The triangulation of a polygon in the plane is a simplcial complex. In fact it hints at the existence of simplicial complexes existing for all polytopes, e.g. every polyhedron can be expressed as tetrahedrons meeting full face to full face.
Exercises
[edit | edit source](under construction)

![{\displaystyle {\mathcal {S}}=\{t_{0}a_{0}+t_{1}a_{1}+\dots +t_{n}a_{n}:\sum _{i=1}^{n}t_{i}=1{\text{ with }}t_{i}\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78d456e55972b2b33eba3f7d532e17975e49d2fe)




