Before we discuss topological spaces in their full generality, we will first turn our attention to a special type of topological space, a metric space. This abstraction has a huge and useful family of special cases, and it therefore deserves special attention. Also, the abstraction is picturesque and accessible; it will subsequently lead us to the full abstraction of a topological space.
A metric space is a Cartesian pair  where
where  is a non-empty set and
is a non-empty set and  , is a function which is called the metric which satisfies the requirement that for all
, is a function which is called the metric which satisfies the requirement that for all  :
:
 if and only if
if and only if 
 (symmetry)
(symmetry) (triangle inequality)
(triangle inequality)
Note that some authors do not require metric spaces to be non-empty. We annotate  when we talk of a metric space
when we talk of a metric space  with the metric
with the metric  .
.
- An important example is the discrete metric. It may be defined on any non-empty set X as follows

- On the set of real numbers
 , define
, define  (The absolute distance between
(The absolute distance between  and
and  ).
).
To prove that this is indeed a metric space, we must show that  is really a metric. To begin with,
is really a metric. To begin with,  for any real numbers
for any real numbers  and
and  .
.



- On the plane
 as the space, and let
as the space, and let  .
.
- This is the euclidean distance between
 and
and  ).
).
- We can generalize the two preceding examples. Let
 be a normed vector space (over
be a normed vector space (over  or
or  ). We can define the metric to be:
). We can define the metric to be:  . Thus every normed vector space is a metric space.
. Thus every normed vector space is a metric space.
- For the vector space
 we have an interesting norm. Let
we have an interesting norm. Let  and
and  two vectors of
two vectors of  . We define the p-norm:
. We define the p-norm:  . For each
. For each  -norm there is a metric based on it. Interesting cases of
-norm there is a metric based on it. Interesting cases of  are:
are:
- The great-circle distance between two points on a sphere is a metric.
- The Hilbert space is a metric space on the space of infinite sequences
 such that
such that  converges, with a metric
converges, with a metric  .
.
The concept of the Erdős number suggests a metric on the set of all mathematicians. Take  to be two mathematicians, and define
to be two mathematicians, and define  as 0 if
as 0 if  are the same person; 1 if
are the same person; 1 if  have co-authored a paper;
have co-authored a paper;  if the shortest sequence
if the shortest sequence  , where each step pairs two people who have co-authored a paper, is of length
, where each step pairs two people who have co-authored a paper, is of length  ; or
; or  if
if  and no such sequence exists.
and no such sequence exists.
This metric is easily generalized to any reflexive relation (or undirected graph, which is the same thing).
Note that if we instead defined  as the sum of the Erdős numbers of
as the sum of the Erdős numbers of  , then
, then  would not be a metric, as it would not satisfy
would not be a metric, as it would not satisfy  . For example, if
. For example, if  = Stanisław Ulam, then
= Stanisław Ulam, then  .
.
Throughout this chapter we will be referring to metric spaces. Every metric space comes with a metric function. Because of this, the metric function might not be mentioned explicitly. There are several reasons:
- We don't want to make the text too blurry.
- We don't have anything special to say about it.
- The space has a "natural" metric. E.g. the "natural" metric for
 is the euclidean metric
is the euclidean metric  .
.
As this is a wiki, if for some reason you think the metric is worth mentioning, you can alter the text if it seems unclear (if you are sure you know what you are doing) or report it in the talk page.
The open ball is the building block of metric space topology. We shall define intuitive topological definitions through it (that will later be converted to the real topological definition), and convert (again, intuitively) calculus definitions of properties (like convergence and continuity) to their topological definition. We shall try to show how many of the definitions of metric spaces can be written also in the "language of open balls". Then we can instantly transform the definitions to topological definitions.
Given a metric space  an open ball with radius
an open ball with radius  around
around  is defined as the set
is defined as the set

Intuitively it is all the points in the space, that are less than  distance from a certain point
distance from a certain point  .
.
Why is this called a ball? Let's look at the case of  :
:

Therefore  is exactly
is exactly  – The ball with
– The ball with  at center, of radius
at center, of radius  . In
. In  the ball is called open, because it does not contain the sphere (
the ball is called open, because it does not contain the sphere ( ).
).
The Unit ball is a ball of radius 1. Lets view some examples of the  unit ball of
unit ball of  with different
with different  -norm induced metrics. The unit ball of
-norm induced metrics. The unit ball of  with the norm
with the norm  is:
is:
![{\displaystyle B_{1}{\bigl (}(0,0){\bigr )}={\Big \{}(x,y)\in \mathbb {R} ^{2}:d{\bigl (}(x,y),(0,0){\bigr )}<1{\Big \}}={\Big \{}(x,y):{\bigl \|}(x,y)-(0,0){\bigr \|}_{p}<1{\Big \}}={\Big \{}(x,y):\|(x,y)\|_{p}<1{\Big \}}={\Big \{}(x,y):{\sqrt[{p}]{|x|^{p}+|y|^{p}}}<1{\Big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ebf9c0bf5f2d66d2fe08844d3548e60e3a9868)
- The metric induced by
 in that case, the unit ball is:
in that case, the unit ball is: 
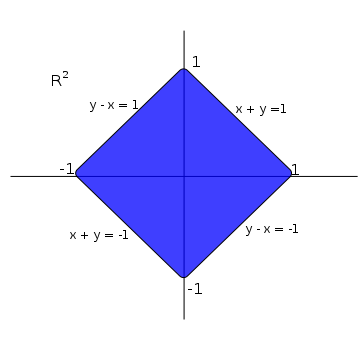
- The metric induced by
 in that case, the unit ball is:
in that case, the unit ball is: 

- The metric induced by
 in that case, the unit ball is:
in that case, the unit ball is: 

As we have just seen, the unit ball does not have to look like a real ball. In fact sometimes the unit ball can be one dot:
- The discrete metric, The unit ball is

Definition: We say that x is an interior point of A iff there is an  such that:
such that:  .
This intuitively means, that x is really 'inside' A - because it is contained in a ball inside A - it is not near the boundary of A.
.
This intuitively means, that x is really 'inside' A - because it is contained in a ball inside A - it is not near the boundary of A.
Illustration:
| Interior Point
|
Not Interior Points
|
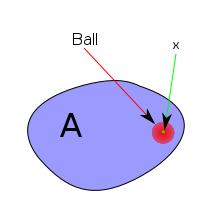
|

|
Definition: The interior of a set A is the set of all the interior points of A. The interior of a set A is marked  .
Useful notations:
.
Useful notations:  and
and  .
.
Some basic properties of int (For any sets A,B):




Proof of the first:
We need to show that:  . But that's easy! by definition, we have that
. But that's easy! by definition, we have that  and therefore
and therefore 
Proof of the second:
In order to show that  , we need to show that
, we need to show that  and
and  .
.
The "  " direction is already proved: if for any set A,
" direction is already proved: if for any set A,  , then by taking
, then by taking  as the set in question, we get
as the set in question, we get  .
.
The "  " direction:
" direction:
let  . We need to show that
. We need to show that  .
.
If  then there is a ball
then there is a ball  . Now, every point y, in the ball
. Now, every point y, in the ball  an internal point to A (inside
an internal point to A (inside  ), because there is a ball around it, inside A:
), because there is a ball around it, inside A:  .
.
We have that  (because every point in it is inside
(because every point in it is inside  ) and by definition
) and by definition  .
.
Hint: To understand better, draw to yourself  .
.
Proof of the rest is left to the reader.
- [a, b] : all the points x, such that

- (a, b) : all the points x, such that

For the metric space  (the line), we have:
(the line), we have:
![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
![{\displaystyle int((a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfed9af226d984832f234c50d6da2f32e3142aed)


Let's prove the first example (![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f) ). Let
). Let  (that is:
(that is:  ) we'll show that
) we'll show that  is an internal point.
is an internal point.
Let  . Note that
. Note that  and
and  . Therefore
. Therefore  .
.
We have shown now that every point x in  is an internal point. Now what about the points
is an internal point. Now what about the points  ? let's show that they are not internal points. If
? let's show that they are not internal points. If  was an internal point of
was an internal point of ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) , there would be a ball
, there would be a ball ![{\displaystyle B_{\epsilon }(a)\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b62496930755059267ae3e9c396cba3aca37dd0) . But that would mean, that the point
. But that would mean, that the point  is inside
is inside ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) . but because
. but because  that is a contradiction. We show similarly that b is not an internal point.
that is a contradiction. We show similarly that b is not an internal point.
To conclude, the set  contains all the internal points of
contains all the internal points of ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) . And we can mark
. And we can mark ![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
A set is said to be open in a metric space if it equals its interior ( ). When we encounter topological spaces, we will generalize this definition of open.
However, this definition of open in metric spaces is the same as that as if we regard our
metric space as a topological space.
). When we encounter topological spaces, we will generalize this definition of open.
However, this definition of open in metric spaces is the same as that as if we regard our
metric space as a topological space.
Properties:
- The empty-set is an open set (by definition:
 ).
).
- An open ball is an open set.
- For any set B, int(B) is an open set. This is easy to see because: int(int(B))=int(B).
- If A,B are open, then
 is open. Hence finite intersections of open sets are open.
is open. Hence finite intersections of open sets are open.
- If
 (for any set if indexes I) are open, then their union
(for any set if indexes I) are open, then their union  is open.
is open.
Proof of 2:
Let  be an open ball. Let
be an open ball. Let  . Then
. Then  .
.
In the following drawing, the green line is  and the brown line is
and the brown line is  . We have found a ball to contain
. We have found a ball to contain  inside
inside  .
.
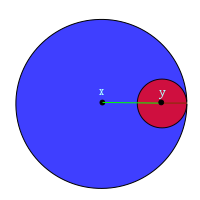
Proof of 4:
A, B are open. we need to prove that  . Because of the first propriety of int, we only need to show that
. Because of the first propriety of int, we only need to show that  , which means
, which means  . Let
. Let  . We know also, that
. We know also, that  from the premises A, B are open and
from the premises A, B are open and  . That means that there
are balls:
. That means that there
are balls:  . Let
. Let  , we have that
, we have that  .
By the definition of an internal point we have that
.
By the definition of an internal point we have that  (
( is the required ball).
is the required ball).
Interestingly, this property does not hold necessarily for an infinite intersection of open sets. To see an example on the real line, let  . We then see that
. We then see that  which is closed.
which is closed.
Proof of 5:
Proving that the union of open sets is open, is rather trivial: let  (for any set if indexes I) be a set of open sets.
we need to prove that
(for any set if indexes I) be a set of open sets.
we need to prove that  : If
: If  then it has a ball
then it has a ball  . The same ball that made a point an internal point in
. The same ball that made a point an internal point in  will make it internal in
will make it internal in
 .
.
Proposition: A set is open, if and only if it is a union of open-balls.
Proof: Let A be an open set. by definition, if  there there a ball
there there a ball  . We can then compose A:
. We can then compose A:  . The equality is true because:
. The equality is true because:  because
because  .
.  in each ball we have the element
in each ball we have the element  and we unite balls of all the elements of
and we unite balls of all the elements of  .
.
On the other hand, a union of open balls is an open set, because every union of open sets is open.
- As we have seen, every open ball is an open set.
- For every space
 with the discrete metric, every set is open.
with the discrete metric, every set is open.
Proof: Let  be a set. we need to show, that if
be a set. we need to show, that if  then
then  is an internal point. Lets use the ball around
is an internal point. Lets use the ball around  with radius
with radius  . We have
. We have  . Therefore
. Therefore  is an internal point.
is an internal point.
- The space
 with the regular metric. Every open segment
with the regular metric. Every open segment  is an open set. The proof of that is similar to the proof that
is an open set. The proof of that is similar to the proof that ![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f) , that we have already seen.
, that we have already seen.
In any metric space X, the following three statements hold:
- 1) The union of any number of open sets is open.
- Proof: Let
 be a collection of open sets, and let
be a collection of open sets, and let
 . Then there exists a
. Then there exists a  such that
such that  .
.- So there exists an
 such that
such that  . Therefore
. Therefore
 .
.
- 2) The intersection of a finite number of open sets is open.
- Proof: Let
 , where
, where  is a finite collection of open sets.
is a finite collection of open sets.
- So
 for each
for each  . Let
. Let  . For each
. For each  , there exists an
, there exists an  such that
such that  . Let
. Let  {
{ }. Therefore
}. Therefore  and
and  .
.
- 3) The empty set and X are both open.
In any metric space X, the following statements hold:
- 1) The intersection of any number of closed sets is closed.
- 2) The union of a finite number of closed sets is closed.
First, Lets translate the calculus definition of convergence, to the "language" of metric spaces:
We say that a sequence  converges to
converges to  if for every
if for every  exists
exists  that for each
that for each  the following holds:
the following holds:  .
.
Equivalently, we can define converges using Open-balls: A sequence  converges to
converges to  If for every
If for every  exists
exists  that for each
that for each  the following holds:
the following holds:  .
.
The latter definition uses the "language" of open-balls, But we can do better - We can remove the  from the definition of convergence, thus making the definition more topological. Let's define that
from the definition of convergence, thus making the definition more topological. Let's define that  converges to
converges to  (and mark
(and mark  ) , if for every ball
) , if for every ball  around
around  , exists
, exists  that for each
that for each  the following holds:
the following holds:  .
.  is called the limit of the sequence.
is called the limit of the sequence.
The definitions are all the same, but the latter uses topological terms, and can be easily converted to a topological definition later.
- If a sequence has a limit, it has only one limit.
Proof Let a sequence  have two limits,
have two limits,  and
and  . If they are not the same, we must have
. If they are not the same, we must have  . Let
. Let  be smaller than this distance. Now for some
be smaller than this distance. Now for some  , for all
, for all  , it must be the case that both
, it must be the case that both  and
and  by virtue of the fact
by virtue of the fact  and
and  are limits. But this is impossible; the two balls are separate. Therefore the limits are coincident, that is, the sequence has only one limit.
are limits. But this is impossible; the two balls are separate. Therefore the limits are coincident, that is, the sequence has only one limit.
- If
 , then almost by definition we get that
, then almost by definition we get that  . (
. ( Is the sequence of distances).
Is the sequence of distances).
- In
 with the natural metric, The series
with the natural metric, The series  converges to
converges to  . And we note it as follows:
. And we note it as follows: 
- Any space, with the discrete metric. A series
 converges, only if it is eventually constant. In other words:
converges, only if it is eventually constant. In other words:  If and only if, We can find
If and only if, We can find  that for each
that for each  ,
, 
- An example you might already know:
The space  For any p-norm induced metric, when
For any p-norm induced metric, when  . Let
. Let  . and let
. and let  .
.
Then,  If and only if
If and only if  .
.
A sequence of functions  is said to be uniformly convergent on a set
is said to be uniformly convergent on a set  if for any
if for any  , there exists an
, there exists an  such that when
such that when  and
and  are both greater than
are both greater than  , then
, then  for any
for any  .
.
Definition: The point  is called a point of closure of a set
is called a point of closure of a set  if there exists a sequence
if there exists a sequence  , such that
, such that  .
.
In other words, the point  is a point of closure of a set
is a point of closure of a set  if there exists a sequence in
if there exists a sequence in  that converges on
that converges on  . Note that
. Note that  is not necessarily an element of the set
is not necessarily an element of the set  .
.
An equivalent definition using balls: The point  is called a point of closure of a set
is called a point of closure of a set  if for every open ball
if for every open ball  containing
containing  , we have
, we have  . In other words, every open ball containing
. In other words, every open ball containing  contains at least one point in
contains at least one point in  that is distinct from
that is distinct from  .
.
The proof is left as an exercise.
Intuitively, a point of closure is arbitrarily "close" to the set  . It is so close, that we can find a sequence in the set that converges to any point of closure of the set.
. It is so close, that we can find a sequence in the set that converges to any point of closure of the set.
Example: Let A be the segment  , The point
, The point  is not in
is not in  , but it is a point of closure: Let
, but it is a point of closure: Let  .
.  (
( , and therefore
, and therefore  ) and
) and  (that's because
(that's because  ).
).
Definition: The closure of a set 
 , is the set of all points of closure. The closure of a set A is marked
, is the set of all points of closure. The closure of a set A is marked  or
or  .
.
Note that  . a quick proof: For every
. a quick proof: For every  , Let
, Let  .
.
For the metric space  (the line), and let
(the line), and let  we have:
we have:
![{\displaystyle Cl([a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eddea72fcc1b24b538915dc798b35c9bf0f3fb)
![{\displaystyle Cl((a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3263fd4ba19f933af00b15ad9b530b4455eef1)
![{\displaystyle Cl([a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40b72d26c5687837bdeeb35c34f4d57fead95a1)
![{\displaystyle Cl((a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b4a77748d74b5fd1519d82516bb94536a551e4c)
Definition: A set  is closed in
is closed in  if
if  .
.
Meaning: A set is closed, if it contains all its point of closure.
An equivalent definition is: A set  is closed in
is closed in  If for every point
If for every point  , and for every Ball
, and for every Ball  , then
, then  .
.
The proof of this definition comes directly from the former definition and the definition of convergence.
Some basic properties of Cl (For any sets  ):
):



 is closed iff
is closed iff 
- While the above implies that the union of finitely many closed sets is also a closed set, the same does not necessarily hold true for the union of infinitely many closed sets. To see an example on the real line, let
![{\displaystyle A_{n}=\{[-1+{\frac {1}{n}},1-{\frac {1}{n}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf2e9facb6e8ad24c28f16409da14b5b4bbede9) . We see that
. We see that  fails to contain its points of closure,
fails to contain its points of closure, 
This union can therefore not be a closed subset of the real numbers.
The proofs are left to the reader as exercises. Hint for number 5: recall that
 .
.
That is, an open set approaches its boundary but does not include it; whereas a closed set includes every point it approaches. These two properties may seem mutually exclusive, but they are not:
- In any metric space
 , the set
, the set  is both open and closed.
is both open and closed.
- In any space with a discrete metric, every set is both open and closed.
- In
 , under the regular metric, the only sets that are both open and closed are
, under the regular metric, the only sets that are both open and closed are  and
and  . However, some sets are neither open nor closed. For example, a half-open range like
. However, some sets are neither open nor closed. For example, a half-open range like  is neither open nor closed. As another example, the set of rationals is not open because an open ball around a rational number contains irrationals; and it is not closed because there are sequences of rational numbers that converge to irrational numbers (such as the various infinite series that converge to
is neither open nor closed. As another example, the set of rationals is not open because an open ball around a rational number contains irrationals; and it is not closed because there are sequences of rational numbers that converge to irrational numbers (such as the various infinite series that converge to  ).
).
A Reminder/Definition: Let  be a set in the space
be a set in the space  . We define the complement of
. We define the complement of  ,
,  to be
to be  .
.
A Quick example: let ![{\displaystyle X=[0,1];A=[0,{\frac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75af4dbbe6e599bdd809a5d967e32f3ddafa812b) . Then
. Then ![{\displaystyle A^{c}=({\frac {1}{2}},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f47e141c6a629e6f8a87585a26f934671bbf47a) .
.
A very important Proposition: Let  be a set in the space
be a set in the space  . Then, A is open iff
. Then, A is open iff  is closed.
is closed.
Proof: ( ) For the first part, we assume that A is an open set. We shall show that
) For the first part, we assume that A is an open set. We shall show that  . It is enough to show that
. It is enough to show that  because of the properties of closure. Let
because of the properties of closure. Let  (we will show that
(we will show that  ).
).
for every ball  we have, by definition that (*)
we have, by definition that (*) . If the point is not in
. If the point is not in  then
then  .
.  is open and therefore, there is a ball
is open and therefore, there is a ball  , such that:
, such that:  , that means that
, that means that  , contradicting (*).
, contradicting (*).
( ) On the other hand, Lets a assume that
) On the other hand, Lets a assume that  is closed, and show that
is closed, and show that  is open. Let
is open. Let  be a point in
be a point in  (we will show that
(we will show that  ). If
). If  is not in
is not in  then for every ball
then for every ball  we have that
we have that  . That means that
. That means that  . And by definition of closure point
. And by definition of closure point  is a closure point of
is a closure point of  so we can say that
so we can say that  .
.  is closed, and therefore
is closed, and therefore  That contradicts the assumption that
That contradicts the assumption that 
Note that, as mentioned earlier, a set can still be both open and closed!
The following is an important theorem characterizing open and closed sets on  .
.
Theorem: An open set  in
in  is the union of countably many disjoint open intervals.
is the union of countably many disjoint open intervals.
Proof: Let  . Let
. Let  and let
and let  . There exists an open ball
. There exists an open ball  such that
such that  because
because  is open. Thus, a≤x-ε and b≥x+ε. Thus, x ∈(a,b). The set O contains all elements of (a,b) since if a number is greater than a, and less than x but is not within O, then a would not be the supremum of {t|t∉O, t<x}. Similarly, if there is a number is less than b and greater than x, but is not within O, then b would not be the infimum of {t|t∉O, t>x}. Thus, O also contains (a,x) and (x,b) and so O contains (a,b). If y≠x and y∈(a,b), then the interval constructed from this element as above would be the same. If y<a, then inf{t|t∉O, t>y} would also be less than a because there is a number between y and a which is not within O. Similarly if y>b, then sup{t|t∉O, t<y} would also be greater than b because there is a number between y and b which is not within O. Thus, all possible open intervals constructed from the above process are disjoint. The union of all such open intervals constructed from an element x is thus O, and so O is a union of disjoint open intervals. Because the rational numbers is dense in R, there is a rational number within each open interval, and since the rational numbers is countable, the open intervals themselves are also countable.
is open. Thus, a≤x-ε and b≥x+ε. Thus, x ∈(a,b). The set O contains all elements of (a,b) since if a number is greater than a, and less than x but is not within O, then a would not be the supremum of {t|t∉O, t<x}. Similarly, if there is a number is less than b and greater than x, but is not within O, then b would not be the infimum of {t|t∉O, t>x}. Thus, O also contains (a,x) and (x,b) and so O contains (a,b). If y≠x and y∈(a,b), then the interval constructed from this element as above would be the same. If y<a, then inf{t|t∉O, t>y} would also be less than a because there is a number between y and a which is not within O. Similarly if y>b, then sup{t|t∉O, t<y} would also be greater than b because there is a number between y and b which is not within O. Thus, all possible open intervals constructed from the above process are disjoint. The union of all such open intervals constructed from an element x is thus O, and so O is a union of disjoint open intervals. Because the rational numbers is dense in R, there is a rational number within each open interval, and since the rational numbers is countable, the open intervals themselves are also countable.
- In any metric space, a singleton
 is closed. To see why, consider the open set,
is closed. To see why, consider the open set,  . Let
. Let  . Then
. Then  , so
, so  . Let
. Let  . Then
. Then  . So
. So  is open, and hence
is open, and hence  is closed.
is closed.
- In any metric space, every finite set
 is closed. To see why, observe that
is closed. To see why, observe that ![{\displaystyle T^{c}={\Big [}\bigcup \{x_{i}\}{\Big ]}^{c}=\bigcap \{x_{i}\}^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f52781672e933ec9a82a7eade5bb4f87a5175d2) is open, so
is open, so  is closed.
is closed.
- Closed intervals [a,b] are closed.
- Cantor Set Consider the interval [0,1] and call it C0. Let A1 be equal {0,
 } and let dn =
} and let dn =  . Let An+1 be equal to the set An∪{x|x=a+2dn, a∈An}. Let Cn be
. Let An+1 be equal to the set An∪{x|x=a+2dn, a∈An}. Let Cn be  {[a,a+dn]}, which is the finite union of closed sets, and is thus closed. Then the intersection
{[a,a+dn]}, which is the finite union of closed sets, and is thus closed. Then the intersection  is called the Cantor set and is closed.
is called the Cantor set and is closed.
- Prove that a point x has a sequence of points within X converging to x if and only if all balls containing x contain at least one element within X.
- In
 the only sets that are both open and closed are the empty set, and the entire set. This is not the case when you look at
the only sets that are both open and closed are the empty set, and the entire set. This is not the case when you look at  . Give an example of a set which is both open and closed in
. Give an example of a set which is both open and closed in  .
.
- Let
 be a set in the space
be a set in the space  . Prove the following:
. Prove the following:


Let's recall the idea of continuity of functions. Continuity means, intuitively, that you can draw a function on a paper, without lifting your pen from it. Continuity is important in topology. But let's start in the beginning:
The classic delta-epsilon definition: Let  be spaces. A function
be spaces. A function  is continuous at a point
is continuous at a point  if for all
if for all  there exists a
there exists a  such that:
for all
such that:
for all  such that
such that  , we have that
, we have that  .
.
Let's rephrase the definition to use balls: A function  is continuous at a point
is continuous at a point  if for all
if for all  there exists
there exists  such that the following holds:
for every
such that the following holds:
for every  such that
such that  we have that
we have that  . Or more simply:
. Or more simply:

Looks better already! But we can do more.
Definitions:
- A function is continuous in a set S if it is continuous at every point in S.
- A function is continuous if it is continuous in its entire domain.
Proposition:
A function  is continuous, by the definition above
is continuous, by the definition above  for every open set
for every open set  in
in  , The inverse image of
, The inverse image of  ,
,  , is open in
, is open in  . That is, the inverse image of every open set in
. That is, the inverse image of every open set in  is open in
is open in  .
.
Note that  does not have to be surjective or bijective for
does not have to be surjective or bijective for  to be well defined. The notation
to be well defined. The notation  simply means
simply means  .
.
Proof:
First, let's assume that a function  is continuous by definition (The
is continuous by definition (The  direction). We need to show that for every open set
direction). We need to show that for every open set  ,
,  is open.
is open.
Let  be an open set. Let
be an open set. Let  .
.
 is in
is in  and because
and because  is open, we can find and
is open, we can find and  , such that
, such that  . Because f is continuous, for that
. Because f is continuous, for that  , we can find a
, we can find a  such that
such that  . that means that
. that means that  , and therefore,
, and therefore,  is an internal point. This is true for every
is an internal point. This is true for every  - meaning that all the points in
- meaning that all the points in  are internal points, and by definition,
are internal points, and by definition,  is open.
is open.
( )On the other hand, let's assume that for a function
)On the other hand, let's assume that for a function  for every open set
for every open set  ,
,  is open in
is open in  . We need to show that
. We need to show that  is continuous.
is continuous.
For every  and for every
and for every  , The set
, The set  is open in
is open in  . Therefore the set
. Therefore the set  is open in
is open in  . Note that
. Note that  . Because
. Because  is open, that means that we can find a
is open, that means that we can find a  such that
such that  , and we have that
, and we have that  .
.
The last proof gave us an additional definition we will use for continuity for the rest of this book. The beauty of this new definition is that it only uses open-sets, and there for can be applied to spaces without a metric, so we now have two equivalent definitions which we can use for continuity.
- Let
 be any function from any space
be any function from any space  , to any space
, to any space  , were
, were  is the discrete metric. Then
is the discrete metric. Then  is continuous. Why? For every open set
is continuous. Why? For every open set  , the set
, the set  is open, because every set is open in a space with the discrete metric.
is open, because every set is open in a space with the discrete metric.
- Let
 The identity function.
The identity function.  is continuous: The source of every open set is itself, and therefore open.
is continuous: The source of every open set is itself, and therefore open.
- Prove that a function
 is continuous
is continuous  for every closed set
for every closed set  in
in  , The inverse image of
, The inverse image of  ,
,  , is closed in
, is closed in  .
.
In a metric space X, function from X to a metric space Y is uniformly continuous if for all  , there exists a
, there exists a  such that for all
such that for all  ,
,  implies that
implies that  .
.
An isometry is a surjective mapping  , where
, where  and
and  are metric spaces and for all
are metric spaces and for all  ,
,  .
.
In this case,  and
and  are said to be isometric.
are said to be isometric.
Note that the injectivity of  follows from the property of preserving distance:
follows from the property of preserving distance:




So an isometry is necessarily bijective.
- Show that a set is a metric open set iff it is a (possibly infinite) union of open balls.
- Show that the discrete metric is in fact a metric.

































































![{\displaystyle B_{1}{\bigl (}(0,0){\bigr )}={\Big \{}(x,y)\in \mathbb {R} ^{2}:d{\bigl (}(x,y),(0,0){\bigr )}<1{\Big \}}={\Big \{}(x,y):{\bigl \|}(x,y)-(0,0){\bigr \|}_{p}<1{\Big \}}={\Big \{}(x,y):\|(x,y)\|_{p}<1{\Big \}}={\Big \{}(x,y):{\sqrt[{p}]{|x|^{p}+|y|^{p}}}<1{\Big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ebf9c0bf5f2d66d2fe08844d3548e60e3a9868)

































![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
![{\displaystyle int((a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfed9af226d984832f234c50d6da2f32e3142aed)










![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle B_{\epsilon }(a)\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b62496930755059267ae3e9c396cba3aca37dd0)





































































































![{\displaystyle Cl([a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eddea72fcc1b24b538915dc798b35c9bf0f3fb)
![{\displaystyle Cl((a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3263fd4ba19f933af00b15ad9b530b4455eef1)
![{\displaystyle Cl([a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40b72d26c5687837bdeeb35c34f4d57fead95a1)
![{\displaystyle Cl((a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b4a77748d74b5fd1519d82516bb94536a551e4c)








![{\displaystyle A_{n}=\{[-1+{\frac {1}{n}},1-{\frac {1}{n}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf2e9facb6e8ad24c28f16409da14b5b4bbede9)








![{\displaystyle X=[0,1];A=[0,{\frac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75af4dbbe6e599bdd809a5d967e32f3ddafa812b)
![{\displaystyle A^{c}=({\frac {1}{2}},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f47e141c6a629e6f8a87585a26f934671bbf47a)



























![{\displaystyle T^{c}={\Big [}\bigcup \{x_{i}\}{\Big ]}^{c}=\bigcap \{x_{i}\}^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f52781672e933ec9a82a7eade5bb4f87a5175d2)




















































