Topological String Theory Methods of Computer-aided Drug Design/Knots, HOMFLY-PT Polynomial, Chern-Simons Theory and Surgery/Knot theory

In this section we are going to review the basics of knot theory. The history of knot theory dates back to ancient times, but the modern mathematical take on the theory started during the early 20^th century.

The following video offers a good introduction to knot theory:

Knots

In mathematics a knot $K:S^{1}\hookrightarrow S^{3}$ is a continuous homeomorphism of a circle ($S^{1}$) to the $3$-sphere ($S^{3}=\{(x,y,z,t)\in \mathbb {R} ^{4}|x^{2}+y^{2}+z^{2}+t^{2}=1\}$)

$S^{3}$ is also called the one-point compactification of the Euclidean $3$-dimensional space ($\mathbb {R} ^{3}=\{(x,y,z)|x,y,z\in \mathbb {R} \}$), which one can view as the usual Euclidean $3$-dimensional space, but with the points at infinity identified as one, i.e. assuming there are no other barriers, a person inside the manifold can see his back, because the light rays that come from his back goes through the point at infinity and comes back in the opposite direction and reaches his eyes.

Some examples of knots are given below.

Table of knots up to $7$ crossings

• 
  Unknot ($0_{1}$)
• 
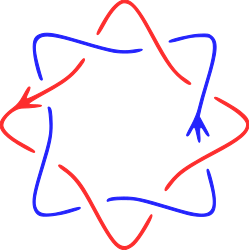
  Trefoil knot ($3_{1}$, also called the $(2,3)$-torus knot or $(3,2)$-torus knot)

Two knots $K_{1}$ and $K_{2}$ are called the same, denoted $K_{1}=K_{2}$, if there is an ambient isotopy, i.e. a continuous mapping $H:S^{3}\times [0,1]\rightarrow S^{3}$ such that

• For each $t\in [0,1]$, the mapping $H(-,t):x\in S^{3}\mapsto H(x,t)\in S^{3}$ is an orientation-preserving homeomorphism.
• $H(x,0)=x$ for all $x\in S^{3}$
• $H(K_{1},1)=K_{2}$

In other words, two knots are the same if one can be continuously deformed into the other without crossing each other.

Links

In knot theory, it is natural to generalize the concept of knots to links, where, instead of $1$ circle, we consider $\mu$ copies of the circle in $S^{3}$, where $\mu =0,1,2,...\in \mathbb {Z} _{\geq 0}$, with no self-intersections in $S^{3}$. Each circle in the link $L$ is called a component, and the number of components is usually denoted by $\mu (L)$.

Examples of links are given below:

• 
  Hopf link
• 
  Borromean rings
• 
  $(2,4)$-torus link

The equivalence of links is similar to that for knots, i.e. by the existence of an ambient isotopy.

Regular diagrams and Reidemeister moves

Links are usually visualized using projections onto a plane that have intersection points between only two portions of the curves. The portion at a higher altitude is drawn continuously, and that at a lower altitude is drawn broken by convention. Diagrams obtained this way are called regular diagrams $D(L)$ of a link $L$.

An important question in knot theory is the so-called recognition problem: given two links $L_{1}$ and $L_{2}$, prove or disprove that $L_{1}=L_{2}$.

It is therefore natural to ask if one can reduce the problem of showing $L_{1}=L_{2}$ into that of showing $D(L_{1})\sim D(L_{2})$ for some equivalence relation $\sim$. The answer is yes: we denote $D(L_{1})\sim D(L_{2})$ if $D(L_{1})$ can be converted to $D(L_{2})$ by a finite sequence of Reidemeister moves, their inverses and planar isotopy.

The Reidemeister moves are given by:

• 
  Reidemeister move 1 ($\Omega _{1}$)
• 
  Reidemeister move 2 ($\Omega _{2}$)
• 
  Reidemeister move 3 ($\Omega _{3}$)

For example, the following shows how to convert a regular diagram into an unknot:

Unknotting a complicated regular diagram

It is Reidemeister's theorem that $L_{1}=L_{2}\iff D(L_{1})\sim D(L_{2})$.

Disproving that two links $L_{1},L_{2}$ are not the same, i.e. proving $L_{1}\neq L_{2}$, is much more difficult, and will be discussed in the next section.