Three Dimensional Electron Microscopy/3D Reconstruction
3D Reconstruction
[edit | edit source]
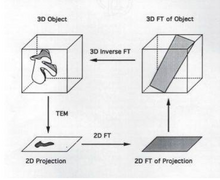



The goal of 3D reconstruction in transmission electron microscopy is to take a 2D projection and turn it into its 3D volume. This allows for the visualization of small structures within the sample. It is essential to reconstruct the 2D projection because the information gained from the projection itself is limited.
Projection
[edit | edit source]A projection occurs when a 3D image is taken and those points are then put onto a 2D plane. Each point in the 2D plane corresponds to a slice in the 3D volume and is based on Radon's theorem. It is possible to obtain a 3D volume, get the 2D projection, subsequently take the Fourier transform of the projection and use the Fourier transform of the projection to obtain a "slice" of the 3D volume. Thereafter, it is possible to take the inverse Fourier transform of the "slice" yielding a 3D volume.
Orientation of the Object
[edit | edit source]Before proceeding to reconstruction, it is necessary to know in which direction the particles are facing. The orientation of the particles can be determined by using their Euler Angles. Euler angles can be defined in two ways. According to the first definition, the orientation can be determined by using the latitude, longitude and rotation in place of the particle. The second definition takes into account the z and x axis. The initial position is determined using the Z axis. Next, the particle is rotated and the orientation is derived from the new X axis. The third and final calculation is based on the location of the new Z axis, after it has been rotated around its x axis.
What is a Backprojection?
[edit | edit source]A backprojection is basically the inverse of a Radon transform. It is the process where a 2D projection goes into a 3D model. It is the only method that can be used for this purpose. A backprojection reconstructs an image by taking each view and smearing it along the same path it was acquired (Fig. 1). The result from this is a blurry version of the correct image (Voss 2013)[1].
Resolution
[edit | edit source]Once a 3D reconstruction is obtained it is important to determine how good the reconstruction is. This is done by using the Fourier Shell Correlation. Essentially the primary set of particles is divided into an even subset and an odd subset in which a structure is calculated for each subset. Each set is then backprojected to obtain a volume for each subset. Since the goal is to determine the quality of the reconstruction the data is divided into rings within Fourier space with each ring representing different resolutions. The Correlation coefficient is then calculated between the structure for the even subset and the odd subset based on their frequency.

Footnotes
[edit | edit source]- ↑ Voss, Neil. 3D Reconstruction. Protein Structure 464. Roosevelt University, Schaumburg, IL. 25 Oct. 2013. Lecture.