Three Dimensional Electron Microscopy/2D particle alignment
What is Alignment?
[edit | edit source]
Alignment is the process of rotating and shifting particles in order to position them in a similar direction. In order to obtain a proper averaged 2D image of the particle, the aligning process is used [1]. Most alignment methods require the particles to be centered. There are multiple approaches when it comes to 2D particle alignment. The main type of classification involves the accessibility to a reference image, dividing methodology into Reference-based alignment and Reference-free alignment
Reference Based Alignment
[edit | edit source]Reference Based Alignment involves a process of aligning every particle in its position and orientation with the reference image. In this approach the particles might be turned over and a mirror orientation needs to be applied. This is followed by an assessment of cross-correlation coefficient in order to establish the resemblance between a particle and a reference. There are many advantages to reference-based alignment. For instance, the technique is fast, effortless to perform, and since the reference is known it allows a visual verification of accurate orientation of the particle in interest. On the other hand, Reference Based Alignment also has drawbacks. The particle alignment can be biased. This is because of the assumption that the particle needs to look like the available reference image. Aligning the particle to faulty reference will result in a noisy data, which will look like the reference. This makes it difficult when evaluating for similarity. It is necessary to decipher if the resemblance is actual or if it is a product of the noise.
Reference-free Alignment
[edit | edit source]Reference-free Alignment is commonly used when there is no apparent assemblage in a data set and the reference images are not available. This particular technique looks for all the possible pairs in an entire data set that have the best comparative orientation. It is computed by applying the cross-correlation function. This method makes use of the random approximation algorithm of overall averages and iterations until convergence is reached. Reference-free alignment has certain advantages. The algorithm used in this method allows shift and rotational alignment of a series of images. It is also fast and requires only the radius of the particle. One of the main disadvantages of this method is the difficulty in aligning the particles that have multiple shapes, low signal to noise ratio or very small data sets. Technically, all reference free methods create a reference for processing data set.
Methods of Alignment
[edit | edit source]Classic Method of 2D Alignment
[edit | edit source]Classic Method of 2D Alignment is a reference based technique. It involves a shift in x and y coordinates, followed by an image rotation in plane, while making a comparison to the reference. Every rotation is tagged along by computation of cross-correlation between image and a reference. The highest cross-correlation value coincides with the best alignment.
Spider Method
[edit | edit source]Spider Method, also known as ring-based correlation, makes use of the rings. It takes different rings of pixels and cuts them up into little circles, lays them flat and stacks the rings in order to cross-correlate them. Instead of doing the x, y shift, the best correlation value is represented by the angle. This method is characterized by a lot of noise resulting in false positive.
Radon Transform
[edit | edit source]
Radon Transform is a useful in techniques like pattern recognition and image processing. It involves the cross sectional scans of the images. It takes the average to make a slice of the image after every rotation around its center. The stack of slices is the final radon transformation of the image. The next step in the process involves the angle approximation that can be calculated by the y shift of the radon transform, which corresponds to the angle of the reference image. This can also be done by using cross correlation in which the highest peak will give the best angle. The final step engages the rotation of the image to its reference. In addition to the averaging process, this method also calculates the error measures and resolution used in 2D alignment technique. Radon transform follows the 3D reconstruction process where translational and rotational alignments can be done in 2D and 3D [2].
Maximum Likelihood (ML)
[edit | edit source]Maximum Likelihood or ML is a reference free method, which involves finding the most probable model to fit in the obtained data. In this approach the probability of observations are measured. These are based on the original model and it is an alternative method to cross correlation technique that makes choice based on differences throughout the data set. ML method assesses the relative orientations of the particles, which are processed as concealed variables that are incorporated in likelihood computation. This ML refinement approach also considers the error model which in turn reduces the biased in the large data sets [3]. It is one of the slowest methods since it involves large data sets.
Classification
[edit | edit source]
Classification is an important step prior to the 3D reconstruction step. There is a strict requirement that individual images used for reconstruction should have. These are different views of the same biological specimen under study. It allows separating the different views of particles from a homogenous set of population. As in the case of a Gro-El molecule, classification applies as separating the top view and side view (Pascual-Montano 233-245).
Principal Component Analysis
[edit | edit source]Principal Component Analysis is used in image recognition and compression techniques. It is known as a mathematical method of grouping things together, followed by reducing their dimensionality, while preserving data that is closest to the original set. This attribute works well when there is a strong correlation between the recorded variable where it projects data along eigenvector. First it converts images into large matrix data. Next it analyzes the key features of different views and creates Eigen-images that have assigned Eigen values. The main functions of this method are to reduce redundancy, extract the general features, and make predictions of the images and data compression. This method is commonly used in the process of face recognition, where it finds the key features that separate the classes of images [4].
Self-Organizing Maps
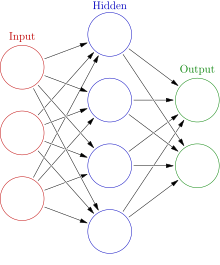
[edit | edit source]Self-Organizing Maps are an excellent method of Data Mapping and Classifying when there is a large number of dataset and classes. This is useful, particularly if the boundaries between the classes are not clear. SOM is also called Kohonen Self Organizing Maps, because these were first discovered by Kohenen in 1997 [5]. SOM is a non-linear projection of high dimensional data in a low dimensional space. The structure of a neural network consists of 3 layers. These are the input layer, middle- hidden layer and the output layer. The SOM simulates the self-organizing process conducted by the human brain when input data is presented to it.
References
[edit | edit source]- ↑ "Methodology of 2D Particle Alignment." Wadsworth Center, [Online]. Accessed 16 Nov. 2013. Available from: http://spider.wadsworth.org/spider_doc/spider/docs/align.html
- ↑ Radermacher. M., (1997) Radon Transform techniques for Alignment and Three Dimensional Reconstruction from Random Projections. Scanning Microscopy Vol. 11, (171-177)
- ↑ Scheres.S.H.W., Valle.M., Nunez.R., Sorzano.C.O.S., Marabini.R., Herman.G.T., Carazao.J.M., (2005) Maximum-Likelihood Multi reference Refinement for Electron Microscopy Images. J. Mol. Biol. 348, (139–149)
- ↑ Kyungnam.K., “Face Recognition using Principal Component Analysis” University of Maryland, [Online]. Accessed 16 Nov. 2013. Available from: http://www.umiacs.umd.edu/~knkim/KG_VISA/PCA/FaceRecog_PCA_Kim.pdf
- ↑ Pascual-Montano A., Donate L.E., Valle M., Barcena M., Pascual-Marqui R.D., Carazo J.M., (2001) A Novel Neural Network Technique for Analysis and Classification of EM Single-Particle Images. Journal of Structural Biology 133,233-245