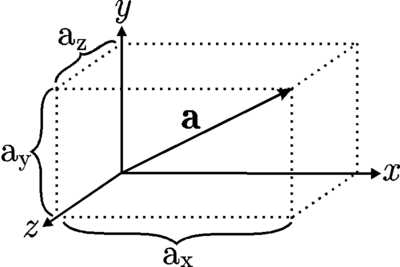
A vector is a quantity that has both a magnitude and a direction. Vectors can be visualized as arrows. The following figure shows what we mean by the components  of a vector
of a vector 
The sum  of two vectors has the components
of two vectors has the components 
- Explain the addition of vectors in terms of arrows.
The dot product of two vectors is the number

Its importance arises from the fact that it is invariant under rotations. To see this, we calculate


According to Pythagoras, the magnitude of  is
is  If we use a different coordinate system, the components of
If we use a different coordinate system, the components of  will be different:
will be different:  But if the new system of axes differs only by a rotation and/or translation of the axes, the magnitude of
But if the new system of axes differs only by a rotation and/or translation of the axes, the magnitude of  will remain the same:
will remain the same:

The squared magnitudes 
 and
and  are invariant under rotations, and so, therefore, is the product
are invariant under rotations, and so, therefore, is the product 
- Show that the dot product is also invariant under translations.
Since by a scalar we mean a number that is invariant under certain transformations (in this case rotations and/or translations of the coordinate axes), the dot product is also known as (a) scalar product. Let us prove that

where  is the angle between
is the angle between  and
and  To do so, we pick a coordinate system
To do so, we pick a coordinate system  in which
in which  In this coordinate system
In this coordinate system  with
with  Since
Since  is a scalar, and since scalars are invariant under rotations and translations, the result
is a scalar, and since scalars are invariant under rotations and translations, the result  (which makes no reference to any particular frame) holds in all frames that are rotated and/or translated relative to
(which makes no reference to any particular frame) holds in all frames that are rotated and/or translated relative to 
We now introduce the unit vectors  whose directions are defined by the coordinate axes. They are said to form an orthonormal basis. Ortho because they are mutually orthogonal:
whose directions are defined by the coordinate axes. They are said to form an orthonormal basis. Ortho because they are mutually orthogonal:

Normal because they are unit vectors:

And basis because every vector  can be written as a linear combination of these three vectors — that is, a sum in which each basis vector appears once, multiplied by the corresponding component of
can be written as a linear combination of these three vectors — that is, a sum in which each basis vector appears once, multiplied by the corresponding component of  (which may be 0):
(which may be 0):

It is readily seen that 

 which is why we have that
which is why we have that

Another definition that is useful (albeit only in a 3-dimensional space) is the cross product of two vectors:

- Show that the cross product is antisymmetric:

As a consequence, 
- Show that

Thus  is perpendicular to both
is perpendicular to both  and
and 
- Show that the magnitude of
 equals
equals  where
where  is the angle between
is the angle between  and
and  Hint: use a coordinate system in which
Hint: use a coordinate system in which  and
and 
Since  is also the area
is also the area  of the parallelogram
of the parallelogram  spanned by
spanned by  and
and  we can think of
we can think of  as a vector of magnitude
as a vector of magnitude  perpendicular to
perpendicular to  Since the cross product yields a vector, it is also known as vector product.
Since the cross product yields a vector, it is also known as vector product.
(We save ourselves the trouble of showing that the cross product is invariant under translations and rotations of the coordinate axes, as is required of a vector. Let us however note in passing that if  and
and  are polar vectors, then
are polar vectors, then  is an axial vector. Under a reflection (for instance, the inversion of a coordinate axis) an ordinary (or polar) vector is invariant, whereas an axial vector changes its sign.)
is an axial vector. Under a reflection (for instance, the inversion of a coordinate axis) an ordinary (or polar) vector is invariant, whereas an axial vector changes its sign.)
Here is a useful relation involving both scalar and vector products:




















































