This Quantum World/Appendix/Relativity/Lorentz contraction time dilation

Lorentz contraction, time dilatation

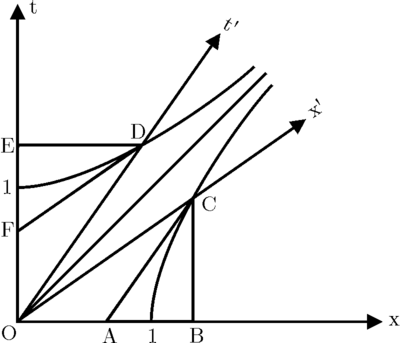
Imagine a meter stick at rest in $\mathcal{F}'.$ At the time $t'=0,$ its ends are situated at the points $O$ and $C.$ At the time $t=0,$ they are situated at the points $O$ and $A,$ which are less than a meter apart. Now imagine a stick (not a meter stick) at rest in $\mathcal{F},$ whose end points at the time $t'=0$ are O and C. In $\mathcal{F}'$ they are a meter apart, but in the stick's rest-frame they are at $O$ and $B$ and thus more than a meter apart. The bottom line: a moving object is contracted (shortened) in the direction in which it is moving.

Next imagine two clocks, one ($\mathcal{C}$) at rest in $\mathcal{F}$ and located at $x=0,$ and one ($\mathcal{C}'$) at rest in $\mathcal{F}'$ and located at $x'=0.$ At $D,$ $\mathcal{C}'$ indicates that one second has passed, while at $E$ (which in $\mathcal{F}$ is simultaneous with $D$), $\mathcal{C}$ indicates that more than a second has passed. On the other hand, at $F$ (which in $\mathcal{F}'$ is simultaneous with $D$), $\mathcal{C}$ indicates that less than a second has passed. The bottom line: a moving clock runs slower than a clock at rest.

Example: Muons ($\mu$ particles) are created near the top of the atmosphere, some ten kilometers up, when high-energy particles of cosmic origin hit the atmosphere. Since muons decay spontaneously after an average lifetime of 2.2 microseconds, they don't travel much farther than 600 meters. Yet many are found at sea level. How do they get that far?

The answer lies in the fact that most of them travel at close to the speed of light. While from its own point of view (that is, relative to the inertial system in which it is at rest), a muon only lives for about 2 microseconds, from our point of view (that is, relative to an inertial system in which it travels close to the speed of light), it lives much longer and has enough time to reach the Earth's surface.