Strength of Materials/General State of Stress

Strength of Materials

Strength of Materials in Engineering Mechanics

Introduction | Introductory Concepts | Loading of Beams | Torsion | General State of Stress | Weakest link determination by use of three parameter Weibull statistics

(last) →  

Principal Stresses

The general state of stress can be represented by a symmetric 3 x 3 matrix.

It is always possible to choose a coordinate system such that all shear stresses are zero. The 3 x 3 matrix is then diagonalised, with the three principal stresses on the diagonal, and all other components equal to zero. The three principal stresses are conventionally labelled σ₁, σ₂ and σ₃.
σ₁ is the maximum (most tensile) principal stress, σ₃ is the minimum (most compressive) principal stress, and σ₂ is the intermediate principal stress.

Stress Invariants

$I_{1}=\sigma _{3}+\sigma _{2}+\sigma _{1}$

$I_{2}=\sigma _{1}\sigma _{2}+\sigma _{2}\sigma _{3}+\sigma _{3}\sigma _{1}$

$I_{3}=\sigma _{1}\sigma _{2}\sigma _{3}$

Hydrostatic Stress

The so-called hydrostatic stress, σ_h, is given by:

$\sigma _{h}=\left.{\frac {\sigma _{1}+\sigma _{2}+\sigma _{3}}{3}}\right.$

Deviatoric Stresses

normal stress - pressure

where pressure = average stress

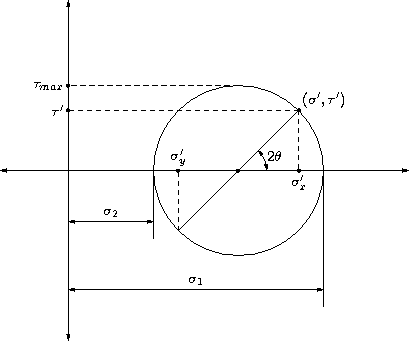
Mohr's Circle

Consider the two dimensional stress condition where the stresses are σ_x, σ_y, and τ_xy. We have, for another set of orthogonal axes x'-y' at angle θ with x-y, the stresses are

$\sigma _{x'}={\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\theta +\tau \sin 2\theta$

$\tau _{x'y'}=-{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\theta +\tau _{xy}\cos 2\theta$

From the above equations, we can see that for any stress states given by σ_x, σ_y, and τ_xy, we can find a value of θ such that the value of σ_x' is maximum. This value is called the principal stress σ₁ (for maximum) or σ₂ (for minimum).

The principal stresses are given by

$\sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

and the maximum shear stress is given by

τ_max = (σ₁ − σ₂)/2

From the definitions for σ_x' and τ_x'y', we have

$\left(\sigma _{x'}-{\frac {\sigma _{x}+\sigma _{y}}{2}}\right)^{2}+\tau _{x'y'}^{2}=\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}$

In the σ-τ graph, this is a circle with center on the x axis, and the distance of the center from the origin is given by (σ_x + σ_y)/2 and a radius given by

$R={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

This circle is known as Mohr's circle, and is useful for visualizing the stress state at a point.

The above figure shows Mohr's circle for a stress state (σ, τ). The center and radius of the circle are obtained from equations stated above. The other stress σ_y can be read off by the point diametrically opposite the (σ, τ) point. The stress at any plane can be found using simple geometrical constructs.

Mohr's Circle for Common Cases

The above shear stress in this case is σ₁/2.

A liquid is one which by definition cannot take a shear. Thus the Mohr-circle diagram is just a point. (The dot should be on the negative side of the axis as the liquids can resist only compression)

For pure shear, the Mohr circle is centered at the origin.

Failure Criteria

In the case of isotropic materials, the state of stress at any point of the body is completely defined by the triad of the principal stresses.

Now that we are able to transform stresses to get the principal stresses, we can use these stresses to consider some of the criteria (theories) postulated for the failure of materials in two- and three-axial states of stress usually based on experiments on yielding and fracture of materials in the uniaxial state of stress. According to such experiments, the kind of failure depends on the type of material. Failure of ductile materials (most of metals) occurs when the elastic limit is reached and yielding commences. Failure of non-ductile materials (e.g., cast iron, concrete) occurs by brittle fracture.

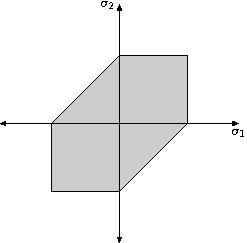
Maximum Shear Stress Criterion

For ductile materials, one failure theory is that of maximum shear stress. We know that the maximum shear stress is given by τ_max = (σ₁ − σ₂)/2. The yield stress, σ_y can be determined by uniaxial tensile tests. Thus, if the maximum shear stress theory is valid, failure occurs when the maximum shear stress reaches σ_y/2.

In the above image, the material will fail if the stress state is outside the shaded region.

Maximum Distortion Energy Criterion

If the maximum shear stress theory is valid, failure occurs when the maximum shear stress reaches ${\frac {{\sqrt {2}}\sigma _{y}}{3}}$.

Failure of Materials

The actual failure mode of each material is unique, though certain criteria can be applied to classes of materials. mode of failure . fatigue failure,