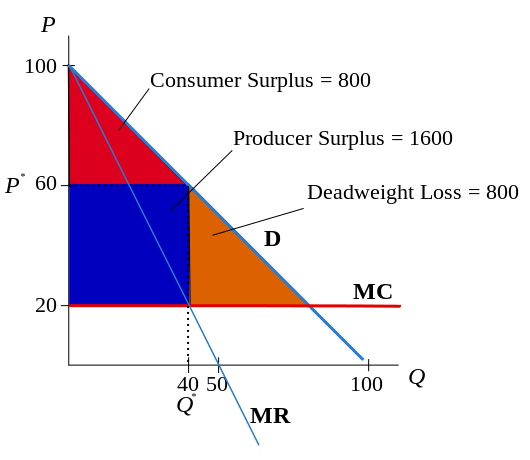Strategy for Information Markets/Background/Self assessment
Quiz #1 (Self-Assessment)
Questions #1 and #2, Supply and Demand
[edit | edit source]1. Demand is given by . Supply is given by . Draw supply and demand, and solve graphically and algebraically for equilibrium price and quantity.
- Algebraically, we can solve for the two quantities being equal: .
- Then, the equilibrium quantity can come out of either the demand or supply function: .
2. Suppose supply decreases so that . Draw the shift in supply and solve graphically and algebraically for the new equilibrium price and quantity.
- To draw, shift the supply curve by noticing that the new supply curve has the same slope as the old one (3, or 1/3 depending on perspective) and solving to find the new intercept at .
- Algebraically: .
- .
Questions #3 and #4, Monopoly Pricing
[edit | edit source]3. Suppose there is a monopolist facing the demand given by , and cost of production is . Find marginal revenue (MR) and marginal cost (MC). Draw the monopolist’s decision problem and solve graphically and numerically for the profit-maximizing quantity and price.
- Revenue is simply price times quantity, but there's a hitch. Since we want to find marginal revenue, that is the change in revenue from an increase in quantity, we need the revenue function to be in terms of quantity, not in terms of price. So, the first thing is to take the demand function and turn it into the inverse demand function .
- Then .
- Marginal revenue is the derivative with respect to quantity: .
- Marginal cost is similarly the derivative of total cost with respect to quantity: .
- Solving algebraically, the monopolist maximizes profit where
- To get a quantity of 40, we look back at the inverse demand function to find the price, and the monopolist sets a price of .
4. On the graph, identify the producer’s surplus, the consumer’s surplus, and the deadweight loss. How much is each?
Questions #5 and #6, Expected Utility
[edit | edit source]5. Suppose that Anne has a utility of money (in dollars) given by . What is her utility for a lottery ticket which pays $100 with probability 1/5, and otherwise nothing?
6. What is the most money Anne would pay for a gamble which pays $36 with probability 2/3, and $81 with probability 1/3?
- .
- So the utility of the gamble is 7, but that's not in dollars. A utility of 7 can come from a variety of gambles, or from a sure thing of .
- The gamble is worth $49 to Anne. That's called the certainty equivalent of the gamble. Since it's worth $49, that's also the most Anne would be willing to pay for the gamble.