Special Relativity/Simultaneity, time dilation and length contraction

More about the relativity of simultaneity

Most physical theories assume that it is possible to synchronise clocks. If you set up an array of synchronised clocks over a volume of space and take a snapshot of all of them simultaneously, you will find that the one closest to you will appear to show a later time than the others, due to the time light needs to travel from each of the distant clocks towards you. However, if the correct clock positions are known, by taking the transmission time of light into account, one can easily compensate for the differences and synchronise the clocks properly. The possibility of truly synchronising clocks exists because the speed of light is constant and this constant velocity can be used in the synchronisation process (the use of the predictable delays when light is used for synchronising clocks is known as "Einstein synchronisation").

The Lorentz transformation for time compares the readings of synchronised clocks at any instant. It compares the actual readings on clocks allowing for any time delay due to transmitting information between observers and answers the question "what does the other observer's clock actually read now, at this moment". The answer to this question is shocking. The Lorentz transformation for time shows that the clocks in any frame of reference moving relative to you cease to be synchronised!

The desynchronisation between relatively moving observers is illustrated below with a simpler diagram:

The effect of the relativity of simultaneity is for each observer to consider that a different set of events is simultaneous. The relativistic phase difference between clocks ("relativistic phase") means that observers who are moving relative to each other have different sets of things that are simultaneous, or in their "present moment". It is this discovery that time is no longer absolute that profoundly unsettles many students of relativity.

The amount by which the clocks differ between two observers depends upon the distance of the clock from the observer ($t=xv/c^{2}$). Notice that if both observers are part of inertial frames of reference with clocks that are synchronised at every point in space then the phase difference can be obtained by simply reading the difference between the clocks at the distant point and clocks at the origin. This difference will have the same value for both observers.

Example: flashing lights

Two lights that are stationary with respect to each other are separated by 3000 metres. The lights flash one after another with a time interval of 4 microseconds between the flashes. How fast would you need to travel along the line of the lights to see the lights flashing simultaneously?

This problem is a straightforward example of relativistic phase, events that are simultaneous for a moving observer being successive events in their own frame of reference. The phase difference between clocks with distance is given by:

Two successive flashes

$\Delta t=vx/c^{2}$

So $v=\Delta tc^{2}/x$

Dividing by $c$ to express $v$ as a fraction of the speed of light gives:

$v_{c}=\Delta tc/x$

Therefore: $v_{c}={\frac {4\times 10^{-6}\times 3\times 10^{8}}{3\times 10^{3}}}$

Thus $v_{c}=0.4c$

(See the "explosion" example in Scherr et al. (2001))

Discuss the relationship between the times that a stationary and a moving observer will assign to the flashes in the example: the Lorentz transformation for the time of an event is $t'=\gamma (t-vx/c^{2})$, it is composed of an elapsed time, $t$ and a phase difference, $vx/c^{2}$. The flashing lights example is arranged so that $t=t'=0$ when the observers in the two inertial frames of reference pass each other at the first flash and so that $t=t$ and $t'=0$ is the time of the second flash.

If $t'=0$ then $0=\gamma (t-vx/c^{2})$ so, according to the Lorentz transformation the moving observer finds events to be simultaneous in the stationary inertial reference frame when $t=vx/c^{2}$, ie: when the elapsed time in the stationary frame is equal to the phase difference between the frames.

Scherr, R.E., Shaffer, P.S. and Vokos, S. Student understanding of time in special relativity: simultaneity and reference frames. Physics Education Research, American Journal of Physics Supplement, 69, S24-35 (2001)

Example: Relativistic Bug Capture

How fast would a 1000 m long spaceship need to travel to observe a nanosecond difference between stationary clocks aligned with its bow and stern?

From $t=xv/c^{2}$:

$10^{-9}=10^{3}v/(9\times 10^{16})$

Therefore $v=9\times 10^{4}ms^{-1}$ or 90 km per second.

This effect could be used to bring together bugs of different ages that are twins in their own inertial frame of reference:

Bill travels past Jim in a very long spaceship and simultaneously captures two bugs, one coincident with the bow of the spaceship and one coincident with the stern. Although the bugs are twins in their own frame of reference they are different ages in Bill's reference frame. The captured bugs are free to wander up and down Bill's spaceship and could meet each other.

What length of spaceship travelling at 90 km per second would be needed to capture the bugs in the picture?

The Andromeda Paradox

What do we mean when we say that events are occurring "now"? If we are looking out over a cityscape, watching the traffic, lots of things appear to be happening all at once. We can take a snapshot with a camera and the scene on the photo consists of all those things that happened at very nearly the same time. They are only "very nearly" at the same time because the events on the photo that were furthest away actually occurred slightly earlier than those that were nearby because of the time taken for light to reach the camera. If we want to discover the events that really happened at the same time we would need to subtract the time taken for the light to get to us. This would be highly necessary if you were observing events on the Moon: if you were on the Earth and saw the time on a lunar clock you would know that the real time on the moon was more than a second later. But would this be enough? What about the relativistic phase differences between clocks due to motion?

Special Relativity introduces yet another factor, in addition to the travel time of light, that upsets our knowledge of which events are simultaneous. The relativistic phase differences between clocks are tiny at the distance of the moon but have the startling consequence that at distances as large as our separation from nearby galaxies an observer who is driving on the earth can have a radically different set of events that are simultaneous with her "present moment" from another person who is standing on the earth. The classic example of this effect of relativistic phase is the "Andromeda Paradox", also known as the "Rietdijk-Putnam-Penrose" argument. Penrose described the argument:

"Two people pass each other on the street; and according to one of the two people, an Andromedean space fleet has already set off on its journey, while to the other, the decision as to whether or not the journey will actually take place has not yet been made. How can there still be some uncertainty as to the outcome of that decision? If to either person the decision has already been made, then surely there cannot be any uncertainty. The launching of the space fleet is an inevitability." (Penrose 1989).

The argument is illustrated below:

Notice that neither observer can actually "see" what is happening on Andromeda now. The argument is not about what can be "seen", it is purely about what different observers consider to be contained in their instantaneous present moment. The two observers observe the same, two million year old events in their telescopes but the moving observer must assume that events at the present moment on Andromeda are a day or two in advance of those in the present moment of the stationary observer. (Incidentally, the two observers see the same events in their telescopes because length contraction of the distance from Earth to Andromeda compensates exactly for the time difference on Andromeda.)

This "paradox" has generated considerable philosophical debate on the nature of time and free-will. The advanced text of this book provides a discussion of some of the issues surrounding this geometrical interpretation of special relativity.

A result of the relativity of simultaneity is that if the car driver launches a space rocket towards the Andromeda galaxy it might have a several days head start compared with a space rocket launched from the ground. This is because the "present moment" for the moving car driver is progressively advanced with distance compared with the present moment on the ground. The present moment for the car driver is shown in the illustration below:

The net effect of the Andromeda paradox is that when someone is moving towards a distant point there are later events at that point than for someone who is not moving towards the distant point. There is a time gap between the events in the present moment of the two people.

The twin paradox

The "Twin Paradox" derives from an article by Langevin (1911) who used travel to a distant star and back to describe the relationships between times in different inertial reference frames. Langevin's original example was called the "Clock Paradox" and showed that a space traveller who travels to a distant star and back finds that he has aged less than the people who stay on Earth. Benguigui (2012) provides a detailed account of how, over time, this example became the story of two twins, one who travels out into space and one who stays at home, and how it became described by Weyl in 1922 as the "Twin Paradox". The "Twin Paradox" is an interesting example of the relativity of simultaneity and time dilation and deserves close study so that these features of Special Relativity can be understood. However, be warned, the reason that the "twin paradox" has attracted so much puzzlement is that, although superficially a simple problem, the analysis of the various inertial frames of reference is complex.

A one way trip

The twin "paradox" consists of two journeys, an outbound journey and a return journey. Much can be learnt about the relativity of simultaneity by considering just the outbound journey without any return. The single journey without any return might consist of the following scenario: Jim stays at home on Earth and Bill goes off in a spaceship, Bill flies past Jim at a velocity of 0.8c, they both set all of their clocks to zero as they pass each other and Bill flies straight to Mars where he drops off a record of his clock reading. Jim, who stays on Earth, finds that Bill's clocks record less time than his own for the journey.

The journey to Mars consists of two inertial frames of reference. In Jim's frame of reference Bill is moving and Jim is stationary. In Bill's frame of reference Jim, Earth and Mars move and Bill is stationary. There are only two reference frames so questions such as "what does Jim observe if he considers himself to be moving" are equivalent to asking "how does Jim move in Bill's frame of reference?".

The start of the journey is shown below:

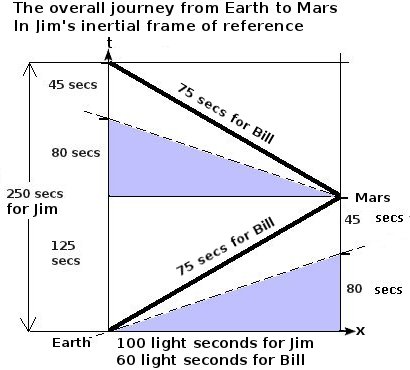
Suppose for ease of calculation Mars is assumed to be 100 light seconds away from Earth. Jim's view of the journey is straightforward and is shown below:

If Mars is 100 light seconds away, Jim will time Bill's journey to take 125 seconds ($100/0.8$). Relativistic time dilation will cause Bill's clocks to read 75 seconds ie:

Bill's clocks will read: $125/\gamma$

where gamma is: ${\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=1.667$

so $125/1.6667=75$ seconds.

In Jim's inertial frame of reference Jim has aged by 125 seconds when Bill gets to Mars but Bill, as a result of time dilation, has only aged by 75 seconds.

The reason that this lack of aging by Bill seems to be paradoxical is that it might be thought that Jim must also have aged less than Bill, after all, Jim travels away from Bill as much as Bill travels away from Jim so Bill should find Jim to have aged less than himself in the same way as Jim finds Bill to have aged less than himself. In fact there is no paradox because Bill and Jim have very different ideas of the journey. Bill's view of the journey is shown below.

As a result of relativistic phase, Bill finds that the clocks on Mars start the journey 80 seconds ahead of his own. The Martian clocks record another 45 seconds for the journey. The 45 seconds elapsed time for the journey is what Bill expects when time dilation is taken into account (ie: $75/\gamma =75/1.6667=45$ seconds). More surprising still, when Bill considers Jim's clock readings back on Earth he finds that only 45 seconds have elapsed on Jim's earth-based clocks during the journey because the 80 seconds of relativistic phase difference mean that Bill's clocks as he passes Mars are simultaneous with events on Earth that are only 45 seconds later than when he passed Earth.

If Bill had an absurdly long rocket he could use a version of "relativistic bug capture" (see above) to net one of Jim's clocks the moment Bill reaches Mars. Bill could then show there was a Jim on Earth whose clocks had only progressed by 45 seconds for Bill's journey in Bill's inertial frame of reference. If Bill had captured one of Jim's clocks, the Jim who is simultaneous in his own frame of reference with the moment that Bill passes Mars would remember a giant net coming down from the tail of a spaceship and taking one of his clocks 45 seconds after Bill passed him.

Notice that there are two Jims in this story, one who is simultaneous with the Mars that Bill visits and another who is simultaneous with Bill in Bill's frame of reference. The Jim who is simultaneous with Bill in Bill's frame of reference would be an earlier Jim than the Jim who is simultaneous in his own frame of reference with Mars when Bill arrives.

The one way journey is symmetrical in the sense that Jim observes Bill to age less than himself during the journey and Bill also observes an earlier Jim to have aged less than himself.

The one way journey would become fully symmetrical if Bill continued past Mars until his clocks read that 125 seconds had elapsed, at this point he would assess that Jim had experienced 75 seconds of elapsed time. When Jim's clock's read 125 seconds Jim finds Bill's clocks read 75 seconds and, symmetrically, when Bill's clocks read 125 seconds Bill finds that Jim's clocks read 75 seconds. This symmetry is emphasised in the schematic diagram below which compares Jim and Bill's clock readings:

What happens when there is a change of velocity?

In the previous section it was shown that time dilation is symmetrical when observers separate at a constant velocity. The symmetry is evident in the way that, during the one way journey, Jim observes Bill's clocks to go slow and Bill also observes Jim's clocks to go slow. The symmetry between the observers means that Bill can regard himself as stationary and observing Jim departing or vice versa.

Bill finds that there are two Jims at two separate times involved in going to Mars then suddenly changing direction to return to Earth: these are labelled A and C in the diagram. The first Jim has clocks that read 45 seconds since Bill passed Earth, this is the Jim who is simultaneous with Bill in Bill's frame of reference as Bill passes Mars. The second Jim has clocks that read 205 seconds since meeting Bill, this Jim is simultaneous with Bill, in Bill's frame of reference, the moment after he has turned around at Mars and reached a velocity of -0.8c for the return journey.

The lack of any single Jim that is simultaneous with Bill when Bill changes velocity introduces an asymmetry into Special Relativity. Bill turning around at Mars to come back to Earth is not equivalent to Earth turning to meet Bill because it is not clear, until Bill has made the turn, which Earth and which Jim is making the journey. Langevin (1911), who first proposed the example of a traveller departing and returning younger, was well aware of the asymmetry and stated that: "Thus the asymmetry – which occurred because only the traveler, in the middle of his journey, has undergone an acceleration that changes the direction of his velocity".

In Special Relativity the laws of physics are the same for each observer in an inertial frame of reference. An inertial frame of reference might be all the clocks and measuring rods in a room on board a ship or in an entire city, the crucial feature of an inertial reference frame being that the clocks and measuring rods are stationary with respect to each other. Motions are measured so that the rest of the universe moves relative to the observer's inertial frame of reference. There are three inertial frames of reference in the example of Bill going to Mars and returning to Earth: Jim, outbound Bill and inbound Bill. Outbound and inbound Bill are separated by a period of varying velocity when Bill turns around. This period of changing velocity can also be regarded as a non-inertial hiatus in Bill's single inertial reference frame after which the relations between Bill's clocks and measuring rods and those in the rest of the universe have changed.

Questions such as "how does the Jim who is simultaneous with Bill after the turn view events if he regards himself as moving towards Bill?" are really about the inbound Bill's reference frame. In Jim's own inertial frame of reference Bill just goes to Mars, turns round and comes back again. Jim always regards himself as stationary unless his reference frame becomes non-inertial by experiencing a change in velocity in which case Jim would regard himself as moving from one stationary state to another that has a different set of relationships with the universe. Special Relativity holds that the laws of physics are the same in all inertial reference frames, it does not hold that all motion is relative, even in non-inertial changes.

The gap in time between the Jim who is simultaneous with Bill as Bill reaches Mars and the Jim who is simultaneous with Bill as he starts the journey back to Earth is known as the "Time Gap". The time gap in the "twin paradox" consists of the sum of the outgoing and incoming phase differences and in this case the time gap is 160 seconds .

The time gap description of the "twin paradox"

Once it is accepted that Bill and Jim have very different views of the journey these views can be summarised in the "Time Gap" description of the journey. In this description Bill flies to Mars and discovers that the clocks there are reading a later time than his own clock. He turns round to fly back to Earth and realises that the relativity of simultaneity means that, for Bill, the clocks on Earth will have jumped forward and are ahead of those on Mars, yet another "time gap" appears. When Bill gets back to Earth the time gaps and time dilations mean that people on Earth have recorded more clock ticks that he did.

For ease of calculation suppose that Bill is moving at a truly astonishing velocity of 0.8c in the direction of a distant point that is 100 light seconds away (about 30 million kilometres). The illustration below shows Jim and Bill's observations:

From Bill's viewpoint there is both a time dilation and a phase effect. It is the added factor of "phase" that explains why, although the time dilation occurs for both observers, Bill observes the same readings on Jim's clocks over the whole journey as does Jim.

To summarise the mathematics of the twin paradox using the example:

Jim observes the distance as 100 light seconds and the distant point is in his frame of reference. According to Jim it takes Bill the following time to make the journey:

Time taken = distance / velocity therefore according to Jim:

$t=100/0.8=125$ seconds

Again according to Jim, time dilation should affect the observed time on Bill's clocks:

$T=t\times {\sqrt {1-v^{2}/c^{2}}}$ so:

$T=125\times {\sqrt {1-0.8^{2}}}=75$ seconds

So for Jim the round trip takes 250 secs and Bill's clock reads 150 secs.

Bill measures the distance as:

$X=x\times {\sqrt {1-v^{2}/c^{2}}}=100\times {\sqrt {1-0.8^{2}}}=60$ light seconds.

For Bill it takes $X/v=60/0.8=75$ seconds.

Bill observes Jim's clocks to appear to run slow as a result of time dilation:

$t^{'}=T\times {\sqrt {1-v^{2}/c^{2}}}$ so:

$t^{'}=75\times {\sqrt {1-0.8^{2}}}=45$ seconds

But there is also a time gap of $vx/c^{2}=80$ seconds.

So for Bill, Jim's clocks register 125 secs have passed from the start to the distant point. This is composed of 45 secs elapsing on Jim's clocks at the turn round point plus an 80 secs time gap from the start of the journey. Bill sees 250 secs total time recorded on Jim's clocks over the whole journey, this is the same time as Jim observes on his own clocks.

Further reading:

Benguigui, L (2012). A tale of two twins. arXiv:1212.4414v1

Bohm, D. The Special Theory of Relativity (W. A. Benjamin, 1965).

D’Inverno, R. Introducing Einstein’s Relativity (Oxford University Press, 1992).

Eagle, A. A note on Dolby and Gull on radar time and the twin "paradox". American Journal of Physics. 2005, VOL 73; NUMB 10, pages 976-978. http://arxiv.org/PS_cache/physics/pdf/0411/0411008v2.pdf

Langevin, P. (1911) L'Evolution de l'espace et du temps Scientia 10 (1911), 31-34

The nature of length contraction

According to special relativity items such as measuring rods consist of events distributed in space and time and a three dimensional rod is the events that compose the rod at a single instant. However, from the relativity of simultaneity it is evident that two observers in relative motion will have different sets of events that are present at a given instant. This means that two observers moving relative to each other will usually be observing measuring rods that are composed of different sets of events. If the word "rod" means the three dimensional form of the object called a rod then these two observers in relative motion observe different rods.

The way that measuring rods differ between observers can be seen by using a Minkowski diagram. The area of a Minkowski diagram that corresponds to all of the events that compose an object over a period of time is known as the worldtube of the object. It can be seen in the image below that length contraction is the result of individual observers having different sections of an object's worldtube in their present instant.

(It should be recalled that the longest lengths on space-time diagrams are often the shortest in reality).

It is sometimes said that length contraction occurs because objects rotate into the time axis. This is actually a half truth, there is no actual rotation of a three dimensional rod, instead the observed three dimensional slice of a four dimensional rod is changed which makes it appear as if the rod has rotated into the time axis. In special relativity it is not the rod that rotates into time, it is the observer's slice of the worldtube of the rod that rotates.

There can be no doubt that the three dimensional slice of the worldtube of a rod does indeed have different lengths for relatively moving observers. The issue of whether or not the events that compose the worldtube of the rod are always existent is a matter for philosophical speculation.

Further reading:

Vesselin Petkov. (2005) Is There an Alternative to the Block Universe View?

Dragan V Redžić (2010). Relativistic length agony continued

More about time dilation

The term "time dilation" is applied to the way that observers who are moving relative to you record fewer clock ticks between events than you. In special relativity this is not due to properties of the clocks, such as their mechanisms getting heavier. Indeed, it should not even be said that the clocks tick faster or slower because what is truly occurring is that the clocks record shorter or longer elapsed times and this recording of elapsed time is independent of the mechanism of the clocks. The differences between clock readings are due to the clocks traversing shorter or longer distances between events along an observer's path through spacetime. This can be seen most clearly by re-examining the Andromeda Paradox.

Suppose Bill passes Jim at high velocity on the way to Mars. Jim has previously synchronised the clocks on Mars with his Earth clocks but for Bill the Martian clocks read times well in advance of Jim's. This means that Bill has a head start because his present instant contains what Jim considers to be the Martian future. Jim observes that Bill travels through both space and time and expresses this observation by saying that Bill's clocks recorded fewer ticks than his own. Bill achieves this strange time travel by having what Jim considers to be the future of distant objects in his present moment. Bill is literally travelling into future parts of Jim's frame of reference.

In special relativity time dilation and length contraction are not material effects, they are physical effects due to travel within a four dimensional spacetime. The mechanisms of the clocks and the structures of measuring rods are irrelevant.

It is important for advanced students to be aware that special relativity and General Relativity differ about the nature of spacetime. General Relativity, in the form championed by Einstein, avoids the idea of extended space and time and is what is known as a "relationalist" theory of physics. Special relativity, on the other hand, is a theory where extended spacetime is pre-eminent. The brilliant flowering of physical theory in the early twentieth century has tended to obscure this difference because, within a decade, special relativity had been subsumed within General Relativity. The interpretation of special relativity that is presented here should be learnt before advancing to more advanced interpretations.

The Pole-barn paradox

The length contraction in relativity is symmetrical. When two observers in relative motion pass each other they both measure a contraction of length.

(Note that Minkowski's metric involves the subtraction of displacements in time, so what appear to be the longest lengths on a 2D sheet of paper are often the shortest lengths in a (3+1)D reality).

The symmetry of length contraction leads to two questions. Firstly, how can a succession of events be observed as simultaneous events by another observer? This question led to the concept of de Broglie waves and quantum theory. Secondly, if a rod is simultaneously between two points in one frame how can it be observed as being successively between those points in another frame? For instance, if a pole enters a building at high speed how can one observer find it is fully within the building and another find that the two ends of the rod are opposed to the two ends of the building at successive times? What happens if the rod hits the end of the building? The second question is known as the "pole-barn paradox" or "ladder paradox".

The pole-barn paradox states the following: suppose a superhero running at 0.75c and carrying a horizontal pole 15 m long towards a barn 10m long, with front and rear doors. When the runner and the pole are inside the barn, a ground observer closes and then opens both doors (by remote control) so that the runner and pole are momentarily captured inside the barn and then proceed to exit the barn from the back door.

One may be surprised to see a 15-m pole fit inside a 10-m barn. But the pole is in motion with respect to the ground observer, who measures the pole to be contracted to a length of 9.9 m (check using equations).

The “paradox” arises when we consider the runner’s point of view. The runner sees the barn contracted to 6.6 m. Because the pole is in the rest frame of the runner, the runner measures it to have its proper length of 15 m. Now, how can our superhero make it safely through the barn?

The resolution of the “paradox” lies in the relativity of simultaneity. The closing of the two doors is measured to be simultaneous by the ground observer. However, since the doors are at different positions, the runner says that they do not close simultaneously. The rear door closes and then opens first, allowing the leading edge of the pole to exit. The front door of the barn does not close until the trailing edge of the pole passes by.

What happens if the rear door is kept closed and made out of some impenetrable material? Can we or can we not trap the rod inside the barn by closing the front door while the whole rod is inside according to a ground observer? When the front end of the rod hits the rear door, information about this impact will travel backwards along the rod in the form of a shock wave. The information cannot travel faster than c, so the rear end of the rod will continue to travel forward at its original speed until the wave reaches it. Even if the shock wave is traveling at the speed of light, it will not reach the rear end of the rod until after the rear end has passed through the front door even in the runner's frame. Therefore the whole rod (albeit quite scrunched up) will be inside the barn when the front door closes. If it is infinitely elastic, it will end up compressed and "spring loaded" against the inside of the closed barn.

Evidence for length contraction, the field of an infinite straight current

Length contraction can be directly observed in the field of an infinitely straight current. This is shown in the illustration below.

Non-relativistic electromagnetism describes the electric field due to a charge using:

$E={\frac {\lambda }{2\pi \epsilon _{0}r}}$

and describes the magnetic field due to an infinitely long straight current using the Biot Savart law:

$B={\frac {\mu _{0}I}{2\pi r}}$

Or using the charge density (from $I=\lambda v$ where $\lambda$ is the amount of charges per unit length):

$B={\frac {\mu _{0}\lambda v}{2\pi r}}$

Using relativity it is possible to show that the formula for the magnetic field given above can be derived using the relativistic effect of length contraction on the electric field and so what we call the "magnetic" field can be understood as relativistic observations of a single phenomenon. The relativistic calculation is given below.

If Jim is moving relative to the wire at the same velocity as the negative charges he sees the wire contracted relative to Bill:

$l_{+}=l{\sqrt {1-v^{2}/c^{2}}}$

Bill should see the space between the charges that are moving along the wire to be contracted by the same amount but the requirement for electrical neutrality means that the moving charges will be spread out to match those in the frame of the fixed charges in the wire.

This means that Jim sees the negative charges spread out so that:

$l_{-}={\frac {l}{\sqrt {1-v^{2}/c^{2}}}}$

The net charge density observed by Jim is:

$\lambda ={\frac {q}{l_{-}}}-{\frac {q}{l_{+}}}$

Substituting:

$\lambda ={\frac {q}{l}}({\sqrt {1-v^{2}/c^{2}}}-{\frac {1}{\sqrt {1-v^{2}/c^{2}}}})$

Using the binomial expansion:

$\lambda ={\frac {q}{l}}(1-{\frac {v^{2}}{2c^{2}}}-1-{\frac {v^{2}}{2c^{2}}})$

Therefore, allowing for a net positive charge, the positive charges being fixed:

$\lambda ={\frac {qv^{2}}{lc^{2}}}$

The electric field at Jim's position is given by:

$E={\frac {\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

The force due to the electrical field at Jim's position is given by $F=Eq$ which is:

$F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

Now, from classical electromagnetism:

$c^{2}={\frac {1}{\epsilon _{0}\mu _{0}}}$

So substituting this into $F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$:

(1) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

This is the formula for the relativistic electric force that is observed by Bill as a magnetic force. How does this compare with the non-relativistic calculation of the magnetic force? The force on a charge at Jim's position due to the magnetic field is, from the classical formula:

$F=Bqv$

Which from the Biot-Savart law is:

(2) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

which shows that the same formula applies for the relativistic excess electrical force experienced by Jim as the formula for the classical magnetic force.

It can be seen that once the idea of space-time is understood the unification of the two fields is straightforward. Jim is moving relative to the wire at the same speed as the negatively charged current carriers so Jim only experiences an electric field. Bill is stationary relative to the wire and observes that the charges in the wire are balanced whereas Jim observes an imbalance of charge. Bill assigns the attraction between Jim and the current carriers to a "magnetic field".

It is important to notice that, in common with the explanation of length contraction given above, the events that constitute the stream of negative charges for Jim are not the same events as constitute the stream of negative charges for Bill. Bill and Jim's negative charges occupy different moments in time.

Incidently, the drift velocity of electrons in a wire is about a millimetre per second but a huge charge is available in a wire (See link below).

Further reading:

Purcell, E. M. Electricity and Magnetism. Berkeley Physics Course. Vol. 2. 2nd ed. New York, NY: McGraw-Hill. 1984. ISBN: 0070049084.

Useful links:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmmic.html

http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/releng.html

De Broglie waves

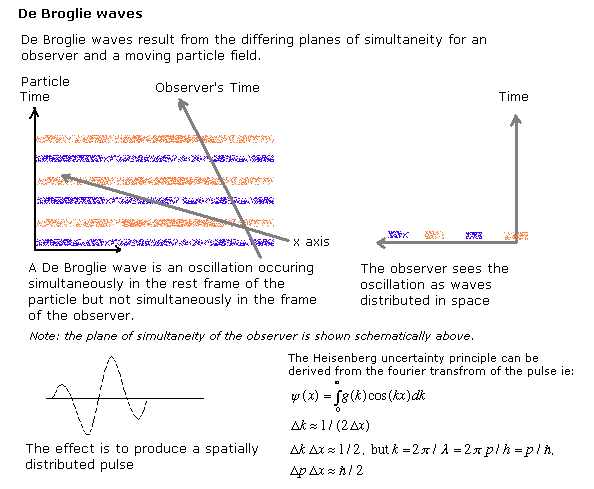
De Broglie noticed that the differing three dimensional sections of the universe would cause oscillations in the rest frame of an observer to appear as wave trains in the rest frame of observers who are moving.

He combined this insight with Einstein's ideas on the quantisation of energy to create the foundations of quantum theory. De Broglie's insight is also a round-about proof of the description of length contraction given above - observers in relative motion have differing three dimensional slices of a four dimensional universe. The existence of matter waves is direct experimental evidence of the relativity of simultaneity.

Further reading: de Broglie, L. (1925) On the theory of quanta. A translation of : RECHERCHES SUR LA THEORIE DES QUANTA (Ann. de Phys., 10e s´erie, t. III (Janvier-F ´evrier 1925).by: A. F. Kracklauer. http://replay.web.archive.org/20090509012910/http://www.ensmp.fr/aflb/LDB-oeuvres/De_Broglie_Kracklauer.pdf

Bell's spaceship paradox

Bell devised a thought experiment called the "Spaceship Paradox" to enquire whether length contraction involved a force and whether this contraction was a contraction of space. In the Spaceship Paradox two spaceships are connected by a thin, stiff string and are both equally and linearly accelerated to a velocity $v$ relative to the ground, at which, in the special relativity version of the paradox, the acceleration ceases. The acceleration on both spaceships is arranged to be equal according to ground observers so, according to observers on the ground, the spaceships will stay the same distance apart. It is asked whether the string would break.

It is useful when considering this problem to investigate what happens to a single spaceship. If a spaceship that has rear thrusters is accelerated linearly, according to ground observers, to a velocity $v$ then the ground observers will observe it to have contracted in the direction of motion. The acceleration experienced by the front of the spaceship will have been slightly less than the acceleration experienced by the rear of the spaceship during contraction and then would suddenly reach a high value, equalising the front and rear velocities, once the rear acceleration and increasing contraction had ceased. From the ground it would be observed that overall the acceleration at the rear could be linear but the acceleration at the front would be non-linear.

In Bell's thought experiment both spaceships are artificially constrained to have constant acceleration, according to the ground observers, until the acceleration ceases. Sudden adjustments are not allowed. Furthermore no difference between the accelerations at the front and rear of the assembly are permitted so any tendency towards contraction would need to be borne as tension and extension in the string.

The most interesting part of the paradox is what happens to the space between the ships. From the ground the spaceships will stay the same distance apart (the experiment is arranged to achieve this) whilst according to observers on the spaceships they will appear to become increasingly separated. This implies that acceleration is not invariant between reference frames (see Part II) and the force applied to the spaceships will indeed be affected by the difference in separation of the ships observed by each frame.

The section on the nature of length contraction above shows that as the string changes velocity the observers on the ground observe a changing set of events that compose the string. These new events define a string that is shorter than the original. This means that the string will indeed attempt to contract as observed from the ground and will be drawn out under tension as observed from the spaceships. If the string were unable to bear the extension and tension in the moving frame or the tension in the rest frame it would break.

Another interesting aspect of Bell's Spaceship Paradox is that in the inertial frames of the ships, owing to the relativity of simultaneity, the lead spaceship will always be moving slightly faster than the rear spaceship so the spaceship-string system does not form a true inertial frame of reference until the acceleration ceases in the frames of reference of both ships. The asynchrony of the cessation of acceleration shows that the lead ship reaches the final velocity before the rear ship in the frame of reference of either ship. However, this time difference is very slight (less than the time taken for an influence to travel down the string at the speed of light $x/c>vx/c^{2}$).

It is necessary at this stage to give a warning about extrapolating special relativity into the domain of general relativity (GR). SR cannot be applied with confidence to accelerating systems which is why the comments above have been confined to qualitative observations.

Further reading

Bell, J. S. (1976). Speakable and unspeakable in quantum mechanics. Cambridge University Press 1987 ISBN 0-521-52338-9

Hsu, J-P and Suzuki, N. (2005) Extended Lorentz Transformations for Accelerated Frames and the Solution of the “Two-Spaceship Paradox” AAPPS Bulletin October 2005 p.17 http://www.aapps.org/archive/bulletin/vol15/15-5/15_5_p17p21%7F.pdf

Matsuda, T and Kinoshita, A (2004. A Paradox of Two Space Ships in Special Relativity. AAPPS Bulletin February 2004 p3. http://www.aapps.org/archive/bulletin/vol14/14_1/14_1_p03p07.pdf

The transverse doppler effect

The existence of time dilation means that the frequency of light emitted from a source that is moving towards or away from an observer should be red shifted in directions that are perpendicular to the direction of motion. The transverse doppler effect is given by:

$\nu =\nu ^{\prime }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

Where $\nu$ is the observed frequency and $\nu ^{\prime }$ is the frequency if the source were stationary relative to the observer (the proper frequency).

This effect was first confirmed by Ives and Stillwell in 1938. The transverse doppler effect is a purely relativistic effect and has been used as an example of proof that time dilation occurs.

Relativistic transformation of angles

If a rod makes an angle with its direction of motion toward or away from an observer the component of its length in the direction of motion will be contracted. This means that observed angles are also transformed during changes of frames of reference. Assuming that motion occurs along the x-axis, suppose the rod has a proper length (rest length) of $L^{\prime }$ metres and makes an angle of $\theta ^{\prime }$degrees with the x'-axis in its rest frame. The tangent of the angle made with the axes is:

Tangent in rest frame of rod = $\tan \theta ^{\prime }={\frac {L_{y}^{\prime }}{L_{x}^{\prime }}}$

Tangent in observer's frame = $\tan \theta ={\frac {L_{y}}{L_{x}}}$

Therefore:

${\frac {\tan \theta }{\tan \theta ^{\prime }}}={\frac {L_{y}L_{x}^{\prime }}{L_{y}^{\prime }L_{x}}}$

But $L_{x}=L_{x}^{\prime }{\sqrt {1-v^{2}/c^{2}}}$

And $L_{y}=L_{y}^{\prime }$

So

$\tan \theta ={\frac {\tan \theta ^{\prime }}{\sqrt {1-v^{2}/c^{2}}}}$

Showing that angles with the direction of motion are observed to increase with velocity.

The angle made by a moving object with the x-axis also involves a transformation of velocities to calculate the correct angle of incidence.

Addition of velocities

How can two observers, moving at v m/sec relative to each other, compare their observations of the velocity of a third object?

Suppose one of the observers measures the velocity of the object as $u^{'}$ where:

$u^{'}={\frac {x^{'}}{t^{'}}}$

The coordinates $x^{'}$ and $t^{'}$ are given by the Lorentz transformations:

$x^{'}={\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}$

and

$t^{'}={\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

but

$x^{'}=u^{'}t^{'}$

so:

${\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}=u^{'}{\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

and hence:

$x-vt=u^{'}(t-vx/c^{2})$

Notice the role of the phase term $vx/c^{2}$. The equation can be rearranged as:

$x={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}t$

given that $x=ut$:

$u={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}$

This is known as the relativistic velocity addition theorem, it applies to velocities parallel to the direction of mutual motion.

The existence of time dilation means that even when objects are moving perpendicular to the direction of motion there is a discrepancy between the velocities reported for an object by observers who are moving relative to each other. If there is any component of velocity in the x direction (${u_{x}}$, ${{u^{'}}_{x}}$) then the phase affects time measurement and hence the velocities perpendicular to the x-axis. The table below summarises the relativistic addition of velocities in the various directions in space.

${u^{'}}_{x}={\frac {(u_{x}-v)}{(1-u_{x}v/c^{2})}}$	$u_{x}={\frac {({u^{'}}_{x}+v)}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{y}={\frac {u_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{y}={\frac {{u^{'}}_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{z}={\frac {u_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{z}={\frac {{u^{'}}_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}</P>$

Notice that for an observer in another reference frame the sum of two velocities (u and v) can never exceed the speed of light. This means that the speed of light is the maximum velocity in any frame of reference.