Special Relativity/Problems
Jump to navigation
Jump to search
Problems
[edit | edit source]- Sketch your personal world line on a spacetime diagram for the last 24 hours, labeling by time and location special events such as meals, physics classes, etc. Relate the slope of the world line at various times to how fast you were walking, riding in a car, etc.
- Spacetime conversions:
- What is the distance from New York to Los Angeles in seconds? From here to the moon? From here to the sun?
- What is one nanosecond in meters? One second? One day? One year?
- Three events have the following spacetime coordinates: A is at ; B is at ; C is at .
- A world line for an object passes through events B and C. How fast and in which direction is the object moving?
- A line of simultaneity for a coordinate system passes through events A and B. How fast and in which direction is the coordinate system moving?
- What is the invariant interval between events A and B? B and C? A and C?
- Can a signal from event B reach event A? Can it reach event C? Explain.
Hint: Draw a spacetime diagram with all the events plotted before trying to answer the above questions.
- In the following problem be sure to indicate the slope of on pertinent lines drawn.
- In a spacetime diagram, sketch a line of simultaneity for a reference frame moving to the left at , where is the speed of light.
- Sketch the world line of an object which is initially stationary, but which accelerates to a velocity of .
- Suppose that an interstellar spaceship goes a distance relative to the rest frame in of its own time.
- Draw a spacetime diagram in the rest frame showing , , and the time needed for this journey relative to the rest frame.
- Cmpute , using your spacetime diagram as an aid.
- Compute the speed of the spaceship.
- If an airline pilot flies per month (in the rest frame) at for , how much younger will she be than her twin brother (who handles baggage) when she retires? Hint: Use for small .
- A mu particle normally lives about before it decays. However, muons created by cosmic rays up in the atmosphere reach the Earth's surface. How fast must they be going?
- The Stanford Linear Accelerator accelerates electrons to a speed such that the long accelerator appears to be long to the electron, due to the Lorentz contraction. How much less than the speed of light is the electron traveling? Hint: It is best to first develop an approximation for the relationship between and the difference between and for a particle moving close to the speed of light.
- How fast do you have to go to reach the center of our galaxy in your expected lifetime? At this speed, what does this distance appear to be? (We are about from the galactic center.)
- Two identical spaceships pass each other going in the opposite direction at the same speed.
- Sketch a spacetime diagram showing the world lines of the front and rear of each spaceship.
- Indicate an interval on the diagram corresponding to the rightward-moving spaceship's length in its own reference frame.
- Indicate an interval corresponding to the leftward-moving spaceship's length in the reference frame of the rightward-moving spaceship.
- Indicate an interval equal to the length of either spaceship in the rest frame.
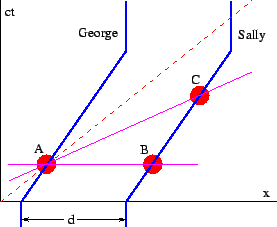
- George and Sally are identical twins initially separated by a distance and at rest. In the rest frame they are initially the same age. At time both George and Sally get in their spaceships and head to the right at velocity . Both move a distance to the right and decelerate to a halt. (See figure 4.10.)
- When both are moving, how far away is Sally according to George?
- How much older or younger is Sally relative to George while both are moving?
- How much older or younger is Sally relative to George after both stop?
Hint: Draw the triangle ABC in a reference frame moving with George and Sally.