Special Relativity/Principle of Relativity

From Wikibooks, the open-content textbooks collection

Jump to: navigation, search
Special Relativity

Contents

[edit] The principle of relativity

Galileo Galilei

Principles of relativity address the relationship between observations made at different places. This problem has been a difficult theoretical challenge since the earliest times and involves physical questions such as how the velocities of objects can be combined and how influences are transmitted between moving objects.

Galileo (1632), in his "Dialogue Concerning the Two Chief World Systems", considered observations of motion made by people inside a ship who could not see the outside:

"have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still. "

According to Galileo, if the ship moved smoothly someone inside it would be unable to determine whether they were moving. This concept led to Galilean Relativity in which it was held that things continue in a state of motion unless acted upon. This simple idea challenged the previous ideas of Aristotle. Aristotle had argued in his "Physics" that things must either be moved or be at rest. According to Aristotle, on the basis of complex and interesting arguments about the possibility of a 'void', things cannot remain in a state of motion without something moving them. As a result Aristotle proposed that objects would stop entirely in empty space. Aristotle's idea had been believed by everyone so Galileo's new proposal was extraordinary and, because it was nearly right, became the foundation of physics.

Galilean Relativity contains two important principles: firstly it is impossible to determine who is actually at rest and secondly things continue in uniform motion unless acted upon. The second principle is known as Galileo’s Law of Inertia or Newton's First Law of Motion.

Reference:

[edit] Special relativity

Until the nineteenth century it appeared that Galilean relativity treated all observers as equivalent. According to Galilean Relativity, if an observer launches a vessel containing another observer at a thousand kilometres per hour and the second observer launches another vessel containing a third observer in the same direction at a thousand kilometres per hour then the third observer will calculate that it is going at two thousand kilometres per hour relative to the first observer. This linear addition of velocities means that all observers would be equivalent.

This simple scheme became questioned in 1865 when James Clerk Maxwell discovered the equations that describe the propagation of electromagnetic waves such as light. One of his equations determines the velocity of light based on constants called the permittivity and permeability of the medium through which it travels. These constants were thought to be simple properties of a physical medium or “aether” that pervaded all space. If this were the case then, according to Galilean relativity, it should be possible to add your own velocity to the velocity of incoming light so that if you were travelling at a half the speed of light then any light approaching you would be observed to be travelling at 1.5 times the speed of light in the aether. Similarly, any light approaching you from behind would strike you at 0.5 times the speed of light in the aether.

If one assumes both that the Maxwell equations are valid, and that Galilean relativity applies then there should be a preferred reference frame, the frame of the stationary aether. The preferred reference frame could be considered the true zero point to which all velocity measurements could be referred.

Special relativity restored a principle of relativity in physics by maintaining that Maxwell's equations are correct but that Galilean relativity is wrong: there is no preferred reference frame. Special relativity brought back the interpretation that in all inertial reference frames the same physics is going on and there is no phenomenon that would allow an observer to pinpoint a zero point of velocity. Einstein extended the principle of relativity by proposing that the laws of physics are the same regardless of the inertial frame of reference. According to Einstein, whether you are in the hold of Galileo's ship or in the cargo bay of a space ship going at a large fraction of the speed of light and the laws of physics will be the same.

[edit] Frames of reference, events and transformations

Before proceeding further with the analysis of relative motion the concepts of reference frames, events and transformations need to be defined more closely.

Physical observers are considered to be surrounded by a reference frame which is a set of coordinate axes in terms of which position or movement may be specified or with reference to which physical laws may be mathematically stated.

An event is something that happens independently of the reference frame that might be used to describe it. Turning on a light or the collision of two objects would constitute an event.

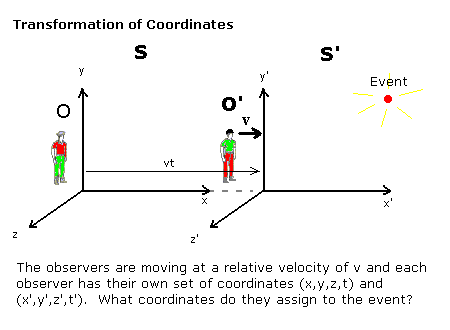
Suppose there is a small event, such as a light being turned on, that is at coordinates x,y,z,t in one reference frame. What coordinates would another observer, in another reference frame moving relative to the first at velocity v along the x axis assign to the event? This problem is illustrated below:

Relstandard.gif

What we are seeking is the relationship between the second observer's coordinates x',y',z',t' and the first observer's coordinates x,y,z,t. According to Galilean Relativity:

x' = x − vt

y' = y

z' = z

t' = t

This set of equations is known as a Galilean coordinate transformation or Galilean transformation.

These equations show how the position of an event in one reference frame is related to the position of an event in another reference frame. But what happens if the event is something that is moving? How do velocities transform from one frame to another?

The calculation of velocities depends on Newton's formula: v = dx / dt. The use of Newtonian physics to calculate velocities and other physical variables has led to Galilean Relativity being called Newtonian Relativity in the case where conclusions are drawn beyond simple changes in coordinates. The velocity transformations for the velocities in the three directions in space are, according to Galilean relativity:

\mathbf{u^'_x = u_x - v}

\mathbf{u^'_y = u_y}

\mathbf{u^'_z = u_z}

This result is known as the classical velocity addition theorem and summarises the transformation of velocities between two Galilean frames of reference. It means that the velocities of projectiles must be determined relative to the velocity of the source and destination of the projectile. For example, if a sailor throws a stone at 10 km/hr from Galileo's ship which is moving towards shore at 5 km/hr then the stone will be moving at 15 km/hr when it hits the shore.

In Newtonian Relativity the geometry of space is assumed to be Euclidean and the measurement of time is assumed to be the same for all observers.

The derivation of the classical velocity addition theorem is as follows:
If the Galilean transformations are differentiated with respect to time:
x' = x − vt
So:
dx' / dt = dx / dt − v
But in Galilean relativity t' = t and so dx' / dt' = dx' / dt therefore:
dx' / dt' = dx / dt − v
dy' / dt' = dy / dt
dz' / dt' = dz / dt
If we write u^'_x = dx^'/dt^' etc. then:
u^'_x = u_x - v
u^'_y = u_y 
u^'_z = u_z

[edit] The postulates of special relativity

1. First postulate: the principle of relativity

Observation of physical phenomena by more than one inertial observer must result in agreement between the observers as to the nature of reality. Or, the nature of the universe must not change for an observer if their inertial state changes. Every physical theory should look the same mathematically to every inertial observer. Formally: the laws of physics are the same regardless of inertial frame of reference.

2. Second postulate: the invariance of the speed of light

The speed of light in vacuum, commonly denoted c, is the same for all inertial observers, is the same in all directions, and does not depend on the velocity of the object emitting the light. Formally: the speed of light in free space is a constant in all inertial frames of reference.

Using these postulates Einstein was able to calculate how the observation of events depends upon the relative velocity of observers. He was then able to construct a theory of physics that led to predictions such as the equivalence of mass and energy and early quantum theory.

Einstein's formulation of the axioms of relativity is known as the electrodynamic approach to relativity. It has been superseded in most advanced textbooks by the space-time approach but it is equally valid and represents a tour de force of deductive reasoning which provided the insights required for the modern treatment of the subject.

[edit] Einstein's Relativity - the electrodynamic approach

Einstein asked how the lengths and times that are measured by the observers might need to vary if both observers found that the speed of light was constant. He looked at the formulae for the velocity of light that would be used by the two observers, (x = ct) and (x' = ct'), and asked what constants would need to be introduced to keep the measurement of the speed of light at the same value even though the x' axis was continually expanding. His working is shown in detail in the appendix. The result of this calculation is the Lorentz Transformation Equations:

x' = \gamma (x - vt)\,
y' = y \,
z' = z \,
t' = \gamma (t - \frac{v x}{c^{2}})\,

Where the constant \gamma = \frac {1}{\sqrt {1 -\frac{v^2}{c^2}}}.

The Lorentz Transformation is the equivalent of the Galilean Transformation with the added assumption that everyone measures the same velocity for the speed of light no matter how fast they are travelling. The speed of light is a ratio of distance to time (ie: metres per second) so for everyone to measure the same value for the speed of light the length of measuring rods, the length of space between light sources and receivers and the number of ticks of clocks must dynamically differ between the observers. So long as lengths and time intervals vary with the relative velocity of two observers (v) as described by the Lorentz Transformation the observers can both calculate the speed of light as the ratio of the distance travelled by a light ray divided by the time taken to travel this distance and get the same value.

Einstein's approach is "electrodynamic" because it assumes, on the basis of Maxwell's equations, that light travels at a constant velocity. As mentioned above, the idea of a universal constant velocity is strange because velocity is a ratio of distance to time. Do the Lorentz Transformation Equations hide a deeper truth about space and time? Einstein himself (Einstein 1920) gives one of the clearest descriptions of how the Lorentz Transformation equations are actually describing properties of space and time itself. His general reasoning is given below.

If the equations are combined they satisfy the relation:

(1) x^{'2} - c^2t^{'2} = x^2 - c^2t^2 \,

Einstein (1920) describes how this can be extended to describe movement in any direction in space:

(2) x^{'2} + y^{'2} + z^{'2} - c^2t^{'2} = x^2 + y^2 + z^2 - c^2t^2 \,

Equation (2) is a geometrical postulate about the relationship between lengths and times in the universe. It suggests that there is a constant s such that:

s^2 = x^{'2} + y^{'2} + z^{'2} - c^2t^{'2} \,
s^2 = x^2 + y^2 + z^2 - c^2t^2 \,

This equation was recognised by Minkowski as an extension of Pythagoras' Theorem (ie: s2 = x2 + y2), such extensions being well known in early twentieth century mathematics. What the Lorentz Transformation is telling us is that the universe is a four dimensional spacetime and as a result there is no need for any "aether". (See Einstein 1920, appendices, for Einstein's discussion of how the Lorentz Transformation suggests a four dimensional universe but be cautioned that "imaginary time" has now been replaced by the use of "metric tensors").

Einstein, A. (1920). Relativity. The Special and General Theory. Methuen & Co Ltd 1920. Written December, 1916. Robert W. Lawson (Authorised translation). http://www.bartleby.com/173/

[edit] Inertial reference frames

The Lorentz Transformation for time involves a component (vx / c2) which results in time measurements being different along the x-axis of relatively moving observers. This means that the old idea of a frame of reference that simply involves three space dimensions with a time that is in common between all of the observers no longer applies. To compare measurements between observers the concept of a "reference frame" must be extended to include the observer's clocks.

An inertial reference frame is a conceptual, three-dimensional latticework of measuring rods set at right angles to each other with clocks at every point that are synchronised with each other (see below for a full definition). An object that is part of, or attached to, an inertial frame of reference is defined as an object which does not disturb the synchronisation of the clocks and remains at a constant spatial position within the reference frame. The inertial frame of reference that has a moving, non-rotating body attached to it is known as the inertial rest frame for that body. An inertial reference frame that is a rest frame for a particular body moves with the body when observed by observers in relative motion.

Inertial.svg

This type of reference frame became known as an "inertial" frame of reference because, as will be seen later in this book, each system of objects that are co-moving according to Newton's law of inertia (without rotation, gravitational fields or forces acting) have a common rest frame, with clocks that differ in synchronisation and rods that differ in length, from those in other, relatively moving, rest frames.

There are many other definitions of an "inertial reference frame" but most of these, such as "an inertial reference frame is a reference frame in which Newton's First Law is valid" do not provide essential details about how the coordinates are arranged and/or represent deductions from more fundamental definitions.

The following definition by Blandford and Thorne(2004) is a fairly complete summary of what working physicists mean by an inertial frame of reference:

"An inertial reference frame is a (conceptual) three-dimensional latticework of measuring rods and clocks with the following properties: (i ) The latticework moves freely through spacetime (i.e., no forces act on it), and is attached to gyroscopes so it does not rotate with respect to distant, celestial objects. (ii ) The measuring rods form an orthogonal lattice and the length intervals marked on them are uniform when compared to, e.g., the wavelength of light emitted by some standard type of atom or molecule; and therefore the rods form an orthonormal, Cartesian coordinate system with the coordinate x measured along one axis, y along another, and z along the third. (iii ) The clocks are densely packed throughout the latticework so that, ideally, there is a separate clock at every lattice point. (iv ) The clocks tick uniformly when compared, e.g., to the period of the light emitted by some standard type of atom or molecule; i.e., they are ideal clocks. (v) The clocks are synchronized by the Einstein synchronization process: If a pulse of light, emitted by one of the clocks, bounces off a mirror attached to another and then returns, the time of bounce tb as measured by the clock that does the bouncing is the average of the times of emission and reception as measured by the emitting and receiving clock: tb = 1 / 2(te + tr).¹

¹For a deeper discussion of the nature of ideal clocks and ideal measuring rods see, e.g., pp. 23-29 and 395-399 of Misner, Thorne, and Wheeler (1973)."

Special Relativity demonstrates that the inertial rest frames of objects that are moving relative to each other do not overlay one another. Each observer sees the other, moving observer's, inertial frame of reference as distorted. This discovery is the essence of Special Relativity and means that the transformation of coordinates and other measurements between moving observers is complicated. It will be discussed in depth below.

Inertialoverlay.GIF

Blandford, R.D. and Thorne, K.S.(2004). Applications of Classical Physics. California Institute of Technology. See: http://www.pma.caltech.edu/Courses/ph136/yr2004/

Continue

Retrieved from "http://en.wikibooks.org/wiki/Special_Relativity/Principle_of_Relativity"