Special Relativity/Mathematical transformations
The teaching of Special Relativity on undergraduate physics courses involves a considerable mathematical background knowledge. Particularly important are the manipulation of vectors and matrices and an elementary knowledge of curvature. The background mathematics is given at the end of this section and can be referenced by those who are unfamiliar with these techniques.
The Lorentz transformation
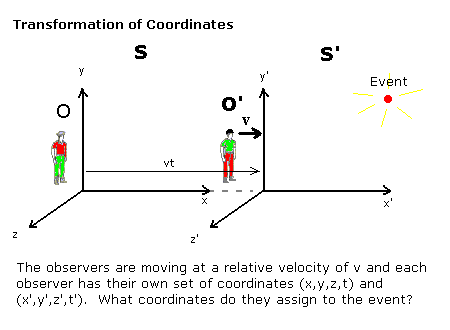
[edit | edit source]The Lorentz transformation deals with the problem of observers who are moving relative to each other. How are the coordinates of an event recorded by one observer related to the coordinates of the event recorded by the other observer? The standard configuration used in the calculation of the Lorentz transformation is shown below:
There are several ways of deriving the Lorentz transformations. The usual method is to work from Einstein's postulates (that the laws of physics are the same between all inertial reference frames and the speed of light is constant) whilst adding assumptions about isotropy, linearity and homogeneity. The second is to work from the assumption of a four dimensional Minkowskian metric.
In mathematics transformations are frequently symbolised with the "maps to" symbol:
The linearity and homogeneity of spacetime
[edit | edit source]Consider a clock moving freely. According to Newton's first law, objects continue in a state of uniform motion unless acted upon by a force; so, the velocity of the clock in any given direction () must be a constant.
If the clock is a real clock with readings given by then the rate of change with respect to these readings of the elapsed time at any other point in an inertial frame of reference, , will be a constant. If the clock were to tick at an uneven rate compared with other clocks then the universe would not be homogeneous in time—at some times the clock would appear to accelerate. This would also mean that Newton's first law would be broken and the universe would not be homogeneous in space.
If and are constant then is also constant. This means that the clock is not accelerating, i.e. that .
Linearity is demonstrated by the way that the length of things does not depend on position or relative position; for instance, if the distance between two points would depend upon the position of the observer whereas if the relationship is linear () separations are independent of position.
The linearity and homogeneity assumptions mean that the coordinates of objects in the inertial frame are related to those in the inertial frame by:
This formula is known as a Poincaré transformation. It can be expressed in indicial notation as:
If the origins of the frames coincide then can be assumed to be zero and the equation:
Those who are unfamiliar with the notation should note that the symbols etc. mean , , and so the equation above is shorthand for:
In matrix notation the set of equations can be written as:
The standard configuration (see diagram above) has several properties, for instance:
- The spatial origin of both observer's coordinate systems lies on the line of motion so the x axes can be chosen to be parallel.
- The point given by is the same as .
- The origins of both coordinate systems can coincide so that clocks can be synchronised when they are next to each other.
- The coordinate planes ,y, y' and z,z', can be arranged to be orthogonal (at right angles) to the direction of motion.
- Isotropy means that coordinate planes that are orthogonal at y=0 and z=0 in one frame are orthogonal at y'=0 and z'=0 in the other frame.
According to the relativity principle any transformations between the same two inertial frames of reference must be the same. This is known as the reciprocity theorem.
The Lorentz transformation
[edit | edit source]From the linearity assumption and given that at the origin so there is no constant offset then and , therefore K=1. So:
and, by the same reasoning:
Now, considering the x coordinate of the event, the z and y axes can be assumed to be 0 (ie: an arbitrary shift of the coordinates to allow the event to lie on the x axes). If this is done then the linearity consideration and the fact that and are the same point gives:
(1)
where is a constant. According to the reciprocity theorem we also have:
(2)
Einstein's assumption that the speed of light is a constant can now be introduced so that and also . So:
and
So:
and
Therefore the Lorentz transformation equations are:
The transformation for the time coordinate can derived from the transformation for the x coordinate assuming and or directly from equations (1) and (2) with a similar substitution for .
The coefficients of the Lorentz transformation can be represented in matrix format:
A coordinate transformation of this type, that is due to motion, is known as a boost.
The Lorentz transformation equations can be used to show that:
Although whether the assumptions of linearity, isotropy and homogeneity in the derivation of the Lorentz transformation actually assumed this identity from the outset is a moot point.
Given that: also equals and a continuous range of other transformations it is clear that:
The quantity is known as the spacetime interval and the quantity is known as the squared displacement.
A given squared displacement is constant for all observers, no matter how fast they are travelling, it is said to be invariant.
The equation:
is known as the metric of spacetime.
Another look at the Lorentz transformation
[edit | edit source]We have seen how length and duration both look different to a moving observer:
- lengths are contracted by a factor γ, when measured at the same time.
- durations are contracted by a factor γ, when measured in the same place.
We can extend these results to allow for measurements taking place at different times and places.
Lets consider two observers, O and O' such that O' is moving at velocity v along the x-axis with respect to O. We'll use primed variables for all the measurements O' makes.
We can assume for now both observers have the same origin and x-axis because we already know how to allow for observers being relatively rotated and displaced. We can put these complications back in later.
Now any length or duration can be written as the difference between two coordinates, for the two ends of the body or the start and end of the event, so it is sufficient to know how to change coordinates from one frame to the other.
We know how to do this in classical physics,
we need to extend this to relativity.
Notice that the in classical physics the relationship is linear; the graphs of these equations are straight lines. This makes the maths much simpler, so we will try to find a linear relationship between the coordinates for relativity, i.e equations of the general form
where m, n, p and q are all independent of the coordinates.
To begin with know that
- when t=0, x′ = γx (Lorentz contraction)
- when x=0, t′ = γt (Time dilation)
and that O' is travelling at velocity v. They measure their position to be at x′=0, but O measures it to be at vt so we must have
- x′=0 when x-vt=0
The only relationship between x and x′ that satisfies these criteria is
Both observers must measure the same speed for light,
or, substituting and rearranging,
The only linear relationship between t and t′ that satisfies these criteria is
So the primed and unprimed coordinates are related by
These equations are called the Lorentz transform.
They look simpler if we write them in terms of ct rather than t
Written this way they look much like the equations describing a rotation in three dimensions. In fact, once we allow for the different Pythagorean theorem, they are exactly like the equations for rotation.
- If observers are moving relative to each other, their coordinate systems are rotated in the (x,ct) plane.
The derivation of the constancy of the speed of light from the first postulate alone
[edit | edit source]The following text was taken from a "Wikiversity" lecture.
The lorentz transformation can be deduced from the first postulate alone with no additional assumptions.
The Lorentz transformation describes the way a vector in spacetime as seen by an observer O1 changes when it is seen by an observer O2 in a different inertial system.
The postulate of special relativity states that the laws of physics are independent of the velocity of an observer. This is equivalent to the requirement that the mathematical formulation of the laws of physics must be invariant if the coordinates of space and time are altered using a lorentz transformation.
This is the reason why the Lorentz transformation is a central concept in special relativity.
Four-vectors are vectors that, subjected to the Lorentz transformation, behave like vectors from spacetime. The standard approach to find relativistic laws to the corresponding non-relativistic ones is to find four-vectors to replace space vectors. Surprisingly often this simple approach is successful.
Here, for simplicity, the space coordinates are chosen so that the x-axis points in the direction in which O2 is moving with respect to O1 and the y and z coordinates are not considered.
Here is a way to determine a matrix that transforms coordinates from O1 to O2 where v is the velocity of O2 seen from O1.
Most generally, this matrix looks like and transforms to via .
The first requirement on this matrix is that O2 will be at rest (in space) within its own coordinate system.
Therefore for any time t.
This gives us and .
The backward transformation from O2 to O1 is described by the inverse matrix (where is the velocity of O1 seen from O2) has to leave O1 at rest in its own coordinates.
Assuming (being strict this would have to be proved) we have for any time resulting in .
The coefficients are functions of v. For all v the transformation is invertible, so .
For v=0 L(v) is the identity matrix, so b(0)=0. This allows to rewrite with a yet unknown function .
Now .
Now for every there exists a velocity such that
. Using what we have proved up to now gives
Comparing the diagonal components, we see immediately that for arbitrary values of , and so .
Using this we can rewrite the equation for the and by comparing each of the components at indeces (1,1) and (2,1) respectively. Substituting yields
from which we have .
Reinserting this into the first equation we have .
In case this simplifies to as is the identity matrix.
Let be an even function and an odd function
such that .
This gives us . Taking the logarithm and simplifying yields from which we get with any odd function . The negative sign is ruled out by .
Substituting in equation (1) verifies the solution but leaves us with
.
To prove we flip the direction of the x-axis in the base system as well as in the transformed system. The choice of the direction of the axis must not lead to different results. In the flipped coordinates the Lorentz transformation takes the form for .
On the other hand we can compute by using a coordinate transformation on :
from which we get and hence . Together with this gives .
Looking at the eigenvectors of L(v) we see they are independent of v.
This is equivalent to a transformation invariant velocity which experimentation shows to be equal to the speed of light. Altogether we have:
Note that for we would have the Galileian case with no finite invariant velocity.
Behold that if we did the same deduction not in the spacetime plane for (t, x) but in the space plane (x, y) with slope m=y/x instead of velocity v=x/t nothing would change except that, not by calculation but by experimentation alone, it would have turned out that and L(m) is just a rotation in the euclidian space with no real valued eigenvectors.
It is an interesting exercise to compare this result with the assumptions of reciprocity, homogeneity and isotropy mentioned earlier. Do the linear equations contained in the matrix formulation of the Lorentz transformation above assume a particular spacetime from the outset?
It is further important to mention that the determinant independent of velocity. This directly implicates that spacetime volumes are conserved.
The geometry of space-time
[edit | edit source]SR uses a 'flat' 4-dimensional Minkowski space, which is an example of a space-time. This space, however, is very similar to the standard 3 dimensional Euclidean space, and fortunately by that fact, very easy to work with.
The differential of distance(ds) in Cartesian 3D space is defined as:
where are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension, time, is added, with units of c, so that the equation for the differential of distance becomes:
In many situations it may be convenient to treat time as imaginary (e.g. it may simplify equations), in which case in the above equation is replaced by , and the metric becomes
Note that ds in this case is the distance, and not the interval. Caution should be exercised in the use of 'imaginary' time, it is not part of the modern theory of relativity. Blandford and Thorne (2004) in their "Applications of Classical Physics" (http://www.pma.caltech.edu/Courses/ph136/yr2004/ ), write the following about imaginary time: "(i) it hides the true physical geometry of Minkowski spacetime, (ii) it cannot be extended in any reasonable manner to non-orthonormal bases in flat spacetime, and (iii) it cannot be extended in any reasonable manner to the curvilinear coordinates that one must use in general relativity."
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3-D space
We see that things such as light which move at the speed of light lie along a dual-cone:
defined by the equation
or
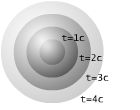
Which is the equation of a circle with . The path of something that moves at the speed of light is known as a null geodesic. If we extend the equation above to three spatial dimensions, the null geodesics are continuous concentric spheres, with radius = distance = c×(±time).
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old.", we are looking down this line of sight: a null geodesic. We are looking at an event meters away and d/c seconds in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the -t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
Length contraction, time dilation and phase
[edit | edit source]Consider two inertial frames in standard configuration. There is a rigid rod moving along in the second frame at v m/s. The length of the rod is determined by observing the positions of the end points of the rod simultaneously - if the rod is moving it would be nonsense to use any other measure of length. An observer who is moving at the same velocity as the rod measures its "rest length". The Lorentz transformation for coordinates along the x axis is:
Suppose the positions, , of the two ends of the rod are determined simultaneously (ie: is constant):
Or, using for the rest length of the rod and for the length of the rod that is measured by the observer who sees it fly past at v m/s:
Or, elaborating :
In other words the length of an object moving with velocity is contracted in the direction of motion by a factor in the direction of motion.
The Lorentz transformation also affects the rate at which clocks appear to change their readings. The Lorentz transformation for time is:
This transformation has two components:
and is a straight line graph (ie: ).
The gradient of the graph is so:
or:
Therefore clocks in the moving frame will appear to go slow, if is a time interval in the rest frame and is a time interval in the moving frame:
Or, expanding:
The intercept of the graph is:
This means that if a clock at point is compared with a clock that was synchronised between frames at the origin it will show a constant time difference of seconds. This quantity is known as the relativistic phase difference or "phase".
The relativistic phase is as important as the length contraction and time dilation results. It is the amount by which clocks that are synchronised at the origin go out of synchronisation with distance along the direction of travel. Phase affects all clocks except those at the point where clocks are syncronised and the infinitessimal y and z planes that cut this point. All clocks everywhere else will be out of synchronisation between the frames. The effect of phase is shown in the illustration below:
If the inertial frames are each composed of arrays of clocks spread over space then the clocks will be out of synchronisation as shown in the illustration above.
It is interesting to see how the phase term cancels out when time differences are being considered. It cancels out because the phase term is applied to the clock that is at a constant position in the primed frame. The Lorentz transform for time is:
A difference between two times is:
The important thing to note is that the clock is at the same position in its own reference frame.
The result is that:
Where the phase terms have cancelled.
Hyperbolic geometry
[edit | edit source]In the flat spacetime of Special Relativity:
Considering the x-axis alone:
The standard equation of a hyperbola is:
In the case of spacetime:
Spacetime intervals separate one place or event in spacetime from another. So, for a given motion from one place to another or a given fixed length in one reference frame, given time interval etc. the metric of spacetime describes a hyperbolic space. This hyperbolic space encompasses the coordinates of all the observations made of the given interval by any observers.
It is possible to conceive of rotations in hyperbolic space in a similar way to rotations in Euclidean space. The idea of a rotation in hyperbolic space is summarised in the illustration below:
A rotation in hyperbolic space is equivalent to changing from one frame of reference to another whilst observing the same spacetime interval. It is moving from coordinates that give:
to coordinates that give:
The formula for a rotation in hyperbolic space provides an alternative form of the Lorentz transformation ie:
From which:
The value of can be determined by considering the coordinates assigned to a moving light that moves along the x axis from the origin at flashes on for seconds then flashes off.
The coordinates assigned by an observer on the light are: , the coordinates assigned by the stationary observer are . The hyperbola representing these observations is illustrated below:
The equation of the hyperbola is:
but x=vt for the end of the flash so:
Now, from hyperbolic trigonometry:
But so:
and, from the hyperbolic trigonometric formula :
Inserting these values into the equations for the hyperbolic rotation:
Which gives the standard transform for x:
In a similar way is equivalent to:
So the Lorentz transformations can also be derived from the assumption that boosts are equivalent to rotations in hyperbolic space with a metric .
The hyperbolic angle is known as the rapidity of the boost.
Addition of velocities
[edit | edit source]Suppose there are three observers 1, 2, and 3 who are moving at different velocities along the x-axis. Observers 1 and 2 are moving at a relative velocity and observers 2 and 3 are moving at a relative velocity of . The problem is to determine the velocity of observer 3 as observed by observer 1 ().
It turns out that there is a very convenient relationship between rapidities that solves this problem:
If and then:
In other words the rapidities can be simply added from one observer to another ie:
Hence:
So the velocities can be added by simply adding the rapidities. Using hyperbolic trigonometry:
Therefore:
Which is the relativistic velocity addition theorem.
The relationship is shown below:
Velocity transformations can be obtained without referring to the rapidity. The general case of the transformation of velocities in any direction is derived as follows:
where etc. are the components of the velocity in the x, y, z directions.
Writing out the components of velocity:
But from the Lorentz transformations:
Therefore:
Dividing top and bottom of each fraction by :
Substituting
The full velocity transformations are tabulated below:
|
|
|
|
|
|
|
|
|
Having calculated the components of the velocity vector it is now possible to calculate the magnitudes of the overall vectors between frames:
Addition of velocities - another approach
[edit | edit source]In classical physics, velocities simply add. If an object moves with speed u in one reference frame, which is itself moving at v with respect to a second frame, the object moves at speed u+v in that second frame.
This is inconsistent with relativity because it predicts that if the speed of light is c in the first frame it will be v+c in the second.
We need to find an alternative formula for combining velocities. We can do this with the Lorentz transform.
Because the factor v/c will keep recurring we shall call that ratio β.
We are considering three frames; frame O, frame O' which moves at speed u with respect to frame O, and frame O" which moves at speed v with respect to frame O'.
We want to know the speed of O" with respect to frame O,U which would classically be u+v.
The transforms from O to O' and O' to O" can be written as matrix equations,
where we are defining the β's and γ's as
We can combine these to get the relationship between the O and O" coordinates simply by multiplying the matrices, giving
This should be the same as the Lorentz transform between the two frames,
These two sets of equations do look similar. We can make them look more similar still by taking a factor of 1+ββ' out of the matrix in (1) giving:
This will be identical with equation 2 if
Since the two equations must give identical results, we know these conditions must be true.
Writing the β's in terms of the velocities equation 3a becomes
which tells us U in terms of u and v.
A little algebra shows that this implies equation 3b is also true
Multiplying by c we can finally write.
Notice that if u or v is much smaller than c the denominator is approximately 1, and the velocities approximately add but if either u or v is c then so is U, just as we expected.
Acceleration transformation
[edit | edit source]This section is under development.
It was seen above that:
and, if and the velocity addition theorem can be expressed as the sum of the rapidities:
If we differentiate this equation with respect to to investigate acceleration, then assuming is constant:
so
(1)
But is also equal to:
But and the derivative of an arctangent is given by:
and hence:
For brevity we will use the notation:
ie: is gamma for observers moving at a relative velocity of .
So:
(2)
The velocity of the object observed by the unprimed and primed observers is:
and:
So:
and using the Minkowski metric:
So:
Hence:
Given that and
(3)
Therefore, substituting (2) and (3) in (1):
Applying the differential of arctanh as before to determine :
This is a different result from the Newtonian formula in which . The proper acceleration, is defined as the acceleration of an object in its rest frame. It is the instantaneous change in velocity for an observer for whom and . In these circumstances:
The term is called "coordinate acceleration".
Another approach to acceleration
[edit | edit source]Classically we would talk about a particle at x(t) with acceleration d²x/dt². In relativity we must treat time as just another coordinate, and use derivatives with respect to proper time, which means our notion of acceleration will change. We can assume the particle is moving slower than light.
Since τ increases monotonically with t (no time travel allowed) we can easily parameterise the path of the particle with τ rather than t. Derivatives with respect to these two variables then differ only by a factor of γ
which gives us the connection between the classical and relativistic formulae.
Lets suppose we have a particle moving on the path (x(τ),ct(τ)), where τ is the particle's proper time.
Its velocity four vector is
In the particles rest frame this is (0,c), which has constant magnitude -c2, but this scalar must be the same in all frames, thus
That is, the magnitude of the velocity is always constant.
Differentiating this, we can immediately say
so, velocity and acceleration are always perpendicular.
These two results are much simpler than in classical physics.
Differentiating the velocity gives us, after some algebra ,
when the motion is along the x-axis. Since the spatial and temporal components must be 3-vectors and scalars respectively we immediately see that for motion in arbitrary directions,
The magnitude of this is
which is the classical magnitude, corrected by a factor dependent on γ. When the velocity is much less than c this factor is approximately 1, so in that limit the magnitudes are the same, as they should be.
Knowing this, we can work out the equation of motion for a particle with constant acceleration a along the x-axis. For simplicity, we'll assume the initial velocity is 0.
Since the acceleration is constant
Integrating once we get
or, on rearranging
If at is much less than c this gives a velocity of approximately at, identical to the classical result, but as t tends to infinity the velocity tends to c.
The position is
where d is some constant. We can choose our coordinate system to make d zero.
Calling the interval between the origin and the particle, I, we have
Thus the interval between the particle and the origin is constant. Notice, this is the equation for an hyperbola, so we know the particle's trajectory.
Momentum
[edit | edit source]Classically, momentum is velocity multiplied by mass. We can use the same definition in relativity, and see where it takes us.
You may sometimes see the product m0γ which shows up here called the relativistic mass, but we will not be using this approach.
The mass, m0, is generally called the rest mass, to distinguish it from the relativistic mass.
The spatial component of the four-momemntum is clearly the classical momentum, scaled by a factor of γ. At speeds much less than c this will be approximately 1.
The temporal component is m0γc. To see what this means we can look at its value when v/c is small.
The first term in this expansion is a constant.
The second term is
which we recognise as being the classical kinetic energy, divided by c.
Now, adding a constant to the definition of kinetic energy makes no real difference, since all that matters are changes in energy, so we can identify this temporal component of relativistic momentum with the energy over c.
We then have
Even at rest, the particle has a kinetic energy,
the most famous relativistic equation.
Force
[edit | edit source]Classically, we have
We can get the equivalent relativistic equation simply by replacing 3-vectors with 4-vectors and t with τ, giving
Provided the rest mass is constant, as it is for all simple systems, we can rewrite this as
We already know about a so we can now write
The temporal component of this is essentially the power, the rate of change of energy with time, as might be expected from energy being the temporal component of momentum.
Accelerated Frames and Event Horizons
[edit | edit source]Figure: Spacetime diagram showing the world line of the origin of a reference frame undergoing constant acceleration.
We know this world line is an hyperbola, with asymptotes x=±ct. Looking at the diagram show another property.
No light from the 'twilight zone', where x is smaller than ct, can ever reach the accelerated observer. Hence, no event in the twilight zone can affect the observer.
Conversely, there is a region, where x is smaller than -ct, which no light from the accelerated observer can ever reach. Hence the observer can not affect any events in this region.
Because of this we call the two asymptotes event horizons. In some ways, they are like one-way barriers in space-time. The accelerated observer can see objects vanishing behind an event horizon, but they never see any re-emerge from it.
These particular event horizons are observer dependent, as are all event horizons in special relativity. However, general relativity permits event-horizons which are observer independent.
We are not going to prove this, but we can some idea about how event horizons apply to general relativity by using its basic principle, called the equivalence principle by Einstein: that gravity is nothing more than an inertial force.
This means that gravity is locally indistinguishable from forces due to acceleration; if the elevator doors are closed, we can't tell whether we are stationary in a 1g gravity field or being accelerated at 1g in zero gravity.
This suggests that something can be learned about general relativity by examining the properties of accelerated reference frames
Now, since the gravitational force on the Earth points downward, it follows that we must be constantly accelerating upward as we stand on the surface of the Earth. The obvious problem with this interpretation of gravity is that we don't appear to be moving away from the center of the Earth, which would seem to be a natural consequence of such an acceleration.
However, the calculation of the previous chapter shows that even though the object associated with the curved world line in the figure above is accelerating away from the origin, it always remains the same distance (in its own frame) from the origin. In other words, even though we are accelerating away from the center of the Earth, the distance to the center of the Earth remains constant!
Therefore, because of the equivalence principle, we can expect to see the same things as an accelerated observer in special relativity, including an event horizon.
For acceleration in special relativity, inertial objects pass the event horizon at speed c at time infinity, relative to the observer.
Similarly, in general relativity, freely falling objects pass the event horizon at speed c at time infinity, relative to a static observer. By reversing the trajectories we can conclude that at the event horizon the escape velocity is c, i.e gravity is so strong light can not escape.
Thus, using the equivalence principle, and behaviour under acceleration in special relativity, we've predicted black holes.
There isn't actually an event horizon inside the earth, since the mass of the earth is not concentrated in a point and the earth can only be treated as a point mass while outside the earth's surface, which lies outside where the event horizon should otherwise have been.
The red shift
[edit | edit source]Spacetime diagram for explaining the gravitational red shift.
Light emitted at a lower level in a gravitational field has its frequency reduced as it travels to a higher level. This phenomenon is called the gravitational red shift.
We can see why this happens by using the principle of equivalence. Being in a gravitational field is equivalent to being in an accelerated frame, so knowing how the doppler shift works in such a frame will tell us how it works in a gravitational field.
We view the process of light emission and absorption from the unaccelerated or inertial frame, as shown in the figure above. In this reference frame the observer of the light is accelerating to the right, as indicated by the curved red world line, which is equivalent to a gravitational force to the left.
The light is emitted at point A with frequency by a source which is stationary at this instant. At this instant the observer is also stationary in this frame. However, by the time the light gets to the observer, they have a velocity to the right which means that the observer measures a Doppler shifted frequency for the light. Since the observer is moving away from the source, , as indicated above.
The relativistic Doppler shift is given by
so we need to compute U/c. The line of simultaneity for the observer at point B goes through the origin, and is thus given by line segment OB. The slope of this line is U/c, where U is the velocity of the observer at point B. From the figure we see that this slope is also given by the ratio X' /X.
Equating these, eliminating X in favor of L = √(X2 - X′2), which is the actual invariant distance of the observer from the origin, and substituting into the previous equation results in our gravitational red shift formula:
If X′ = 0, then there is no redshift, because the source is collocated with the observer. On the other hand, if the source is located at the origin, so X′=X, the Doppler shifted frequency is zero. In addition, the light never gets to the observer, since the world line is asymptotic to the light world line passing through the origin. If the source is at a higher level in the gravitational field than the observer, so that X′ < 0, then the frequency is shifted to a higher value, i. e., it becomes a blue shift.
To see how this doppler shift relates to the strength of gravity, g, and the distance h between the source and the observer, first note that
Making these substitutions gives
So the redshift is proportional to gravity.
Since this doppler shift doesn't depend on the type of wave we can conclude that it is actually caused by time dilation, just like the doppler shift due to relative motion.
That is, gravity slows down time.
Energy and frequency
[edit | edit source]In equation 1 gh is the change in gravitational potential energy so the change in frequency is proportional to change in potential energy, which suggests there might be a connection with energy conservation.
However, since we haven't yet established any connection between frequency and energy, we can't simply apply an energy conservation argument. Instead, we can argue in reverse, finding out what the energy-frequency relationship must be if energy is to be conserved.
Suppose we have two identical systems, both at rest in a uniform gravitational field g with initial energy E separated by a vertical distance h.
The system has mass E/c2, giving it potential energy, so the total energy of the two systems is initially
where the second term is due to the lesser potential energy of the lower system.
The lower system emits a burst of waves, frequency ω, energy E(ω). When this reaches the upper system the waves have been red-shifted to frequency ω', energy E(ω'). This energy is absorbed by the upper system.
The total energy is now
Since we want to preserve energy conservation, these two equations must give the same result. Equating them, we get
Comparing this with the doppler shift we see that
which can only be true if E(ω) is proportional to ω
I.e, energy conservation implies energy is proportional to frequency, which is one of the axioms of quantum theory.
We could equally well have started with the quantum result and proved the gravitational red shift must exist. Either theory requires the other for consistency.
Since energy and frequency are each the temporal components of a four-vector, their being proportional implies the four-vectors themselves, and their spatial components, are also proportional. So, for waves, momentum is proportional to k.
Remember too, we saw earlier, when we looked at Hamilton's equations, that classical mechanics would be equivalent to a theory of anisotropic waves, in the geometrical optics limit, if energy were proportional to frequency and momentum to wave number. This proportionality isn't just required for energy conservation, it would make possible a theory uniting waves and particles.
None of this actually proves the proportionality, doing that requires experiment, but it does make it a natural assumptiom, which is indeed confirmed by experiment.
Because of all this, from now on we'll assume that energy and frequency are related in this way, with the constant of proportionality being
Gravity and curvature
[edit | edit source]The gravitational redshift also implies that space is curved. We can see this by considering a rectangle in space-time.
Without gravity, if we start at some point A, wait for time t, then move at light-speed to the right for a distance h, we get to the same place, B, as if we move at light-speed for a distance h then wait for time t at rest with respect to A.
With gravity, if we follow the first path, we rise a distance of ct then wait for time t. On the second path, we begin by waiting for time t, but this is dilated by gravity. To an observer at B we appear to be waiting for a time t(1+gh/c2) before we start, so we end up at B later than on the first path.
Thus, with gravity, it matters which order we add distance vectors in. This can't happen if space is flat, so space must be curved.
To describe how it's curved we'd need the techniques of General Relativity.
External Links
[edit | edit source]Potential Momentum
[edit | edit source]In classical physics we know that kinematics can often be described by a potential energy alone. Now we've seen that in relativity the energy is just the temporal component of the momentum 4-vector, so we should expect the same of the potential energy. To see how this works, we'll reason by analogy from the classical case.
For a free, non-relativistic particle of mass m, the total energy E equals the kinetic energy K and is related to the momentum Π of the particle by
In the non-relativistic case, the momentum is Π= mv, where v is the particle velocity.
If the particle is not free, but is subject to forces associated with a potential energy U(x,y,z), then the equation must be modified to account for the contribution of U to the total energy:
The force on the particle is related to the potential energy by
For a free, relativistic particle, we have
The obvious way to add forces to the relativistic case is by rewriting this equation with a potential energy:
However is a four-vector, so an equation with something subtracted from just one of the components of this four-vector is not relativistically invariant. In other words, this equation doesn't obey the principle of relativity, and therefore cannot be correct!
How can we fix this problem? One way is to define a new four-vector with U/c being its timelike part and some new vector Q being its spacelike part:
We then subtract Q from the momentum Π. When we do this, equation (13.5) becomes
The quantity Q is called the potential momentum and Q is the potential four-momentum.
If |Π-Q| is much smaller than mc, this becomes approximately
This expression for the energy has the same form as the Hamiltonian we looked at for classical velocity dependent forces, so we know it predicts a force perpendicular to the velocity, when the condition is met. It turns out to be perpendicular even when the condition is met.
In classical physics the potential momentum is an optional extra. In relativity it is a necessary part of any potential field.
Some additional terminology is useful. We define
as the kinetic momentum since in the classical case it reduces to mv. In order to avoid confusion, we rename Π the total momentum. Thus, the total momentum equals the kinetic plus the potential momentum, in analogy with energy.
Conservation of 4 momentum
[edit | edit source]We earlier introduced the ideas of energy and momentum conservation. In other words, if we have a number of particles isolated from the rest of the universe, each with momentum pi and energy Ei, then particles may be created and destroyed and they may collide with each other.
In these interactions the energy and momentum of each particle may change, but the sum total of all the energy and the sum total of all the momentum remains constant with time:
The expression is simpler in terms of four-momentum:
At this point a statement such as the one above should ring alarm bells. Just what does it mean to say that the total energy and momentum remain constant with time in the context of relativity? Which time? The time in which reference frame?
Suppose two particles exchange four-momentum remotely at the time indicated by the fat horizontal bar in the left panel. Conservation of four-momentum implies that
where the subscripted letters correspond to the particle labels in the figure. Primed values refer to the momentum after the exchange while no primes indicates values before the exchange.
Now view the exchange from the reference frame in the right panel. A problem with four-momentum conservation exists in the region between the thin horizontal lines. In this region particle B has already transferred its four-momentum, but it has yet to be received by particle A. In other words, four-momentum is not conserved in this reference frame!
This problem is so serious that we must eliminate the concept of action at a distance from the repertoire of physics. The only way to have particles interact remotely and still conserve four-momentum in all reference frames is to assume that all remote interactions are mediated by another particle, or by a field.
If the force is being mediated by a particle then first, particle A emits particle C in a manner which conserves the four-momentum. Second, particle C is absorbed by particle B in a similarly conservative interaction.
If the force is being mediated by a field then first, particle A emits wave C, with momentum proportional to its wavenumber in a manner, which conserves the four-momentum. Wave C then travels at c or less until it is absorbed by particle B in a similarly conservative interaction.
We'll see that in quantum theory the difference between a particle and a field vanishes, so these two pictures actually both describe the same mechanism a different perspective. Which every picture we use, four-momentum is conserved at all times in all reference frames.
In other words, momentum and energy are transferred from particle A to particle B in a two step process. In between the momentum resides in a particle or field.