Chapter 2 - Orbital Mechanics
1.0 - Introduction
[edit | edit source]
Objects in the Universe are in rapid motion relative to each other, and to the Universe as a whole, mostly under the influence of gravity. This is in contrast to the solid surface of the Earth, whose parts are stationary to each other, or moving very slowly. Celestial Mechanics is the subject that deals with the motions of natural objects in space, while Astrodynamics or Orbital Mechanics is the application of the same principles to artificial objects, with the addition of artificial forces like thrust and lift.
The motions of the planets, Moon, and Sun have been studied since ancient times, and on a scientific basis starting about 500 years ago. With the advent of artificial spacecraft, the subject has shifted from just observing natural bodies, to planning and executing missions to and around them. The relevance of this subject to space systems is, of course, that travel to a desired destination or orbit requires using celestial and orbital mechanics to calculate where that destination will be, and how to get there.
Space travel is a complex subject when high accuracy is needed. Minor effects like the gravity of non-spherical objects and light pressure then have to be accounted for. This chapter only covers some of the basic ideas and simple examples. More detailed and advanced information can be found in
- the Wikibook Astrodynamics, and Wikipedia articles in the Category Astrodyamics, and the series on astrodynamics noted in the Orbital Mechanics article.
- Textbooks such as Orbital Mechanics and Astrodynamics, Hintz, 2015, Fundamentals of Astrodynamics 2nd, Bate, 2020, and Fundamentals of Astrodynamics and Applications 4th, Vallado, 2013
- The 2008 MIT Open Course Astrodynamics.
2.0 - Orbits
[edit | edit source]
Gravity has no limiting distance - every object in the Universe is affected by the gravity of every other object. For practical purposes, the force of gravity from most of the Universe cancels out, since there is about the same amount of material in all directions. What remains are more massive and nearby objects, whose gravity is large enough to matter for a given calculation. Which objects matter depends on how accurate your results need to be. Preliminary calculations around a single large body can be done with formulas like the ones below. Multiple objects in general follow orbits, and move in relation to each other. So the strength and direction of their gravity varies. So detailed calculations use computer simulations that account for these changes across time.
An Orbit is the path that an object will follow when only affected by gravity. Orbits around uniform single bodies are Conic Sections, the shapes generated by slicing a cone. Orbital Eccentricity describes the shape as a number, where 0 is a circle, between 0 and 1 is an ellipse, 1 is a parabola, and more than 1 is a hyperbola.
Circular and elliptical orbits are bound to the body being orbited and will repeat. Parabolic and hyperbolic orbits are not bound to the body, and do not repeat, but are influenced by its gravity. Simple orbit calculations only consider the nearest massive body. This is suitable when that body's attraction is much greater than other bodies, and for short time periods. More detailed and accurate calculations have to consider non-uniformity of the main body, and other bodies with enough gravity to influence the accuracy of the result.
An ideal case is a single uniform spherical massive object. A circular orbit around it will have a constant speed and distance around the center of mass of the body. This also means it has a constant Orbital Period, the time to complete one revolution around the body and return to the starting point. The circular orbit velocity, vo, around any body can be found from
where G is the Gravitational constant (6.67 x 10-11 Nm2/s2) that relates mass to force of gravity, M is the mass of the body in kg, and r is the radius to the center of the body in meters. Since G is a universal constant, and a body's mass is nearly constant, the Standard Gravitational Parameter μ = GM can be used. For Earth, if we neglect falling meteors, atmosphere leakage, and things we launch away from it, this is 3.986 x 1014 m3/s2.
The orbital period, P, in seconds of a small body orbiting a large one in a circular or elliptic orbit with semi-major axis a (Figure 1-1) is
Escape velocity, ve the amount needed to reach an infinite distance from an object, is found by
Since this formula is the same as that for circular orbit, except by a factor of 2 in the square root term, escape velocity is the square root of 2 (1.414+) times circular orbit velocity. Elliptical orbits will have a velocity at the nearest point to the body, or Periapsis, in between that of circular and escape.
2.1 - Orbital Elements
[edit | edit source]
Orbital Elements are the parameters required to fully describe the location and orientation of an orbit, the shape of the orbit, and the position of an orbiting object at a given time. They are described relative to the major body the smaller one orbits. These elements change over time under the gravitational influence of other objects. They also change from non-ideal shape and mass distribution of the major body, the effects of relativity, and outside forces like drag and light pressure. The more important elements include:
Axes - Periodic orbits are generally ellipses. An ellipse has a major and minor axis, which are the longest and shortest distances across the center of the ellipse. These axes are perpendicular to each other (Figure 1-1). Half of these axes, or the distances from center to edge of the ellipse, are called the Semi-major and Semi-minor axes respectively, with symbols a and b. The semi-major axis is the value usually used to describe the overall size of an orbit.
Eccentricity - The foci of an ellipse are the two points along the major axis such that the sum of the distances from the foci to any point on the ellipse is constant. An orbit of a small body around a more massive one will have the massive one located at one focus of the elliptical orbit. The Focal length, f, is the distance from a focus to the center of the ellipse. The shape of the orbit is measured by Eccentricity, e, which is defined as:
Periapsis and Apoapsis - The higher the eccentricity, the smaller the ratio of the minor to major axis lengths, and the greater the difference between the nearest and farthest points of the orbiting body from the one it is orbiting. The prefixes peri- and ap- refer to these nearest and farthest points of an orbit. Different suffixes are used to indicate what body is being orbited, such as perigee and apogee for the lowest and highest points of an Earth orbit, and perihelion and aphelion for distance from the Sun. The general symbols q and Q are used for the minimum and maximum distances. These are measured from the center of the larger body. Orbit altitude is the distance to the surface in the direction of the center, and is always smaller. The minimum and maximum distances can by found by the formulas
2.2 - Lagrangian Points
[edit | edit source]

Given two large bodies, such as the Sun and Jupiter, with the second orbiting the first, and a third small body, such as an asteroid, there are five points relative to the large bodies where the net forces keep the small body in approximately the same position relative to the two larger ones. These are called Lagrange Points (Figure 2-1) after one of the mathematicians who discovered them.
Three of these, labeled L1, L2, and L3, are unstable. If you move slightly away from the exact point, you will tend to move further away. The other two, L4 and L5, are stable. Slight movements around these points will not cause the small body to drift away, but rather orbit around the points. L1, L2, and L3 are located between, behind, and opposite the second of the large bodies, respectively. L4 and L5 are located in the same orbit as the second large body, 60 degrees ahead and behind it.
As the largest planet, Jupiter has the largest collection of asteroids in it's Lagrange points. These asteroids are called the Jupiter Trojans, since the first few at Jupiter were named after characters in the Trojan War in Homer's Illiad. 12,600 such asteroids were known by mid-2023. More generally, objects at the Lagrange points of other planets are also called X Trojans, where X is the planet they are related to.
Since most planet orbits are elliptical, the Lagrange points shift as the distance between the two major bodies changes. The asteroids are therefore not all at the exact points, but rather distributed in the stable regions near them, and move around the points. Lagrange points can also exist around a planet with a large moon such as the Earth's. If the moon is too far from the planet, the Sun's influence can disrupt the stable points, as can having multiple large moons.
Lagrange points are useful for space projects, because they have a fixed location relative to the associated planet or moon, and are either stable, or need very little propulsion to maintain position. A number of Spacecraft are or plan to use these locations, in addition to natural objects found there.
2.3 - Rotation
[edit | edit source]
Nearly every natural body rotates, so that the direction from the body's center to a fixed surface point changes with respect to the Universe as a whole. As a practical matter bright stars are used as the reference for rotation. These are called the Fixed Stars because they were originally thought to be attached to a celestial sphere around the Earth. In reality, stars are independent objects at different distances and move relative to each other. It took modern instruments to measure their distances and movements. The rotation of most objects is fast relative to the average motion of stars, so the stars can be treated as a stationary reference frame.
Several properties of a body can be measured relative to this reference frame, or relative to a larger body it orbits:
Rotation Period - is the time it takes the body to complete one rotation with respect to the stars, the Sun, or a planet if it orbits one. The most obvious effect of the rotation period is the day-night cycle on Earth. Some objects become Tidally Locked into a rotational resonance with the parent body they orbit. This means the rotation period is a simple ratio to the orbit period. The Moon is the most obvious example of this, with a 1:1 ratio. The result is one side always faces the Earth, with a small wobble. The planet Mercury is in a 3:2 resonance, meaning it rotates three times for every two orbits around the Sun.
Rotation defines an axis around which the object rotates (Figure 2-2). The places where the axis meets the surface of the body are called poles, and the midpoint of the surface between the poles is called the Equator. On smaller bodies with irregular shape, the Equator may not be well defined. On larger bodies which are more or less round, the Equator has the largest distances from the rotation axis.
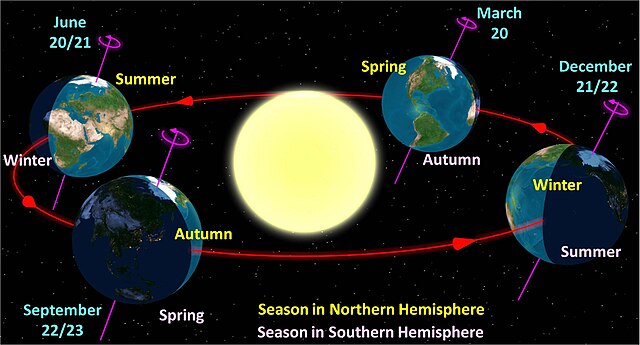
Axial Tilt - is the angle the body axis makes with the axis of the body's orbit. The latter is perpendicular to the orbit plane defined by the orbit's path. The rotational inertia of large bodies causes their rotation axis to remain relatively fixed relative to the stars. For example, the Earth's north pole points near the star Polaris, but this point is tilted 23.44 degrees from the axis of its orbit around the Sun. Over one orbit (1 year) first one pole then the other points somewhat towards the Sun, causing seasonal changes.
Rotational Velocity - On the surface of a rotating body, the circular motion about the axis produces an acceleration which opposes gravity. The velocity and acceleration depend on the distance from the axis and the rotation period. For example, at the Earth's equator the rotation velocity is 465 m/s, which generates an acceleration of 0.0338 m/s2, or about 3% of gravity. So apparent weight is less at the equator than the poles.
Depending on composition, objects more than 400-1000 km in diameter have internal forces greater than the strength of the internal materials. Their self-gravity forces them into a mostly rounded shape, a condition called Hydrostatic Equilibrium. The strength of solid materials allows some deviations such as mountains and basins. Liquid layers will flow freely according to gravity and rotation. Since rotation lowers gravity in some parts relative to others, larger bodies will assume a flattened or elongated shape. Smaller objects are only partly or not at all forced into roundness and can be very irregular.
The rotation of any body lowers the difference between orbit velocity and surface velocity when they are in the same direction. In the case of Earth it is 5.9% less, making it easier to reach orbit from low latitudes going east. In the case of asteroid 4 Vesta, surface rotation is as high as 93.5 m/s, or 36.7% of orbit velocity, a significant reduction. Very small objects which do not have structural flaws can even rotate faster than orbital velocity around them, producing areas where you cannot remain on the surface without mechanical aid.
2.4 - Tides and Perturbations
[edit | edit source]
Gravity forces extend to infinity. So nearby large objects, such as the Moon and Sun for the Earth, also add acceleration components to the gravity of the Earth. This varies over time as their direction and distance changes. The side of the Earth facing the Moon, for example, is pulled by it's gravity 6.6% more strongly than the opposite side, because it is closer in distance.
The difference in gravity between the near and far sides is called the Tidal Force because it is the source of ocean tides on Earth. Those tides happen because water is free to move under the weaker or stronger pull of the Moon relative to the Earth's center. The solid crust is more restricted by its strength. Tides do distort it but less than the oceans. Tidal forces affect other moons and planets too.
The Moon's orbit is tilted relative to the Earth's equator, as is the Earth relative to the Sun. So the combined tidal forces are not directly upwards from the Earth's surface, but at an angle. This causes the Earth's rotation axis to change direction relative to the stars, tracing a circle in 25,771 years. This is known as Axial Precession.
The lesser gravity of other bodies also affects the orbit of an object around the primary it is bound to in complex ways. For example, the Earth's orbit is primarily determined by the Sun, but the gravity of the other planets causes changes to it. These are called Perturbations. There are no simple formulas to describe the changes among three or more bodies. Instead complex mathematics or computer calculations are used.
On long time scales perturbations can drastically affect an orbit. This is most obvious in the case of Jupiter and comets. Long-Period Comets are often near escape velocity, so small velocity changes caused by the large mass of Jupiter can drastically change their orbits. This can lead to them becoming short period comets that stay near the Sun, or being ejected entirely from the Solar System.
3.0 - Velocity Map
[edit | edit source]
In contrast to Earth, where movement involves friction that must be overcome, space is a nearly frictionless environment. So distance does not matter as much as velocity changes, or Δv, which require energy or propellant to produce. The Greek letter delta in mathematics means change in a value, so velocity changes are often written out as "delta-V" in space systems work.
Figure 2-3 presents approximate minimum ideal delta-V values in km/s. The values are relative to escape from the Sun on the horizontal axis, and escape from planets and some satellites and asteroids out to Jupiter on the vertical axis. The scales are different for the axes. Other tables and graphs can be found in the Delta-V Budget article, or calculated individually for particular missions.
There is no absolute reference frame for measuring velocity. This figure uses escape as the zero value. It has the physical meaning of "to leave this gravity well, you must add this much velocity". The term Gravity Well is used by analogy to water wells, as something you must climb out of to get away from it. Objects which have reached escape velocity are free to travel to other places. The Sun's surface is not as good a reference point since it can't be reached with known technology. Since velocity must be added to escape, the values are negative. If you have more than enough velocity to leave a gravity well, the amount remaining at great distances is called Excess Velocity.
Total Mission Velocity - is the sum of vertical and horizontal velocity changes on the diagram. To travel from Earth to Mars, for example, you first have to add velocity to climb out of the Earth's gravity well, add more velocity to change orbit within the Sun's gravity well, then subtract velocity to go down Mars' gravity well.
On the diagram that means following the vertical line from Earth's surface to the top line, which are Solar System orbits (11.18), plus the horizontal segment to go from the Earth's orbit to Mars' orbit (2.3), plus the vertical line to go to the Martian surface (5.03). That gives a total mission velocity of 18.5 km/s. This has to be provided by various propulsion, gravity assist, or drag maneuvers. To return to Earth, then reverse the steps.
The graph shows theoretical values (single impulse to escape). Real changes in velocity will be higher because (1) maneuvers are not perfectly efficient, (2) orbits are elliptical and inclined, and (3) losses such as atmospheric drag oppose the intended changes. Losses are measured by the difference between Ideal Velocity - what you would reach in a vacuum with no gravity well present, and the actual velocity you reach in a given circumstance. So this graph is not an exact method for mission planning. It is intended to give a rough estimate as a starting point for planning.
Velocity Bands - There are two velocity regions on the vertical axis for each planet or satellite. The lower sub-orbital region (thin blue line) is when there is enough velocity to get off the object, but not reach a stable orbit. Those orbits will intersect the surface again. They can be used to travel between points on the surface, but not to stay in motion for multiple orbits. The higher orbital band (thick blue line) indicates enough velocity for a repeating orbit. The shape of the orbit matters, but for circular orbits the lowest point in this band is an orbit just above the surface, and the highest point is an orbit just fast enough to escape from it's gravity well.
Gravity decreases as the square of distance. So large velocity changes are needed for small altitude changes near the surface. Conversely, near escape velocity, small velocity changes can produce large changes in altitude, and at escape it produces a theoretically infinite change. In reality there are multiple gravity wells that overlap, so escape from Earth merely places you in the larger solar gravity well, and escape from the Sun places you in the larger gravity well of the Galaxy.
Solar Orbits - The top blue line represents orbits around the Sun away from local gravity wells. The surface of the two largest asteroids, 4 Vesta (-0.35) and 1 Ceres (-0.51) are marked, but the orbital bands for these two asteroids, and the entire gravity well for most smaller asteroids, are too small to show. Instead, the range of solar velocities are shown with thick horizontal arrows for Near Earth Objects and the Main Belt Asteroids between Mars and Jupiter. The velocities of all small objects in the Solar System are spread across the entire top line. The two marked ranges just have particular interest. The surfaces of Jupiter and the Sun, and their sub-orbital ranges are off the scale of this chart because of their very deep gravity wells, and only inner and outer of Jupiter's four large moons are shown.

4.0 - Powered Flight
[edit | edit source]
Powered Flight involves trajectories and orbits influenced by artificial forces, in addition to natural ones. It originally applied to aircraft, but has been extended to space systems. Artificial forces can be produced internally, or applied from outside. The most common internal example is from chemical rocket engines. Examples of outside forces are a powerful laser applying light pressure to a target, and a stationary gun using high pressure gas to accelerate a projectile.
The powered part of a flight may last a short time, as when a rocket launches into orbit. After that it coasts, only affected by gravity and other natural forces. A solar-electric engine, on the other hand, may operate over most or all of a flight or mission.
4.1 - Ascent Trajectories
[edit | edit source]
Circular orbit velocity at the earth's surface is 7910 m/s. At the equator the Earth rotates eastward at 465 m/s. In theory a transport system has to provide the difference of 7445 m/s to reach orbit. For many transport methods, the Earth's atmosphere causes losses that add to the theoretical velocity needed. The design goal is to find the most efficient flight path, or Trajectory, that minimizes losses.
For chemical-powered Launch Vehicles on Earth, they normally fly straight up at first, so as to spend the least amount of time fighting atmospheric drag. The vertical velocity gained does not contribute to the orbit velocity, since they are perpendicular. What it does is help reach a final altitude where drag is minimal and stable orbits are possible. An optimized ascent trajectory rather quickly tilts from vertical towards the horizontal. Just enough climb is used to clear the atmosphere and minimize drag.
Gravity is opposing the vertical acceleration of a rocket. In the lower limit of thrust = weight, it does not move at all and all the propellant is wasted. When thrust is greater (>) than weight, only the surplus provides acceleration. Gravity Loss describes the difference in m/s a rocket actually gains vs what it would have gained if gravity was not present. Drag Loss similarly is the difference if the atmosphere were not present. Gaining enough altitude to be above significant atmosphere requires adding potential energy, which also requires consumes propellant.
The Ideal Velocity is what a rocket would gain in open space if none of these effects were present. This is the performance the propulsion system has to provide. The Real velocity is what it actually gains. A typical ideal velocity for rockets on Earth is about 9000 m/s to reach orbit. Losses are then about 1500 m/s, or a 20% more than the the real delta-V.
Mathematically, to go from a non-rotating body's surface to orbit requires that a rocket change its velocity from a rest velocity (zero) to a velocity that will keep the payload in orbit. The total velocity change is the integral over time of the acceleration a
where, T is thrust, m is the vehicle mass, L are other losses, and g is the component of gravity opposite thrust. All of these values can change during the ascent, so it is usually calculated with a computer using small time increments. On a rotating the starting velocity is whatever the local rotation velocity is rather than zero.
4.2 - Mass Ratio
[edit | edit source]
Rockets expel part of their mass at high velocity to produce thrust. The total ideal velocity change delta-V can be found from the Tsiolkovsky Rocket Equation, named after one of the people who independently derived it. Where exhaust velocity is ve, ln is the Natural Logarithm function, and the initial and final masses are m0 and m1, then
The difference between the initial and final masses represents the propellant or reaction mass used. The ratio of the initial and final masses is called the Mass Ratio, which for typical multi-stage rockets is in the range of 8 to 20. The final mass consists of the remaining vehicle hardware plus Payload mass. Payload is whatever items are intended to reach the desired orbit or destination. If the payload mass is set to zero, then a maximum delta-V is reached for the particular technology, and missions that require more than this are impossible.
4.3 - Staging
[edit | edit source]
A certain fraction of a vehicle's total initial mass will be its own hardware. From the above rocket equation there is a maximum velocity it can reach even with zero payload. When the required mission velocity is near or above this point, dropping some of the empty vehicle tanks and engines allows continued flight. A new mass ratio and delta-V starting from that point can be calculated from the remaining vehicle masses. This is known as Staging, and resulting design is a Multistage Rocket. The total ideal velocity is then the sum of the velocities that each stage produces.
The component stages are numbered in order of last use as first stage, second stage, etc. Last use is mentioned because stages can operate in parallel. The one to be dropped first gets the lower stage number. An example of this was the Space Shuttle, where the solid boosters operated in parallel with the Orbiter engines until the boosters were empty and were dropped. So the boosters were the first stage, and the Orbiter plus External Tank made up the second or upper stage.
The velocity to reach Earth orbit is approximately twice the exhaust velocity of the best liquid propellants in use. So the rocket equation yields a theoretical mass ratio of e2 or 7.39, and a final mass of 13.5%. This percentage is close to the hardware mass of typical designs, leaving no payload. So staging has commonly been used with rockets going to Earth orbit.
Vehicle design involves other factors besides optimizing mass ratio. One is economic efficiency in terms of cost per delivered payload mass. After all the design factors are included, most launch vehicles from Earth use two or three stages depending on what orbit they intend to reach.








