Social Statistics, Chapter 1: An Introduction to Social Statistics
An Introduction to Social Statistics
[edit | edit source]The children of rich parents usually grow up to be rich adults, and the children of poor parents usually grow up to be poor adults. This seems like a fundamental fact of social life, but is it true? And just how true is it? We've all heard stories of poor persons who make it rich (Oprah Winfrey, Jennifer Lopez, Steve Jobs) and rich persons who spend all their money and end up poor. The relationship between parents' income and children's income for a random sample of Americans is depicted in Figure 1-1. As you can see, parents' income and children's income are related, but with plenty of room for error. Rich parents tend to have rich children, but not all the time, and poor parents tend to have poor children, but not all the time. This kind of result is very common in the social sciences. Social science can explain a lot of things about our world, but it never explains them perfectly. There's always room for error.

The goal of social statistics is to explain the social world as simply as possible with as little error as possible. In Figure 1-1, it seems like parents' incomes explain their children's incomes pretty well, even if not perfectly. Some of the error in explaining children's incomes might come from errors in measurement. Persons don't always answer honestly when asked how much money they make. Persons might not even know for sure exactly how much money they made in any given year. It's impossible to predict the mistakes persons will make in answering social survey questions about their incomes, so no analysis of children's reported incomes will be perfectly accurate.
On the other hand, most of the error in Figure 1-1 probably has nothing to do with bad measurement. Most of the error is in explaining children's incomes probably comes from important determinants of income that have been left out of this analysis. There are many potential reasons why children's incomes may not correspond to their parents' incomes. For example, potential sources of error include things like:
- Children may do better / worse in school than their parents did
- Children may enter more / less well-paying professions than their parents did
- Children may be more / less lucky in getting a job than their parents were
- Children may be more / less ambitious than their parents were
A statistical analysis of income that included children's school performance, choice of profession, job luck, and ambition would have less error than the simple graph based just on parents' income, but it would also be much more complicated. Social statistics always involves trade-offs like this between complexity and error. Everything about the social world is determined by many different factors. A person's income level might result in part from job advice from a friend, getting a good recommendation letter, looking good on the day of an interview, being black, being female, speaking English with a strong accent, or a million other causes. Social statistics is all about coming up with ways to explain social reality reasonably well using just a few of these causes. No statistical model can explain everything, but if a model can explain most of the variability in persons' incomes based on just a few simple facts about them, that's pretty impressive.
This chapter lays out some of the basic building blocks of social statistics. First, social statistics is one of several approaches that social scientists use to link social theory to data about the world (Section 1.1). It is impossible to perform meaningful statistical analyses without first having some kind of theoretical viewpoint about how the world works. Second, social statistics is based on the analysis of cases and variables (Section 1.2). For any variable we want to study (like income), we have to have at least a few cases available for analysis—the more, the better. Third, social statistics almost always involves the use of models in which some variables are hypothesized to cause other variables (Section 1.3). We usually use statistics because we believe that one variable causes another, not just because we're curious. An optional section (Section 1.4) tackles the question of just how causality can be established in social statistics.
Finally, this chapter ends with an applied case study of the relationship between spending on education and student performance across the 50 states of the United States (Section 1.5). This case study illustrates how theory can be applied to data, how data are arranged into cases and variables, and how independent and dependent variables are causally related. All of this chapter's key concepts are used in this case study. By the end of this chapter, you should have all the tools you need to start modeling the social world using social statistics.
1.1: Theory and Data
[edit | edit source]Theories determine how we think about the social world. All of us have theories about how the world works. Most of these theories are based on personal experience. That's alright: Isaac Newton is supposed to have developed the theory of gravity because he personally had an apple fall on his head. Personal experience can be a dangerous guide to social theory, since your experiences might be very difference from other persons' experiences. It's not a bad place to start, but social science requires that personal experiences be turned into more general theories that apply to other persons as well, not just to you. Generalization is the act of turning theories about specific situations into theories that apply to many situations. So, for example, you may think that you eat a lot of junk food because you can't afford to eat high-quality food. This theory about yourself could be generalized into a broader theory about persons in general:
- Persons eat junk food because they can't afford to eat high-quality food.
Generalization from personal experience is one way to come up with theories about the social world, but it's not the only way. Sometimes theories come from observing others: you might see lots of fast food restaurants in poor neighborhoods and theorize that persons eat junk food because they can't afford to eat high-quality food. Sometimes theories are developed based on other theories: you might theorize that all persons want to live as long as possible, and thus conclude that persons eat junk food because they can't afford to eat high-quality food. Sometimes ideas just pop into your head: you're at a restaurant drinking a soda with unlimited free refills, and it just dawns on you that maybe persons eat junk food because they can't afford to eat high-quality food. However it happens, somehow you conceive of a theory. Conceptualization is the process of developing a theory about some aspect of the social world.
The main difference between the kinds of social commentary you might hear on radio or television and real social science is that in social science theories are scrutinized using formal statistical models. Statistical models are mathematical simplifications of the real world. The goal of statistical modeling is to explain complex social facts as simply as possible. A statistical model might be as simple as a graph showing that richer parents have richer children, as depicted in Figure 1-1. This graph is takes a very complex social fact (children's income) and explains it in very simple terms (it rises as parents' income rises) but with lots of room for error (many children are richer or poorer than their parents).
Social scientists use statistical models to evaluate different theories about how the world works. In our minds we all have our own theories about the social world, but in the real world we can't all be right. Before social scientists accept a theory, they carefully evaluate it using data about the real world. Before they can be evaluated, theories have to be turned into specific hypotheses about specific data. Operationalization is the process of turning a social theory into specific hypotheses about real data. The theory that persons eat junk food because they can't afford to eat high-quality food seems very reasonable, but it's too vague to examine using social statistics. First it has to be operationalized into something much more specific. Operationalization means answering questions like:
- Which persons eat junk food? All persons in the world? All Americans? Poor Americans only?
- What's junk food? Soda? Candy? Potato chips? Pizza? Sugar cereals? Fried chicken?
- What's high-quality food? Only salads and home-made dinners? Or do steaks count too?
- Is fresh-squeezed fruit juice a junk food (high in sugar) or a high-quality food (fresh and nutritious)?
- What does "afford" mean? Literally not having enough money to buy something? What about other expenses besides food?
- Whose behavior should we study? Individuals? Families? Households? Whole cities? Counties? States? Countries? The world?
For example, one way to study the relationship between junk food consumption and the affordability of high-quality food is to use state-level data. It can be very convenient to study US states because they are similar in many ways (they're all part of the same country) but they are also different enough to make interesting comparisons. There is also a large amount of data available for US states that is collected and published by US government agencies. For example, junk food consumption can be operationalized as the amount of soft drinks or sweetened snacks consumed in the states (both available from the US Department of Agriculture) and affordability can be operationalized using state median income. Most persons living in states with high incomes should be able to afford to eat better-quality food.
Data on state soft drink consumption per person and state median income are graphed in Figure 1-2. Each point in Figure 1-2 represents a state. A few sample states are labeled on the graph. This graph is called a scatter plot. Scatter plots are very simple statistical models that depict data on a graph. The scatter plot can be used to determine whether soft drink consumption rises, falls, or stays the same across the range of state income levels. In the scatter plot graphed in Figure 1-2, soft drink consumption tends to fall as income rises. This is consistent with the theory that persons buy healthy food when they can afford it, but eat unhealthy food when they are poorer. The theory may or may not be correct. The scatter plot provides evidence in support of the theory, but it does not conclusively prove the theory. After all, there may be many other reasons why soft drink consumption tends to be higher in the poorer states.
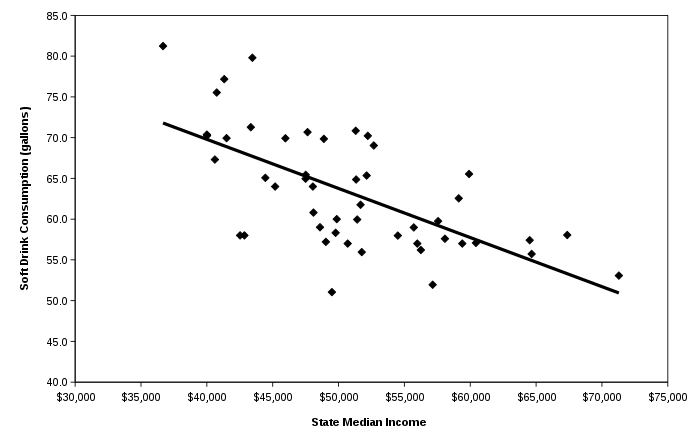
There is also a lot of error in the statistical model explaining soft drink consumption. There are many poor states that have very low levels of soft drink spending as well as many rich states that have very high levels of soft drink spending. So while the overall trend is that richer states have lower spending on soft drinks, there are many exceptions. This could be because the theory is wrong, but it also could be because there are many reasons why persons might consume soft drinks besides the fact that they are poor. For example, persons might consume soft drinks because:
- They live in places with hot weather and consume a lot of all kinds of drinks
- They eat out a lot, and tend to consume soft drinks at restaurants
- They're trying to lose weight and are actually consuming zero-calorie soft drinks
- They just happen to like the taste of soft drinks
All these reasons (and many others) may account for the large amount of error in the statistical model graphed in Figure 1-2.
Another way to operationalize the theory that theory that persons eat junk food because they can't afford to eat high-quality food is presented in Figure 1-3. In Figure 1-3, junk food consumption is operationalized as consumption of sweetened snack foods (cookies, snack cakes, candy bars, and the like). Again, the overall theory is that persons eat junk food because they can't afford to eat high-quality food, so state average income should be negatively related to the consumption of sweetened snack foods. In other words, as state average income goes up, sweetened snack food consumption should go down. But the data tell a different story: it turns out that there is essentially no relationship between state average income and sweetened snack consumption.

What went wrong here? Why is there no relationship between state average income and sweetened snack consumption? There are many possible reasons.
First, it may have been wrong to generalize from one person's experience (I eat junk food because I can't afford to eat high-quality food) to a general rule about society (persons eat junk food because persons can't afford to eat high-quality food). Second, it may have been wrong to conceptualize any relationship between affordability and junk food consumption at all (maybe junk food is actually more expensive than high-quality food). Third, it may have been wrong to operationalize junk food consumption at the state level (for example, it is possible that rich states actually contain lots of poor persons who eat lots of sweetened snacks). Fourth, it may have been wrong to use such a simple statistical model as a scatter plot (later chapters in this book will present much more sophisticated statistical models).
Because there are so many possible sources of error in social statistics, statistical analyses often lead to conflicting results like those reported in Figure 1-2 and Figure 1-3. Inconsistent, inconclusive, or downright meaningless results pop up all the time. The social world is incredibly complicated. Social theories are always far too simple to explain it all. Social statistics give us the opportunity to see just how well social theories perform out in the real world. In the case of our theory that persons eat junk food because they can't afford to eat high-quality food, social statistics tell us that there is some evidence to support the theory (soft drink consumption tends to be higher in poor states), but better theories are clearly needed to fully explain differences in persons' junk food consumption.
1.2: Cases and Variables
[edit | edit source]As the junk food example shows, when operationalizing theories into specific hypotheses in the social sciences the biggest obstacle is usually the difficulty of getting the right the data. Few quantitative social scientists are able to collect their own data, and even when they do they are often unable to collect the data they want. For example, social scientists who want to study whether or not persons can afford to buy high-quality food would ideally want to know all sorts of things to determine affordability. They would want to know persons' incomes, of course, but they would also want to know how much healthy foods cost in each person's neighborhood, how far persons would have to drive to get to a farm store or organic supermarket, whether or not they have a car, how many other expenses persons have besides food, etc. Such detailed information can be very difficult to collect, so researchers often make do with just income.
It is even more difficult to find appropriate data when researchers have to rely on data collected by others. The collection of social data is often done on a very large scale. For example, most countries conduct a population census at regular intervals. In the United States, this involves distributing short census questionnaires to over 100 million households every ten years. The longer, more detailed American Community Survey is sent to around 250,000 households every month. A further 60,000 households receive a detailed employment survey, the Current Population Survey. Other social data can also be very difficult and expensive to collect. The income data used in Figure 1-2 come from a national survey of 12,686 persons and their children who were surveyed almost every year for thirty years. The food consumption data used in Figures 1-2 and 1-3 come from barcode scans of products bought by 40,000 households across America. Obviously, no one person can collect these kinds of data on her own.
The good news is that enormous amounts of social survey and other social data can now be downloaded over the internet. All the data used in this textbook are freely available to the public from government or university websites. These public use datasets have been stripped of all personally identifying information like the names and addresses of individual respondents. Also very conveniently, the data in these datasets have usually been organized into properly formatted databases.
Databases are arrangements of data into variables and cases. When persons are interviewed in a survey, the raw data often have to be processed before they can be used. For example, surveys don't usually ask persons their ages, because (believe it or not) persons often get their ages wrong. Instead, survey takers ask persons their dates of birth. They also record the date of the survey. These two dates can then be combined to determine the respondent's age. The respondent's age is a sociologically meaningful fact about the respondent. Raw data like the respondent's birth date and interview date have been transformed into a variable that can be used in statistical models.
Variables are analytically meaningful attributes of cases. Cases are the individuals or entities about which data have been collected. Databases usually include one row of data for each case. Variables are arranged into columns. There may also be columns of metadata. Metadata are additional attributes of cases that are not meant to be included in analyses. A sample database including both metadata and variables is presented in Figure 1-4.
| STATE_NAME | STATE_ABBR | MED_INCOME | LB_SNACKS | GAL_SODA | LB_FRUVEG | |
|---|---|---|---|---|---|---|
| Alabama | AL | $40,751 | 111.6 | 75.5 | 168.3 | |
| Arizona | AZ | $49,863 | 109.0 | 60.0 | 157.0 | |
| Arkansas | AR | $40,001 | 104.3 | 70.4 | 147.3 | |
| California | CA | $58,078 | 105.7 | 57.6 | 201.8 | |
| Colorado | CO | $57,559 | 109.2 | 59.8 | 159.2 | |
| Connecticut | CT | $64,662 | 131.5 | 55.7 | 188.1 | |
| Delaware | DE | $56,252 | 134.6 | 56.2 | 218.2 | |
| District of Columbia | DC | $50,695 | 122.0 | 57.0 | 218.2 | |
| Florida | FL | $48,095 | 104.4 | 60.8 | 168.8 | |
| Georgia | GA | $51,673 | 107.1 | 61.8 | 198.4 | |
| Idaho | ID | $49,036 | 130.0 | 57.2 | 185.3 | |
| Illinois | IL | $52,677 | 127.8 | 69.0 | 198.0 | |
| Indiana | IN | $47,647 | 122.3 | 70.7 | 184.5 | |
| Iowa | IA | $51,339 | 121.1 | 64.9 | 171.2 | |
| Kansas | KS | $47,498 | 120.9 | 65.0 | 170.8 | |
| Kentucky | KY | $41,320 | 144.7 | 77.2 | 170.7 | |
| Louisiana | LA | $40,016 | 101.9 | 70.2 | 147.1 | |
| Maine | ME | $48,592 | 118.0 | 59.0 | 190.0 | |
| Maryland | MD | $67,364 | 125.1 | 58.0 | 218.5 | |
| Massachusetts | MA | $60,434 | 116.8 | 57.1 | 155.6 | |
| Michigan | MI | $51,305 | 122.5 | 70.8 | 181.2 | |
| Minnesota | MN | $59,910 | 120.5 | 65.5 | 172.8 | |
| Mississippi | MS | $36,674 | 112.5 | 81.2 | 160.2 | |
| Missouri | MO | $47,507 | 120.6 | 65.4 | 172.3 | |
| Montana | MN | $42,524 | 111.0 | 58.0 | 175.0 | |
| Nebraska | NE | $52,134 | 120.6 | 65.3 | 172.4 | |
| Nevada | NV | $54,500 | 111.5 | 58.0 | 175.3 | |
| New Hampshire | NH | $64,512 | 115.6 | 57.4 | 159.0 | |
| New Jersey | NJ | $71,284 | 135.8 | 53.1 | 201.1 | |
| New Mexico | NM | $42,850 | 111.0 | 58.0 | 175.0 | |
| New York | NY | $51,763 | 111.5 | 56.0 | 184.9 | |
| North Carolina | NC | $44,441 | 104.6 | 65.1 | 165.7 | |
| North Dakota | ND | $45,184 | 122.0 | 64.0 | 169.0 | |
| Ohio | OH | $48,884 | 122.6 | 69.8 | 185.0 | |
| Oklahoma | OK | $41,497 | 103.6 | 69.9 | 143.2 | |
| Oregon | OR | $49,495 | 111.0 | 51.0 | 173.8 | |
| Pennsylvania | PA | $51,416 | 130.0 | 60.0 | 203.7 | |
| Rhode Island | RI | $55,980 | 115.0 | 57.0 | 151.0 | |
| South Carolina | SC | $43,338 | 100.5 | 71.3 | 161.5 | |
| South Dakota | SD | $48,051 | 122.0 | 64.0 | 169.0 | |
| Tennessee | TN | $43,458 | 113.9 | 79.8 | 167.4 | |
| Texas | TX | $45,966 | 104.7 | 69.9 | 162.0 | |
| Utah | UT | $59,395 | 135.0 | 57.0 | 188.0 | |
| Vermont | VE | $55,716 | 117.8 | 59.0 | 187.1 | |
| Virginia | VA | $59,126 | 110.5 | 62.6 | 187.7 | |
| Washington | WA | $57,148 | 111.9 | 51.9 | 175.0 | |
| West Virginia | WV | $40,611 | 107.4 | 67.3 | 176.0 | |
| Wisconsin | WI | $52,223 | 121.3 | 70.2 | 183.9 | |
| Wyoming | WY | $49,777 | 114.0 | 58.3 | 172.7 |
The database depicted in Figure 1-4 was used to conduct the analyses reported in Figure 1-2 and Figure 1-3. The first two columns in the database are examples of metadata: the state name (STATE_NAME) and state abbreviation (STATE_ABBR). These are descriptive attributes of the cases, but they are not analytically meaningful. For example, we would not expect soda consumption to be determined by a state's abbreviation. The last four columns in the database are examples of variables. The first variable (MED_INCOME) is each state's median income. The other three variables represent annual state sweetened snack consumption in pounds per person (LB_SNACKS), soft drink consumption in gallons per person (GAL_SODA), and fruit and vegetable consumption in pounds per person (LB_FRUVEG). As in Figure 1-4, metadata are usually listed first in a database, followed by variables. The cases are usually sorted in order using the first metadata column as a case identifier. In this case, the data are sorted in alphabetical order by state name.
The cases in a database can be political units (like states or countries), organizations (like schools or companies), persons (like individuals or families), or any other kind of entity. The database that was used in Figure 1-1 is presented in Figure 1-5. In this database, the metadata appear in the first column (CHILD_ID) and the fifth column (MOTHER_ID). The gender of each child is reported in the third column (GENDER). Gender is recorded as "1" for men and "2" for women and mother's race is recorded as "1" for white and "2" for non-white. Income variables for the children's families (FAM_INC) and their mothers' families (PAR_INC) appear in the second and fifth columns. Notice that the incomes of the children's families are rounded off, while the incomes of the mothers' families are exact. Researchers using these data have to accept inconsistencies like this and work with them, since there's no way to go back and re-collect the data. We're stuck using the data as they exist in the database.
| CHILD_ID | FAM_INC | GENDER | M_RACE | MOTH_ID | PAR_INC |
|---|---|---|---|---|---|
| 2001 | $150,000 | 2 | 1 | 20 | $113,750 |
| 4902 | $90,000 | 1 | 1 | 49 | $90,090 |
| 23102 | $120,000 | 2 | 1 | 231 | $85,811 |
| 25202 | $68,000 | 1 | 1 | 252 | $13,679 |
| 55001 | $61,000 | 2 | 1 | 550 | $71,344 |
| 76803 | $100,000 | 2 | 1 | 768 | $56,784 |
| 82802 | $50,000 | 1 | 1 | 828 | $64,246 |
| 97101 | $59,000 | 2 | 1 | 971 | $32,396 |
| 185301 | $150,000 | 1 | 1 | 1853 | $176,904 |
| 226801 | $10,000 | 2 | 2 | 2268 | $3,786 |
| 236901 | $100,000 | 1 | 1 | 2369 | $182,002 |
| 294903 | $150,000 | 2 | 1 | 2949 | $62,062 |
| 302301 | $388,387 | 2 | 1 | 3023 | $120,120 |
| 315101 | $60,000 | 2 | 1 | 3151 | $37,310 |
| 363502 | $150,000 | 2 | 1 | 3635 | $64,370 |
| 385101 | $40,000 | 1 | 1 | 3851 | $70,980 |
| 396204 | $100,000 | 1 | 1 | 3962 | $62,972 |
| 402803 | $80,000 | 1 | 1 | 4028 | $111,202 |
| 411001 | $75,000 | 1 | 1 | 4110 | $10,804 |
| 463102 | $75,000 | 2 | 1 | 4631 | $61,880 |
| 463801 | $25,000 | 1 | 1 | 4638 | $25,859 |
| 511403 | $180,000 | 1 | 1 | 5114 | $105,196 |
| 512302 | $70,000 | 2 | 1 | 5123 | $41,860 |
| 522402 | $50,000 | 2 | 1 | 5224 | $43,680 |
| 542402 | $100,000 | 1 | 1 | 5424 | $35,736 |
| 548301 | $30,000 | 1 | 2 | 5483 | $46,279 |
| 552601 | $40,000 | 2 | 1 | 5526 | $30,940 |
| 576601 | $28,000 | 1 | 2 | 5766 | $21,849 |
| 581101 | $40,000 | 2 | 2 | 5811 | $72,800 |
| 611601 | $80,000 | 2 | 2 | 6116 | $30,940 |
| 616802 | $50,000 | 1 | 2 | 6168 | $11,102 |
| 623801 | $50,000 | 2 | 2 | 6238 | $26,426 |
| 680702 | $45,000 | 1 | 2 | 6807 | $27,300 |
| 749801 | $90,000 | 1 | 2 | 7498 | $43,680 |
| 757802 | $90,000 | 1 | 2 | 7578 | $30,940 |
| 761702 | $5,000 | 2 | 2 | 7617 | $8,008 |
| 771002 | $44,000 | 1 | 2 | 7710 | $9,218 |
| 822603 | $150,000 | 2 | 2 | 8226 | $180,726 |
| 825902 | $36,000 | 2 | 2 | 8259 | $20,457 |
| 848803 | $100,000 | 2 | 2 | 8488 | $79,549 |
| 855802 | $32,000 | 2 | 2 | 8558 | $7,280 |
| 898201 | $60,000 | 1 | 2 | 8982 | $13,523 |
| 906302 | $11,000 | 2 | 2 | 9063 | $9,218 |
| 943401 | $20,000 | 1 | 2 | 9434 | $7,571 |
| 977802 | $150,000 | 1 | 2 | 9778 | $96,460 |
| 1002603 | $32,000 | 2 | 2 | 10026 | $30,476 |
| 1007202 | $52,000 | 2 | 2 | 10072 | $17,734 |
| 1045001 | $60,000 | 2 | 2 | 10450 | $78,315 |
| 1176901 | $30,000 | 2 | 1 | 11769 | $66,375 |
| 1200001 | $80,000 | 1 | 1 | 12000 | $70,525 |
Each case in this database is an extended family built around a mother–child pair. The children's family incomes include the incomes of their spouses, and the mothers' family incomes include the incomes of their spouses, but the mothers' spouses may or may not be the fathers of the children in the database. Since the data were collected on mother–child pairs, we have no way to know the incomes of the children's biological fathers unless they happen to have been married to the mothers in 1987 when the mothers' income data were collected. Obviously we'd like to know the children's fathers' incomes levels, but the data were never explicitly collected. If the parents were not married as of 1987, the biological fathers' data are gone forever. Data limitations like the rounding off of variables and the fact that variables may not include all the data we want are major sources of error in statistical models.
1.3: Dependent Variables and Independent Variables
[edit | edit source]In social statistics we're usually interested in using some variables to explain other variables. For example, in operationalizing the theory that persons eat junk food because they can't afford to eat high-quality food we used the variable "state median income" (MED_INCOME) in a statistical model (specifically, a scatter plot) to explain the variable "soft drink consumption" (GAL_SODA). In this simple model, we would say that soft drink consumption depends on state median income. Dependent variables are variables that are thought to depend on other variables in a model. They are outcomes of some kind of causal process. Independent variables are variables that are thought to cause the dependent variables in a model. It's easy to remember the difference. Dependent variables depend. Independent variables are independent; they don't depend on anything.
Whether a variable is independent or dependent is a matter of conceptualization. If a researcher thinks that one variable causes another, the cause is the independent variable and the effect is the dependent variable. The same variable can be an independent variable in one model but a dependent variable in another. Within any one particular model, however, it should be clear which variables are independent and which variables are dependent. The same variable can't be both: a variable can't cause itself.
For an example of how a variable could change from independent to dependent, think back to Figure 1-1. In that figure, parents' income is the independent variable and children's income is the dependent variable (in the model, parents' income causes children's income). Parents' income, however, might itself be caused by other variables. We could operationalize a statistical model in which the parents' family income (the variable PAR_INC) depends on the parents' race (M_RACE). We use the mother's race to represent the race of both parents, since we don't have data for each mother's spouse (if any). A scatter plot of parents' family income by race is presented in Figure 1-6. Remember that the variable M_RACE is coded so that 0 = white and 1 = non-white. Clearly, the white parents had much higher family incomes (on average) than the non-white parents, almost twice as high. As with any statistical model, however, there is still a lot of error: race explains a lot in America, but it doesn't explain everything.
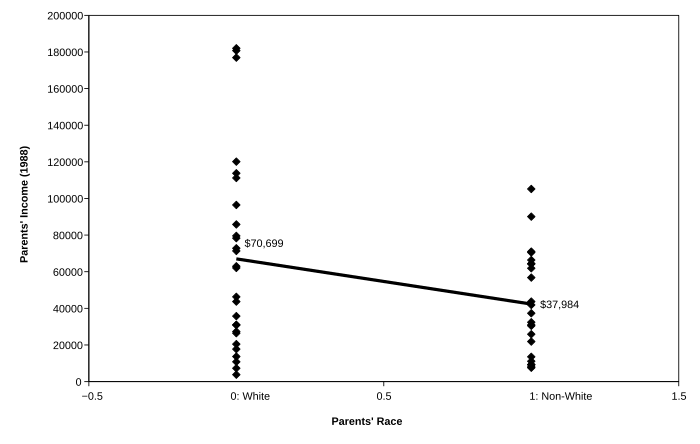
Just like parents' income, any variable can be either an independent variable or a dependent variable. It all depends on the context. All of the dependent variables and independent variables that have been used so far in this chapter are summarized in Figure 1-7. An arrow (→) has been used to indicate which variable is thought to cause which. Remember, in each model the independent variable causes the dependent variable. That's the same as saying that the dependent variables depend on the independent variables. Since parents' income has been used as both an independent variable (Figure 1-1) and as a dependent variable (Figure 1-6) it appears twice in the table. State median income has also been used twice, both times as an independent variable (Figure 1-2 and Figure 1-3).
| Figure | Independent Variable | Dependent Variable | Model | Trend |
|---|---|---|---|---|
| Figure 1-1 | Parents' income → | Children's income | Scatter plot | Up |
| Figure 1-2 | State median income → | Soft drink consumption | Scatter plot | Down |
| Figure 1-3 | State median income → | Sweetened snack consumption | Scatter plot | Up |
| Figure 1-6 | Parents' race → | Parents' income | Scatter plot | Down |
In each example reported in Table 1-1, the statistical model used to understand the relationship between the independent variable and the dependent variable has been a scatter plot. In a scatter plot, the independent variable is always depicted on the horizontal (X) axis. The dependent variable is always depicted on the vertical (Y) axis. A line has been drawn through the middle of the cloud of points on each scatter plot to help illustrate the general trend of the data. In Figure 1-1 the general trend is up: parents' income is positively related to children's income. In Figure 1-2 the general trend is down: state median income is negatively related to soft drink consumption. In Figure 1-3 and Figure 1-6 the trends are again up and down, respectively. Whether the trend is up or down, the existence of a trend indicates a relationship between the independent variable and the dependent variable.
A scatter plot is a very simple statistical model that helps show the overall relationship between one independent variable and one dependent variable. In future chapters, we will study more sophisticated statistical models. Many of them will allow for multiple independent variables of different kinds, but every model used in this book will have just one dependent variable. Models with multiple dependent variables exist, but they are much more complicated and won't be covered here.
1.4: Inferring Causality
[edit | edit source]- Optional/advanced
Social scientists are almost always interested in making claims about causality, in claiming that one variable causes another. We suspect that sexism in the workplace leads to lower wages for women, that education leads to greater life fulfillment, that social inequality leads to higher levels of violence in society. The problem is that in the social sciences it is almost always impossible to prove that one variable causes another. Instead, social scientists must infer causality as best they can using the facts—and reasoning—at their disposal.
It is so difficult to establish causality in the social sciences because most social science questions cannot be studied using experiments. In an experiment, research subjects are randomly assigned to two groups, an experimental group and a control group. The subjects in the experimental group receive some treatment, while the subjects in the control group receive a different treatment. At the end of the experiment, any systematic difference between the subjects in the two groups must be due to differences in their treatments, since the two groups have otherwise identical backgrounds and experiences.
In the social sciences, experiments are usually impossible. For example, we strongly suspect that sexism in the workplace causes lower wages for women. The only way to know for sure whether or not this is true would be to recruit a group of women and randomly assign them to work in different workplaces, some of them sexist and some of them not. The workplaces would have to be identical, except for the sexism. Then, after a few years, we could call the women back to check up on their wages. Any systematic differences in women's wages between those who worked in sexist workplaces and those who worked in non-sexist workplaces could then be attributed to the sexism, since we would know for certain that there were no other systematic differences between the groups and their experiences.
Of course, experiments like this are impossible. As a substitute for experiments, social scientists conduct interviews and surveys. We ask women whether or not they have experienced sexism at work, and then ask them how much money they make. If the women who experience sexism make less money than the women who do not experience sexism, we infer that perhaps that difference may be due to actual sexism in the workplace.
Social scientists tend to be very cautious in making causal inferences, however, because many other factors may be at work. For example, it is possible that the women in the study who make less money tend incorrectly to perceive their workplaces as being sexist (reverse causality). It is even possible that high-stress working environments in which persons are being laid off result both in sexist attitudes among managers and in lower wages for everyone, including women (common causality). Many other alternatives are also possible. Causality is very difficult to establish outside the experimental framework.
Most social scientists accept three basic conditions that, taken together, establish that an independent variable actually causes a dependent variable. They are:
- Correlation: when the independent variable changes, the dependent variable changes
- Precedence: the independent variable logically comes before the dependent variable
- Non-spuriousness: the independent variable and the dependent variable are not both caused by some other factor
Of the three conditions, correlation is by far the easiest to show. All of the scatter plots depicted in this chapter demonstrate correlation. In each case, the values of the dependent variable tends to move in one direction (either up or down) in correspondence with values of the independent variable.
Precedence can also be easy to demonstrate—sometimes. For example, in Figure 1-6 it is very clear that race logically comes before income. It wouldn't make any sense to argue the opposite, that persons' incomes cause their racial identities. At other times precedence can be much more open to debate. For example, many development sociologists argue that universal education leads to economic development: an educated workforce is necessary for development. It is possible, however, that the opposite is true, that economic development leads to universal education: when countries are rich enough to afford it, they pay for education for all their people. One of the major challenges of social policy formation is determining the direction of causality connecting variables.
Non-spuriousness, on the other hand, is almost always very difficult to establish. An observed relationship between two variables is called "spurious" when it doesn't reflect any real connection between the variables. For example, smoking tobacco can cause lung cancer and smoking tobacco can cause bad breath, but bad breath doesn't cause lung cancer. This general logic of spuriousness is depicted in Figure 1-8. In Figure 1-8, a spurious relationship exists between two variables in a statistical model. The real reason for the observed correlation between the independent variable and the dependent variable is that both are caused by a third, common-cause variable. Situations like this are very common in the social sciences. In order to be able to claim that one variable causes another, a social scientist must show that an observed relationship between the independent variable and the dependent variable is not spurious.
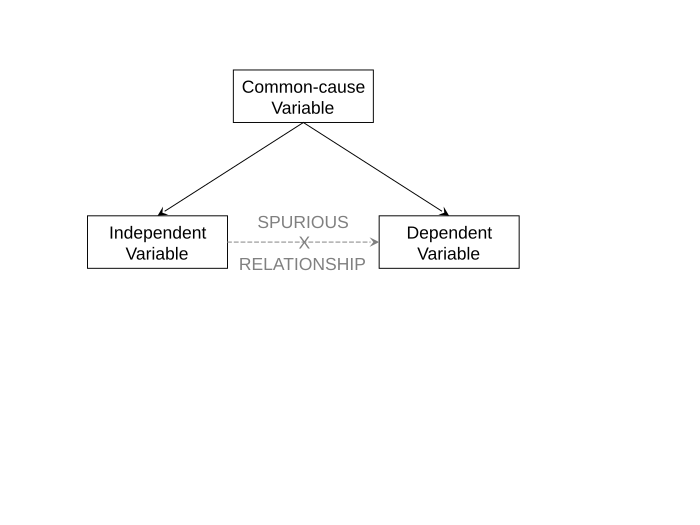
The problem with demonstrating non-spuriousness is that there can be many possible reasons why a relationship might be spurious. Returning to the relationship between parents' income and children's income, it is easy to see that there is a correlation between the two variables (Figure 1-1). It is also pretty obvious that parents' income precedes children's income. But what about non-spuriousness? There are many reasons why the relationship between parents' income and children's income might be spurious. One we've already seen: race. Non-white parents tend to have non-white children, so it's possible that instead of parent's income causing children's income, the truth is that the family's race determines both the parents' and the children's incomes (race is a common-cause variable). This could account for the observed correlation between parents' income and children's income. Other possible common-cause variables include:
- The family's area of residence
- The degree to which the family values money-making
- Parents' educational levels (which can influence children's educational choices)
- The parents' number of children
This last common-cause variable is an instructive example. In theory, having large numbers of children could force parents to stay home instead of working, lowering their incomes and making it difficult for them to afford college educations for their children, who could then have lower incomes as well. This might seem to most reasonable persons like a very unlikely scenario. The problem is that different persons have different ideas about what is reasonable. In order to establish the non-spuriousness of a relationship, researchers don't just have to convince themselves. They have to convince others, and everyone has a different idea of what might possibly create a spurious relationship between two variables. In the end, it is impossible to prove non-spuriousness. Instead, social scientists argue until they reach a consensus—or they just keep arguing. Causality is always subject to debate.
1.5: Case Study: Education Spending and Student Performance
[edit | edit source]Everyone knows that there are good schools and there are bad schools. The first question most parents ask when they're looking at a new home is "how are the schools?" Common sense suggests that the good schools are, on average, the rich schools. Everyone wants their children to go to schools that have brand-new computer labs, impressive sports facilities, freshly painted hallways, and nice green lawns. Parents also want their kids to receive individualized attention in small classes taught by talented, experienced teachers with master's degrees and doctorates. Active band, chorus, and art programs are also a plus. All this takes money.
A reasonable generalization from the observation that parents want to send their kids to schools that cost a lot of money to run is that states that spend more money on education will have better schools than states that spend less money on education. This generalization can be conceptualized into the theory that overall student performance depends (at least in part) on the amount of money a state spends on each student. This theory can be examined using data from the US National Center for Education Statistics (NCES). A database downloaded from the NCES website is reproduced in Figure 1-9. The cases are the 50 US states. There are two metadata columns (STATE and ABBR) and three variables (SPEND, READ_NAT, and MATH):
SPEND– Total state and local education spending per pupilREAD_NAT– State-average reading scores for native English-speaking 8th grade studentsMATH– State-average math scores for all 8th grade students
| STATE | ABBR | SPEND | READ_NAT | MATH |
|---|---|---|---|---|
| Alabama | AL | $10,356 | 255.5 | 268.5 |
| Alaska | AK | $17,471 | 263.7 | 283.0 |
| Arizona | AZ | $9,457 | 260.8 | 277.3 |
| Arkansas | AR | $9,758 | 258.9 | 276.0 |
| California | CA | $11,228 | 261.5 | 270.4 |
| Colorado | CO | $10,118 | 268.5 | 287.4 |
| Connecticut | CT | $16,577 | 272.8 | 288.6 |
| Delaware | DE | $13,792 | 265.6 | 283.8 |
| District of Columbia | DC | $17,394 | 243.2 | 253.6 |
| Florida | FL | $10,995 | 265.3 | 279.3 |
| Georgia | GA | $11,319 | 260.9 | 277.6 |
| Hawaii | HI | $14,129 | 256.9 | 273.8 |
| Idaho | ID | $7,965 | 266.4 | 287.3 |
| Illinois | IL | $12,035 | 265.6 | 282.4 |
| Indiana | IN | $11,747 | 266.1 | 286.8 |
| Iowa | IA | $11,209 | 265.6 | 284.2 |
| Kansas | KS | $11,805 | 268.4 | 288.6 |
| Kentucky | KY | $9,848 | 267.0 | 279.3 |
| Louisiana | LA | $11,543 | 253.4 | 272.4 |
| Maine | ME | $13,257 | 267.9 | 286.4 |
| Maryland | MD | $15,443 | 267.5 | 288.3 |
| Massachusetts | MA | $15,196 | 274.5 | 298.9 |
| Michigan | MI | $11,591 | 262.4 | 278.3 |
| Minnesota | MN | $12,290 | 271.8 | 294.4 |
| Mississippi | MS | $8,880 | 251.5 | 265.0 |
| Missouri | MO | $11,042 | 267.0 | 285.8 |
| Montana | MT | $10,958 | 271.4 | 291.5 |
| Nebraska | NE | $11,691 | 267.8 | 284.3 |
| Nevada | NV | $10,165 | 257.4 | 274.1 |
| New Hampshire | NH | $13,019 | 271.0 | 292.3 |
| New Jersey | NJ | $18,007 | 272.9 | 292.7 |
| New Mexico | NM | $11,110 | 258.5 | 269.7 |
| New York | NY | $19,081 | 266.0 | 282.6 |
| North Carolina | NC | $8,439 | 261.1 | 284.3 |
| North Dakota | ND | $11,117 | 269.5 | 292.8 |
| Ohio | OH | $12,476 | 268.8 | 285.6 |
| Oklahoma | OK | $8,539 | 260.4 | 275.7 |
| Oregon | OR | $10,818 | 267.8 | 285.0 |
| Pennsylvania | PA | $13,859 | 271.2 | 288.3 |
| Rhode Island | RI | $15,062 | 261.3 | 277.9 |
| South Carolina | SC | $10,913 | 257.5 | 280.4 |
| South Dakota | SD | $9,925 | 270.4 | 290.6 |
| Tennessee | TN | $8,535 | 261.3 | 274.8 |
| Texas | TX | $9,749 | 263.2 | 286.7 |
| Utah | UT | $7,629 | 267.2 | 284.1 |
| Vermont | VT | $16,000 | 272.6 | 292.9 |
| Virginia | VA | $11,803 | 266.6 | 286.1 |
| Washington | WA | $10,781 | 268.7 | 288.7 |
| West Virginia | WV | $11,207 | 254.9 | 270.4 |
| Wisconsin | WI | $12,081 | 266.7 | 288.1 |
| Wyoming | WY | $18,622 | 268.6 | 286.1 |
The theory that overall student performance depends on the amount of money a state spends on each student can be operationalized into two specific hypotheses:
- State spending per pupil is positively related to state average reading scores
- State spending per pupil is positively related to state average mathematics scores
In Figure 1-10 and Figure 1-11, scatter plots are used as statistical models for relating state spending to state reading and math scores. The dependent variable in Figure 1-10 is READ_NAT (reading performance for native English-speaking students) and the dependent variable in Figure 1-11 is MATH (mathematics performance). The independent variable in both figures is SPEND. In both figures state average scores do tend to be higher in states that spend more, but there is a large amount of error in explaining scores. There are probably many other determinants of student test scores besides state spending. Scores might be affected by things like parental education levels, family income levels, levels of student drug abuse, and whether or not states "teach to the test" in an effort to artificially boost results. Nonetheless, it is clear that (on average) the more states spend, the higher their scores.


The results of these data analyses tend to confirm the theory that overall student performance depends (at least in part) on the amount of money a state spends on each student. This theory may or may not really be true, but the evidence presented here is consistent with the theory. The results suggest that if states want to improve their student test scores, they should increase their school budgets. In education, as in most things, you get what you pay for.
Chapter 1 Key Terms
[edit | edit source]- Conceptualization is the process of developing a theory about some aspect of the social world.
- Cases are the individuals or entities about which data have been collected.
- Databases are arrangements of data into variables and cases.
- Dependent variables are variables that are thought to depend on other variables in a model.
- Generalization is the act of turning theories about specific situations into theories that apply to many situations.
- Independent variables are variables that are thought to cause the dependent variables in a model.
- Metadata are additional attributes of cases that are not meant to be included in analyses.
- Operationalization is the process of turning a social theory into specific hypotheses about real data.
- Scatter plots are very simple statistical models that depict data on a graph.
- Statistical models are mathematical simplifications of the real world.
- Variables are analytically meaningful attributes of cases.