Simulation with AnyLogic/System Dynamics/Step 11. Modeling replacement purchases
Step 11. Modeling Replacement Purchases
The model we have created does not capture situations where the product is consumed, discarded, or upgraded, all of which lead to repeat purchases. We will model repeat purchase behavior by assuming that adopters move back into the population of potential adopters when their first unit is discarded or consumed.
First, we will define a constant representing the average life time of product.
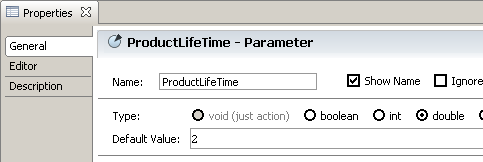
![]() Create the ProductLifeTime constant
Create the ProductLifeTime constant
- Assume that the average duration of active use of our product is 2 years. Type 2 as the Default Value.
People move back from the adopter population to the pool of potential adopters when the product they have purchased is discarded or consumed. So, the discard flow is nothing else but the adoption flow delayed on the average life time of the product.
![]() Create the discard flow Adopters to PotentialAdopters
Create the discard flow Adopters to PotentialAdopters
- First, double-click Adopters stock in the graphical editor.
- Then click PotentialAdopters variable.
- New flow from Adopters to PotentialAdopters is added. Change the name of the flow to DiscardRate (do not forget to press Ctrl+Enter when finished typing new flow name).
- You can see that stock formulas have changed as well:


- Set the following formula for the flow variable:
delay(AdoptionRate, ProductLifeTime)
The delay() function implements the time delay and has the following notation:delay(<variable>, <delay value>, <initial value>)
In our case, function reproduces AdoptionRate delayed on the ProductLifeTime value. The discard rate is null until the time of use of the first purchased products elapses.
Now we have finished modeling the product replacement purchases. You may check how the delay function works. Run the model and view plots for AdoptionRate and DiscardRate. You can see that rate curves look exactly how we expected — the discard rate is actually the adoption rate delayed by 2 years — the life time of the product.
Observe the population dynamics using the chart. Now, instead of falling to zero, the potential adopter population is constantly replenished as adopters discard the product and reenter the market. The adoption rate rises, peaks, and falls to a rate that depends on the average life of the product and the parameters determining the adoption rate. Discards mean there is always some fraction of the population in the potential adopter pool.
If you like, you may add control group varying product life time, say from 0.5 to 10.



