Signals and Systems/Z-Transform Introduction
Sampled Systems
[edit | edit source]Digital signals are by essence sampled signals. In a circuit node, the numbers change at a given rate: the sampling rate or sampling frequency. The time between two changes of the signal is the inverse of the sampling frequency: it is the sampling period.
In processor systems, samples are stored in memory. In logic circuits, they correspond to register outputs. The sampling period is used to compute the next value of all signals in the system.
Digital circuits are not the only sampled systems: analog circuits such as switched capacitor filters also rely on switches and are sampled too.
Sampling a signal
[edit | edit source]The Nyquist Rate
[edit | edit source]Sampling a signal raises a major question: does one lose information during this process?

On the other side, sampling the traffic lights once per microsecond doesn't bring much more information than sampling it every millisecond.
Obviously, the traffic lights, as any other signals, have to be sampled at a faster rate than they change, but sampling them very much faster doesn't bring more information.
The Nyquist rate is the minimum sampling rate required to avoid loss of information.
where is the highest frequency of the signal to be sampled, also called bandwidth.
To avoid losing information, the sampling rate must be higher than the Nyquist rate:
In practice, the sampling rate is taken with some margin, in order to more easily reconstruct the original signal.

The full range of human hearing is between 20 Hz and 20 kHz. Thus, audio content has to be sampled at more than 40 kHz.
And indeed:
- CD audio samples the signals at 44.1 kHz.
- Professional digital video equipment samples them at 48 kHz.
- DVD audio samples them at 96 kHz.
- High end DVD audio doubles this frequency to 192 kHz.
Aliasing
[edit | edit source]Sampling a signal with a rate lower than the Nyquist Rate produces aliasing or folding.
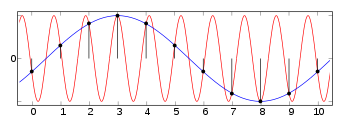
The picture on the right shows a red sinewave of frequency 0.9 (and thus of a period close to 1.1). This signal should be sampled with a frequency larger than 1.8. However, the signal has been sampled with a rate of 1 (vertical lines and black dots). If one tries to draw a line between the samples, the result will look like the blue curve which is a sinewave of period 10, or of frequency 0.1.
If the signal would have been sampled at a rate of 0.9, the sampling points would always fall on the same point in the sine function and the resulting signal would seem to be a constant.
Sampling a signal of frequency 0.9 with a rate of 1 creates an alias with the frequency of .
Sampling a signal of frequency 0.9 with a rate of 0.9 creates an alias at DC, and so with the frequency of .
Sampling a signal of frequency 0.9 with a rate of 0.8 also creates an alias with the frequency of , but with a different phase.

Illuminating a motor turning at a frequency of 90 Hz with a stroboscope switching at 100 Hz gives us the impression that is it turning at 100 Hz - 90 Hz = 10 Hz.
Illuminating a motor turning at a frequency of 90 Hz with a stroboscope switching at 90 Hz gives us the impression that is it standing still.
Illuminating a motor turning at a frequency of 90 Hz with a stroboscope switching at 80 Hz gives us the impression that is it turning at 90 Hz - 80 Hz = 10 Hz, but in the opposite direction.
This is the same effect seen in many American Western movies containing stagecoach scenes. At various rotational rates, the wheels on the stagecoach will appear to rotate forward, stand still, or rotate backward. See Wagon-wheel effect.
It is as if the spectrum of the signal has been folded back down at a point equal to half the sampling frequency.
Undersampling
[edit | edit source]Sampling a frequency lower than the Nyquist rate, also called undersampling, creates sinewave aliases at a lower frequency. If the original signal also has content at these lower frequencies, then they will be mixed and there is a loss of information.
However, if the signal has only high-frequency content, then the undersampling process modulates the signal at a lower frequency.
This is a cheap alternative to modulating by the multiplication with a modulation sinewave.
Oversampling
[edit | edit source]Oversampling corresponds to sampling with a frequency much higher (typically 100 to 1000) than the Nyquist rate. The interest of oversampling is to be able to represent the signal with a smaller amount of bits.
This can be explained by the mechanism used to gain the additional bits back: a signal sampled at 10 kHz can be downsampled at 5 kHz as long as the new sampling frequency remains greater than the Nyquist frequency. The downsampling implies having two times fewer samples. Rather than throwing every second sample away, one can calculate the mean value of two consecutive samples and use this result to build one sample of the new signal. Calculating the mean value corresponds to add the values and divide them by two. Rather than dividing the result by two and throwing away the bit after the decimal point, one can only add the consecutive samples two by two. With this, the amplitude of the 5 kHz signal is twice the one of the original 10 kHz signal. In other words, it has to be represented by 1 more bits.
A largely used application of oversampling is Pulse Width Modulation (PWM). The modulated signal is represented with a single bit switching at a frequency equal to , where is the Nyquist frequency of the original signal and the number of bits with which it is represented. This one bit signal is ideal to drive high-current loads with a single power switch. PWM is typically used for driving electric motors.
A more complex coding scheme for a result on a single bit is found in every CD player: sigma-delta modulation. There is more theory required for understanding its working. Let us state that it is able to represent a signal on a single bit at a lower sampling frequency than the PWM. On the other hand, the one bit signal switches back and forth more frequently at its sampling frequency and is thus less indicated for driving slower high-current switches. Sigma-delta modulation is used for driving lighter loads such as the cable between the CD player and the audio amplifier.

The SACD codes the audio in the form of a Direct Stream Digital signal coded on a single bit at 64 times the CD sampling rate of 44.1 kHz.
Z Transform
[edit | edit source]The Z Transform is used to represent sampled signals and Linear Time Invariant (LTI) systems, such as filters, in a way similar to the Laplace transform representing continuous-time signals.
Signal representation
[edit | edit source]The Z Transform is used to represent sampled signals in a way similar to the Laplace transform representing continuous-time signals.
A sampled signal is given by the sum of its samples, each one delayed by a different multiple of the sampling period. The Laplace transform represents a delay of one sampling period by:
With this, the Z-transform can be represented as
where the are the consecutive values of the sampled signal.
Linear time invariant systems
[edit | edit source]Continuous-time Linear Time Invariant (LTI) systems can be represented by a transfer function which is a fraction of two polynomials of the complex variable .
Their frequency response is estimated by taking , this is by estimating the transfer function along the imaginary axis.
In order to ensure stability, the poles of the transfer function (the roots of the denominator polynomial) must be on the left half plane of .

Discrete-time LTI systems can be represented by the fraction of two polynomials of the complex variable :
From the definition:
we find that their frequency response can be estimated by taking , this is by estimating the transfer function around the unit circle.
In order to ensure stability, the poles of the transfer function (the roots of the denominator polynomial) must be inside the unit circle.
Transfer function periodicity
[edit | edit source]The transfer function is estimated around the unit circle:
- The point at coordinate corresponds to frequency , which is DC.
- The point at coordinate corresponds to frequency , the quarter of the sampling frequency.
- The point at coordinate corresponds to frequency , half the sampling frequency.
- The point at coordinate corresponds to frequency .
- The point at coordinate corresponds to frequency which is the sampling frequency.
So having turned once around the unit circle, one falls back to the starting point . From there, one can make another turn from to , and one more from to and so on... On each of these turns, the frequency response will be the same. In other words, the transfer function of a sampled system is periodic of period equal to the sampling frequency.
With real (as opposed to complex) signals, the transfer function is symmetric around half the sampling frequency: . So the transfer function of a sampled system is usually only considered between and .











![{\displaystyle X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n=0}^{\infty }x[n]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002b8402b1078b72fcc49efe3b0c15d275cd9ad4)
![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)


















