Signal Processing/Analog Filters
Analog Filters
[edit | edit source]Historically, electric signal processing started with analog circuits. Signal analysis and filter design methods first based on these kind of circuits. Later came the avent of digital systems. The first digital filters relied on the techniques used for their analog parents. Still today, some digital filters rely on the simulation of analog filters in order to profit from some of their interesting properties.
Passive Filters
[edit | edit source]Lumped Elements Filters
[edit | edit source]Lumped elements filters base on the frequency characteristics of the following components:
- the resistance, R
- the capacitance, C
- the inductance, L
Their characteristics are given by:
Ladder filters
[edit | edit source]The following image shows a 4th order all-pole lowpass ladder filter:

The overall appearance of the circuit explains the name.
In the drawing, the source and load resistance are identical. This corresponds to the situation with the best energy transfer from source to load. At DC, the inductances act as short circuits and the capacitances as open circuits. Hence the output amplitude will be half of the one of the input.
Doubly terminated ladder filters show to have excellent passband sensitivity properties [1]. In other terms, a given change in L or C element values results in a much smaller relative change in the filter transfer function. Because of this, ladder filters have been widely used as a model for analog active filters and for digital filters.
Filters with Distributed Elements
[edit | edit source]A distributed element filter is an electronic filter in which capacitances, inductances and resistances (the elements of the circuit) are not localised in discrete (lumped) elements as they are in conventional filters. At high frequencies, in the microwave region, the strips on a printed circuit board act as impedances and a careful design of them allows to implement filter functions.
Active Filters
[edit | edit source]Active filters are analog filters using amplifying devices such as operational amplifiers. They allow to realize filter functions with resistances and capacitances, freing the designer of the need to use inductances.
Canonical filters
[edit | edit source]The first attempts to realize active filters was to devise a circuit realizing the transfer function, with R and C element value combinations corresponding to the transfer function's numerator and denominator coefficients: the canonical filters. However, this kind of circuits showed to be very sensitive to element values: a small change in an R or C element value had a large effect on the transfer function.
For that reason, the design of active filters has shifted from canonical filters to other structures such as chains of second order sections or leapfrog filters.
Chain of Second Order Sections
[edit | edit source]A second order section, often referred as biquad, implements a second order transfer function. The transfer function of a filter can be split into a product of transfer functions each associated to a pair of poles and possibly a pair of zeroes.
The transfer function of a system given with an equal number of complex conjugate zeroes, and , and poles and , together with a gain is:
This is the case for Chebyshev type 2 and Elliptic filter functions.
Writing:
shows that the denominator polynomial functions of have real coefficients. The same can be said for the numerator. With this, the transfer function can be rewritten as:
If the transfer function's order is odd, then a first order section has to be added to the chain. This section is associated to the real pole and to the real zero , if there is one. The transfer function becomes:
An all-pole even order transfer function is in the form:
This is the case for Butterworth, Chebyshev type 1 and Bessel filter functions.
An all-pole odd order transfer function is in the form:
State Variable Filters
[edit | edit source]State Variable Filters have a topology with two integrators whose outputs correspond to the state-space variables associated with the transfer funtion.
The following circuit was proposed by Kerwin, Huelsman and Newcomb [2]:
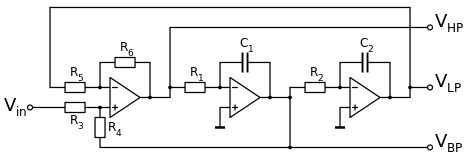
The following circuit is know as the Tow-Thomas circuit [3]:

It is possible with both the Kerwin-Huelsman-Newcomb and the Tow-Thomas to build a weighted sum of all op-amp outputs in order to obtain a more generic transfer function.
Certain second order canonical structures directly use the transfer function's coefficients as amplifier gains.
Sallen and Key circuits
[edit | edit source]The Sallen–Key topology uses an operational amplifier to drive the output and R C elements to set the transfer function. Due to the driving capacity of operational amplifiers, Sallen–Key circuits are easily cascaded to form a higher order filters.
The following circuits shows a Sallen–Key lowpass filter circuit:

Leapfrog Filters
[edit | edit source]Filter Structure
[edit | edit source]Leapfrog filters are based on the simulation of passive ladder filters. The incentive for this choice is to inherit from the excellent passband sensitivity properties of the original circuit.
Taking the example of the following 4th order all-pole lowpass ladder filter,

one can write the following equations:
Rewriting these equations gives:
This new set of equations shows that the filter can be implemented with a chain of 4 integrators with:
- state variables having the form of or
- time constants having the form of or
The resulting circuit is an integrator chain where each integrator output is brought back to the preceeding integrator input. Hence the name Leapfrog.

Transfer Function
[edit | edit source]The set of equations describing the filter can be rewritten using the state space representation as:
From this equation set, one can write the A, B, C, D matrices as:
From this representation, signal processing tools such as Octave or Matlab allow to plot the filter's frequency response or to examine its zeroes and poles.
Switched-Capacitor Filters
[edit | edit source]Switched-capacitor filters are analog sampled devices. Charging and discharging a capacitor can show to produce an impedance close to the one of a resistance. With this, RC time constants of an analog active filter are changed into a factor proportional to the ratio of two capacitances. This kind of circuit is most interesting for integrated circuit design, where R and C element values can largely vary from one die to another, whilst the ratio of two capacitances in the same region of a silicon device remains very precise.
References
[edit | edit source]- ↑ Johns David A.; et al. (1989). "Orthonormal Ladder Filters" (PDF). IEEE Transactions on Circuits and Systems. New York, IEEE Circuits and Systems Society. 36 (3): 337–343.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ↑ Kerwin, W.J. Huelsman, L.P. Newcomb, R.W. (1967). "State-Variable Synthesis for Insensitive Integrated Circuit Transfer Functions". IEEE Journal of Solid-State Circuits. 2 (3): 87–92.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Lee C. Thomas (1971). "The Biquad: Part I-Some practical design considerations". IEEE Transactions on Circuit Theory. 18 (3): 350–357.




























