Probability/Set Theory

Introduction

The overview of set theory contained herein adopts a naive point of view. A rigorous analysis of the concept belongs to the foundations of mathematics and mathematical logic. Although we shall not initiate a study of these fields, the rules we follow in dealing with sets are derived from them.

Sets

Definition. (Set) A set is a well-defined collection of distinct object(s), which are called element(s).

A set.

Remark.

• If $x$ belongs to (or is contained in) a set $S$ , we write $x\in S$.
• If $x$ does not belong to the set $S$ , we write $x\notin S$.
• When $x$ and $y$ are equal, denoted by $x=y$, $x$ and $y$ are different symbols denoting the same object(s). (When $x$ and $y$ are not equal, we write $x\ne y$, and they are different things.)
• Because of the vagueness of the term "well-defined", some may not accept this "definition" as a definition of set. Sometimes, a set may be left as a primitive notion, i.e., an undefined term.

Example. (Collection that is not "well-defined")

• The collection of easy school subjects is not a set, since "easy" is not well-defined.

We have different ways to describe a set, e.g.

• word description: e.g., a set $S$ is the set containing the 12 months in a year;
• listing: elements in a set are listed within a pair of braces, e.g., $S\stackrel{\text{ def }}{=}\{\text{January, }\text{March, February, }\text{April, May, June, July, August, September, October, November, December}\}$;

the ordering of the elements is not important, i.e. even if the elements are listed in different order, the set is still the same. E.g., $\{\text{January, }\text{February, March, }\text{April, May, June, July, August, September, October, November, December}\}$ is still referring to the same set.

• set-builder notation:$$\underset{\text{The set of}}{\underbrace{\{}}\underset{\text{all elements }x}{\underbrace{x}}\underset{\text{such that }}{\underbrace{:}}\underset{\text{the property }P(x)\text{ holds}}{\underbrace{P(x)}}\}$$

(the closing brace must also be written.)

For example, $S\stackrel{\text{ def }}{=}\{x:x\text{ is a month in a year}\}$.

Example. (Empty set) The set $\{\}$ is called an empty set, and it contains no element. It is commonly denoted by $\varnothing$ also.

Exercise.

Is $\{\varnothing \}$ an empty set?

	Yes.
	No.

Example.

• $\text{apple}\in \{\text{apple, orange, banana}\}$;
• $\varnothing \in \{\varnothing \}$;
• $\varnothing \notin \varnothing$.

Exercise.

Select all element(s) belonging to the set $\{\varnothing ,\{\varnothing \},\{\{\varnothing \}\}\}$.

	$\varnothing$
	$\{\varnothing \}$
	$\{\varnothing ,\{\varnothing \}\}$
	$\{\{\varnothing \}\}$
	$\{\{\varnothing ,\{\varnothing \}\}\}$

Example.

• Let $S_1$ be the set containing all outcomes from rolling a six-faced dice. Then, we can express the set $S_1$ as $\{1,2,3,4,5,6\}$.
• Let $S_2$ be the set containing all outcomes from tossing a coin. Then, we can express the set $S_2$ as $\{H,T\}$ where $H$ stands for "heads" and $T$ stands for "tails".

Exercise. Amy participates in a lucky draw where the grand prize is a car. Suppose we say that the outcome is 1 if Amy gets the grand prize, and 0 otherwise, what is the set containing all outcomes?

Solution

The set is $\{0,1\}$.

Definition. (Set equality) When two sets are equal, they contain the same elements.

Remark.

• Equivalently, two sets $A$ and $B$ are equal if each element of $A$ is also element of $B$ and each element of $B$ is also element of $A$.
• We use $A=B$ to denote sets $A$ and $B$ are equal ($A\ne B$ is used to denote $A$ and $B$ are not equal).

Example.

• $\{\varnothing \}=\{x:x\text{ is a empty set}\}$.
• $\varnothing =\{\}\ne \{\{\}\}=\{\varnothing \}$.
• $\{2,3,5\}=\{x:x\text{ is a prime number that is not greater than }5\}$

Example. Let $S_1$ be the set containing all odd outcomes from rolling a six-faced dice. Also, let $S_2$ be the set containing all outcomes that are not even from rolling a six-faced dice. Then, $S_1=S_2=\{1,3,5\}$.

Definition. (Universal set) Universal set, denoted by $U$, is the set that contains all objects being considered in a particular context.

Remark.

• In the context of probability, a universal set, which is usually denoted by $\mathrm{\Omega }$ instead, is the set containing all outcomes of a particular random experiment, and is also called a sample space.

Example. The sample space of rolling a six-faced dice is $\mathrm{\Omega }=\{1,2,3,4,5,6\}$.

Exercise. What is the sample space of tossing a coin? (Use $H$ to stand for the outcome "heads" and $T$ to stand for the outcome "tails".)

Solution

The sample space is $\mathrm{\Omega }=\{H,T\}$.

Definition. (Cardinality) Cardinality of a finite set is the number of its elements.

Remark.

• A set is said to be finite if it is empty set or it contains $n\in \mathbb{N}$ elements ($\mathbb{N}$ is the set containing all positive integers).
• Cardinality of set $S$ can be denoted by $\mathrm{\#}(S)$ (or $|S|$).
• Infinite set is a set containing infinite number of elements.

• We will leave the cardinality of infinite set undefined in this book, but it can be defined, in a more complicated way.

Example.

• $\mathrm{\#}(\{\{1\},2,3\})=3$.
• $\mathrm{\#}(\varnothing )=0$.
• $\mathbb{N}$ (the set containing each positive integer) is an infinite set.

Exercise.

Calculate $\mathrm{\#}(\{\varnothing ,\{\varnothing \}\})$.

	0
	1
	2
	3
	None of the above.

Example. Let $\mathrm{\Omega }$ be the sample space of rolling a six-faced dice and $S$ be the set containing all odd outcomes from rolling a six-faced dice. Then, $\mathrm{\#}(S)=3$ and $\mathrm{\#}(\mathrm{\Omega })=6$.

Exercise. A student is asked to show that two sets $A$ and $B$ are equal in a question of his assignment. In that question, one of the given condition is that $\mathrm{\#}(A)=\mathrm{\#}(B)$. The student then makes the following argument:

Since $\mathrm{\#}(A)=\mathrm{\#}(B)$, it follows that $A=B$.

Is his argument correct? If not, provides an example of sets $A$ and $B$ such that $\mathrm{\#}(A)=\mathrm{\#}(B)$ but $A\ne B$.

Solution

The argument is wrong. We can take, for example, $A=\{1\}$ and $B=\{2\}$. Then, $\mathrm{\#}(A)=\mathrm{\#}(B)=1$ but $\{1\}\ne \{2\}$.

Subsets

We introduce a relationship between sets in this section.

Definition. (Subset) $A$ is a subset of $B$, denoted by $A\subseteq B$ if each element of set $A$ is an element of set $B$.

Remark.

• If $A$ is not a subset of $B$, then we write $A\subseteq ̸B$.
• By referring to the definitions of subsets and set equality, we can see that $A=B$ is equivalent to (or if and only if) $A\subseteq B$ and $B\subseteq A$.
• The notation $A\supseteq B$ means that $A$ is a superset of $B$, which means that $B$ is a subset of $A$.

• This notation and terminology are seldom used.

Definition. (Venn diagram) A Venn diagram is a diagram that shows all possible logical relations between finitely many sets.

Remark.

• It is quite useful for illustrating some simple relationships between sets, and making the relationships clear.
• We may also add various annotations in the Venn digram, e.g. cardinality of each set, and the element(s) contained by each set.

Illustration of subset by Venn diagram:

A ⊆ B (A ≠ B):

*-----------------------*
|                       |
|                       |
|   *----------*        | <---- B
|   |          |        |
|   |    A     |        |
|   |          |        |
|   *----------*        |
*-----------------------*

Example.

• $\{1,3\}\subseteq \{1,2,3\}$.

Venn digram:

*--------------------*
|   *----------*  2  | 
|   |    1  3  |     |
|   *----------*     |
*--------------------*

• $\{\{1\}\}\subseteq ̸\{1,2,3\}$ ($\{1\}\notin \{1,2,3\}$).
• It can be proved that $\varnothing \subseteq S$ for each set $S$.

Example. Let $\mathrm{\Omega }$ be the sample space of rolling a six-faced dice and $S$ be the set containing all odd outcomes from rolling a six-faced dice. Then, $S\subseteq \mathrm{\Omega }$.

Exercise. Let $P$ be the set containing all prime outcomes from rolling a six-faced dice. Is $P$ a subset of $S$?

Solution

No, since $2\in P$ but $2\notin S$.

Example. (Intervals) Intervals are commonly encountered subsets of $ℝ$. If $a$ and $b$ are real numbers such that $a<b$, then $$\begin{array}{cc}(a,b)& \stackrel{\text{ def }}{=}\{x\in ℝ:a<x<b\};\\ [a,b)& \stackrel{\text{ def }}{=}\{x\in ℝ:a\le x<b\};\\ (a,b]& \stackrel{\text{ def }}{=}\{x\in ℝ:a<x\le b\};\\ [a,b]& \stackrel{\text{ def }}{=}\{x\in ℝ:a\le x\le b\}.\\ \end{array}$$ In particular, $(-\mathrm{\infty },\mathrm{\infty })=ℝ$.

We also have $[-\mathrm{\infty },\mathrm{\infty }]$, which is the set containing all extended real numbers, i.e., $[-\mathrm{\infty },\mathrm{\infty }]=(-\mathrm{\infty },\mathrm{\infty })\cup \{-\mathrm{\infty },\mathrm{\infty }\}$. Such notation is occasionally used. (Extended real number system is obtained by adding $\mathrm{\infty }$ and $-\mathrm{\infty }$ to the real number system.)

Definition. (Proper subset) A set $A$ is a proper subset of set $B$ if $A\subseteq B$ and $A\ne B$;. We write $A⊊B$ in this case.

Remark.

• If a set $A$ is not a proper subset of $B$, then we write $A⊊̸B$ (but we rarely write this).
• The notation $A⊋B$ means that $A$ is a proper superset of $B$, which means that $B$ is a proper subset of $A$.

• This notation and terminology are seldom used.

Example.

• The set $\{1,2\}$ is not a proper subset of itself, i.e., $\{1,2\}⊊̸\{1,2\}$.
• $\{1\}⊊\{1,2\}$.

Definition. (Complement) Let $A$ be a subset of universal set $U$. The (absolute) complement of $A$, denoted by $A^c$, is the set $\{x\in U:x\notin A\}$.

Example. If $A=\{1,2,3\}$ and $U=\{1,2,3,4,5\}$, then $A^c=\{4,5\}$.

Venn diagram:

*-----------------------*
|                       |
|    A           4  5   |
|   *----------*        | 
|   |          |        | <---- U
|   |  1 2  3  |        |
|   |          |        |
|   *----------*        |
*-----------------------*

Exercise.

Find ${\varnothing }^c$.

	$U$
	$\{U\}$
	$\varnothing$
	$\{\varnothing \}$
	None of the above.

Set operations

Probability theory makes extensive use of some set operations, and we will discuss them in this section.

Definition. (Union of sets) The union of set $A$ and set $B$, denoted by $A\cup B$, is the set $\{x:x\in A\text{ or }x\in B\}$.

Union of two sets is indicated by the red region.

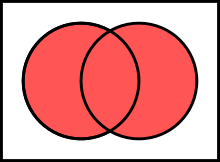
Remark.

• $A\cup B$ is read 'A cup B'.

Example.

• $\{\text{apple},\text{orange}\}\cup \{\text{orange},\text{red}\}=\{\text{apple},\text{orange},\text{red}\}$.

Venn diagram:

*----------------*
|                |
|  red   *-------*--------*
|        | orange|        |
*--------*-------*        |
         |       apple    |
         *----------------*

In the following, some basic properties possessed by the union operation: commutative law and associative law, are introduced.

Proposition. (Properties of union of sets) Let $A,B$ and $C$ be sets. Then, we have

(a) $A\cup B=B\cup A$ (commutative law);

(b) $A\cup (B\cup C)=(A\cup B)\cup C$ (associative law).

Remark.

• Because of the associative law, we can write the union of three or more sets without ambiguity. For instance, we can write $A\cup B\cup C$ directly, since $A\cup (B\cup C)=(A\cup B)\cup C$.

Example. Let $A_1=\{1,2\},A_2=\{3,4,5\}$ and $A_3=\{6,7\}$. Then,

• $\bigcup _{i=1}^3{A}_i=A_1\cup A_2\cup A_3=\{1,2,3,4,5,6,7\}$
• $\bigcup _{i=2}^3{A}_i=A_2\cup A_3=\{3,4,5,6,7\}$
• $A_1\cup A_3=\{1,2,6,7\}$.

($\bigcup _{i=m}^n{A}_i$ means $A_m\cup A_{m+1}\cup \cdots \cup A_n$ ($n>m$), and $\bigcup _{i=m}^{\mathrm{\infty }}{A}_i$ means $A_m\cup A_{m+1}\cup \cdots$.)

Definition. (Intersection of sets) The intersection of set $A$ and set $B$, denoted by $A\cap B$, is the set $\{x:x\in A\text{ and }x\in B\}$.

Intersection of two sets.

Remark.

• $A\cap B$ is read 'A cap B'.

Example.

• $\{1,2,3\}\cap \{2,3,4\}=\{2,3\}$.
• $\{1,2,3\}\cap \{4,5,6\}=\varnothing$.

Definition. (Disjoint sets) Sets $A$ and $B$ are disjoint (or mutually exclusive) if $A\cap B=\varnothing$.

Example. The sets $\{1,2,3\}$ and $\{4,5,6\}$ are disjoint.

Remark.

• I.e., $A$ and $B$ are disjoint if they have no element in common.
• More than two sets are said to be disjoint if they are pairwise disjoint.

Venn diagram

*-----*       *-----*       *-----*       
|     |       |     |       |     |
|  A  |       |  B  |       |  C  |
*-----*       *-----*       *-----*

(A, B and C are disjoint)
      
*----------------*
|                | <---- D 
| *--*   *-------*--------*               
| |  |   |       |        | 
*-*--*---*-------*        | <--- E
  |  |   |                |
  *--*   *----------------*
   ^
   |
   F

(D, E and F are not disjoint, but E and F are disjoint)

Proposition. (Properties of intersection of sets) Let $A$,$B$ and $C$ be sets. Then, we have

(a) $A\cap B=B\cap A$ (commutative law);

(b) $A\cap (B\cap C)=(A\cap B)\cap C$ (associative law);

Remark.

• Likewise, we denote $A_m\cap A_{m+1}\cap \cdots \cap A_n$ by $\bigcap _{i=m}^n{A}_i$ ($n>m$).
• Also, we denote $A_m\cap A_{m+1}\cap \cdots$ (never ends) by $\bigcap _{i=m}^{\mathrm{\infty }}{A}_i$.
• For (a), the equation can be interpreted as "distributing" $A\cup$ into the bracket.
• For (b), the equation can be interpreted as "distributing" $A\cap$ into the bracket.

Example. For every positive integer $j$, defines $A_j=\{n\in \mathbb{N}:n\ge j\}$. Then, $$\bigcap _{i=1}^{10}{A}_i=\{1,2,3,\dots \}\cap \{2,3,4,\dots \}\cap \cdots \cap \{10,11,12,\dots \}=\{10,11,12,\dots \}=\{n\in \mathbb{N}:n\ge 10\}=A_{10}.$$

The following result combines the union operation and intersection operation.

Proposition. (Distributive law) Let $A$,$B$ and $C$ be sets. Then, the following statements hold.

(a) $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$;

(b) $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$.

Example. Let $A=\{1,2,3\},B=\{2,3,4\}$ and $C=\{1,5,6\}$. Verify that the distributive law (a) holds for these three sets, i.e., show that $$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$$ for these three sets $A,B,C$.

Solution. First, $A\cap (B\cup C)=A\cap \{1,2,3,4,5,6\}=\{1,2,3\}$. On the other hand, $(A\cap B)\cup (A\cap C)=\{2,3\}\cup \{1\}=\{1,2,3\}$.

Exercise. Verify that the distributive law (b) holds for these three sets.

Solution

First, $A\cup (B\cap C)=A\cup \varnothing =A=\{1,2,3\}$. On the other hand, $(A\cup B)\cap (A\cup C)=\{1,2,3,4\}\cap \{1,2,3,5,6\}=\{1,2,3\}$.

Definition. (Relative complement) The relative complement of set $A$ in set $B$, denoted by $B\setminus A$, is the set $\{x:x\in B\text{ and }x\notin A\}$.

The relative complement of $A$ (left) in $B$ (right) ($B\setminus A$), given by the red region.

Remark.

• If $U$ is the universal set and $A$ is a subset of $U$, then $A^c=U\setminus A$.
• $B\setminus A$ is read 'B take away A'.

Example.

• $\{1,2,3\}\setminus \{1,2\}=\{3\}$;
• $\{1,2,3\}\setminus \{1,2,3\}=\varnothing$;
• $\{1,2,3\}\setminus \{4,5,6\}=\{1,2,3\}$.

Theorem. (De Morgan's laws) Let $B,A_1,A_2,\dots$ be sets. Then, $$B\setminus (A_1\cup A_2\cup \cdots )=(B\setminus A_1)\cap (B\setminus A_2)\cap \cdots \text{ and }B\setminus (A_1\cap A_2\cap \cdots )=(B\setminus A_1)\cup (B\setminus A_2)\cup \cdots$$

Remark.

• Special case: If $B=U$, then the equations become $(A_1\cup A_2\cup \cdots {)}^c=A_1^c\cap A_2^c\cap \cdots \text{ and }(A_1\cap A_2\cap \cdots {)}^c=A_1^c\cup A_2^c\cup \cdots$.

Example. Let $A=\{1,2,3\},B=\{1,3\},C=\{1,2,3,4\}$, and let the universal set be $U=\{1,2,3,4,5\}$. For these three sets $A,B,C$,

(a) Verify that $A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$.

(b) Verify that $C\setminus (A\cup B)=(C\setminus A)\cup (C\setminus B)$.

Solution.

(a) First, $A\setminus (B\cup C)=A\setminus \{1,2,3,4\}=\varnothing$. On the other hand, $(A\setminus B)\cap (A\setminus C)=\{2\}\cap \varnothing =\varnothing$. So, we have the desired equality.

(b) First, $C\setminus (A\cup B)=C\setminus \{1,2,3\}=\{4\}$. On the other hand, $(C\setminus A)\cup (C\setminus B)=\{4\}\cap \{2,4\}=\{4\}$.

Exercise. Verify that $(A\cup B\cup C{)}^c=A^c\cap B^c\cap C^c$ for these three sets $A,B,C$.

Solution

First, $(A\cup B\cup C{)}^c=(\{1,2,3,4\}{)}^c=\{5\}$. On the other hand, $A^c\cap B^c\cap C^c=\{4,5\}\cap \{2,4,5\}\cap \{5\}=\{5\}$.

Definition. (Power set) The power set of a set $A$, denoted by $𝒫(A)$, is the set of all subsets of $A$, i.e., $\{S:S\subseteq A\}$.

Example.

• $𝒫(\{1,2\})=\{\varnothing ,\{1\},\{2\},\{1,2\}\}$;
• $𝒫(\varnothing )=\{\varnothing \}$ (power set of an empty set is not an empty set).

Remark.

• Power set of a set containing $n$ elements contains $2^n$ elements.

• See the chapter about combinatorics for a proof of this statement.

Example. Let $\mathrm{\Omega }=\{H,T\}$ be the sample space of tossing a coin ($H$ and $T$ stand for "heads" and "tails" respectively). Then, $$𝒫(\mathrm{\Omega })=\{\varnothing ,\{H\},\{T\},\{H,T\}\}.$$

Exercise. Suppose we toss a coin twice. Then, the sample space of this random experiment is $$\mathrm{\Omega }=\{HH,HT,TH,TT\}$$ where $HH$ means "heads" followed by "heads", $HT$ means "heads" followed by "tails", etc. Notice that the order matters, and hence $HT$ is different from $TH$.

(a) Find the power set $𝒫(\mathrm{\Omega })$. (Suggestion: check whether your power set contains $2^4=16$ elements.)

(b) Define the set $S$ to be the set containing subsets of $\mathrm{\Omega }$ that includes the outcome $HH$. That is, $S=\{X\subseteq \mathrm{\Omega }:HH\in X\}$. Find $\mathrm{\#}(S)$.

Solution

(a) The power set is $$\begin{array}{cc}𝒫(\mathrm{\Omega })=\{& \varnothing ,\{HH\},\{HT\},\{TH\},\{TT\},\\ & \{HH,HT\},\{HH,TH\},\{HH,TT\},\{HT,TH\},\{HT,TT\},\{TH,TT\},\\ & \{HH,HT,TH\},\{HH,HT,TT\},\{HH,TH,TT\},\{HT,TH,TT\},\{HH,HT,TH,TT\}\}\end{array}$$ (b) By observing the power set in (a), we can see that 8 subsets (green one) of $\mathrm{\Omega }$ contains the outcome $HH$. So, $\mathrm{\#}(S)=8$.

Definition. ($n$-ary Cartesian product) The $n$-ary Cartesian product over $n$ sets $S_1,\dots ,S_n$, denoted by $S_1\times \cdots \times S_n$, is $$\{(s_1,\dots ,s_n):s_i\in S_i\text{ for each }i\in \{1,\dots ,n\}\}.$$

Remark.

• It can be proved that $\mathrm{\#}(S_1\times \cdots \times S_n)=\mathrm{\#}(S_1)\times \cdots \times \mathrm{\#}(S_n)$.
• $(s_1,\dots ,s_n)$ is ordered, i.e., the order matters for the things inside it.
• When $n=2$, $(s_1,s_2)$ is called an ordered pair.
• It is common to use ${ℝ}^n$ to denote $\underset{n\text{ times}}{\underbrace{ℝ\times ℝ\times \cdots \times ℝ}}$.

Example. Let $A=\{1,2\},B=\{2,3\}$ and $C=\{3,4\}$. Then,

• $A\times B=\{(1,2),(1,3),(2,2),(2,3)\}$.
• $B\times C=\{(2,3),(2,4),(3,3),(3,4)\}$.
• $A\times B\times C=\{(1,2,3),(1,2,4),(1,3,3),(1,3,4),(2,2,3),(2,2,4),(2,3,3),(2,3,4)\}$.

Exercise. A restaurant offers a set lunch where the customer can choose one food/drink from each of group A,B,C:

• group A: egg, beacon
• group B: steak, salmon
• group C: tea, milk, water

We define the sets $A,B,C$, corresponding to these three groups A,B,C:

• $A=\{\text{egg},\text{beacon}\}$
• $B=\{\text{steak},\text{salmon}\}$
• $C=\{\text{tea},\text{milk},\text{water}\}$

(a) Find the set $A\times B\times C$, which contains every possible combination of choices made by the customer.

(b) Suppose the tea in the restaurant is out of stock, so the customer cannot choose tea in group C now. Suppose the set $A\times B\times C^{\ast }$ now contains every possible combination of choices made by the customer. What should be the set $C^{\ast }$? What is the cardinality of the set $A\times B\times C^{\ast }$?

Solution

(a) The set $A\times B\times C$ is given by $$\begin{array}{cc}A\times B\times C=\{& (\text{egg},\text{steak},\text{tea}),(\text{egg},\text{steak},\text{milk}),(\text{egg},\text{steak},\text{water}),\\ & (\text{egg},\text{salmon},\text{tea}),(\text{egg},\text{salmon},\text{milk}),(\text{egg},\text{salmon},\text{water}),\\ & (\text{beacon},\text{steak},\text{tea}),(\text{beacon},\text{steak},\text{milk}),(\text{beacon},\text{steak},\text{water}),\\ & (\text{beacon},\text{salmon},\text{tea}),(\text{beacon},\text{salmon},\text{milk}),(\text{beacon},\text{salmon},\text{water})\}\end{array}$$ (b) The set $C^{\ast }$ should be $\{\text{milk},\text{water}\}$. The cardinality of the set $A\times B\times C^{\ast }$ is $2\times 2\times 2=8$.