Principles of Biochemistry/Water: The solvent of the cell
Water is a chemical substance with the chemical formula H2O. Its molecule contains one oxygen and two hydrogen atoms connected by covalent bonds.

Water on Earth
[edit | edit source]Water is widely distributed on Earth as freshwater and saltwater. The Earth is often referred to as the "blue planet" because when viewed from space it appears blue. This blue color is caused by reflection from the oceans which cover roughly 70% of the area of the Earth. The oceanic crust is young, thin and dense, with none of the rocks within it dating from any older than the breakup of Pangaea. Because water is much denser than any gas, this means that water will flow into the "depressions" formed as a result of the high density of oceanic crust. On a planet like Venus, with no water, the depressions appear to form a vast plain above which rise plateaus.
Saltwater
[edit | edit source]
Since the low density rocks of the continental crust contain large quantities of easily eroded salts of the alkali and alkaline earth metals, salt has, over billions of years, accumulated in the oceans as a result of evaporation returning the fresh water to land as rain and snow. As a result, the vast bulk of the water on Earth is regarded as saline or salt water, with an average salinity of 35% (or 3.5%, roughly equivalent to 35 grams of salts in 1kg of seawater), though this varies slightly according to the amount of runoff received from surrounding land. In all, oceanic water, saline water from marginal seas, and water from saline closed lakes amounts to over 98% of the water on Earth, though no closed lake stores a globally significant amount of water. Renewable saline groundwater is believed to total at least 100 km³ globally, but is seldom considered except when evaluating water quality in arid regions.
Freshwater
[edit | edit source]

The remainder of the Earth's water constitutes the planet's fresh water resource. Typically, fresh water is defined as water with a salinity of less than 1% that of the oceans—i.e. below around 0.35%. Water with a salinity between this level and 1% is typically referred to as marginal water because it is marginal for many uses by humans and animals. The planet's fresh water is also very unevenly distributed. Although in warm periods such as the Mesozoic and Paleogene when there were no glaciers anywhere on the planet all fresh water was found in rivers and streams, today the distribution is approximately as follows:
- Ice caps and glaciers: 68.7%
- Antarctic ice cap: 90%, 9700 years renewal interval
- Greenland ice cap: 9%
- Other glaciers: <1%, 1600 years renewal interval
- Groundwater: 30.1%, 1400 year renewal interval
- Surface water: 0.3%
- Freshwater lakes:87%, 17 years renewal interval
- Swamps: 11%
- Rivers: 2%, 16 days renewal interval
- Ground ice and permafrost: 0.86%
- Atmosphere: 0.04%
Of these freshwater sources, only river water is generally valuable. Most water in lakes is in very inhospitable regions such as glacial lakes of Canada. Lake Baikal and Lake Khövsgöl, both protected from Quaternary glaciation by aridity, have equivalent amounts of water, and the latter has been used in Mongolia as a source of drinking water. Although the total volume of groundwater is known to be much greater than that of river runoff, a large proportion of this groundwater is saline and should therefore be classified with the saline water above.
There is also a lot of fossil groundwater in arid regions that has never been renewed for thousands of years; this must not be seen as renewable water. However, fresh groundwater is of great value, especially in arid countries such as India. Its distribution is broadly similar to that of surface river water, but it is easier to store in hot and dry climates because groundwater storages are much more shielded from evaporation than are dams. In countries such as Yemen, groundwater from erratic rainfall during the rainy season is the major source of irrigation water. Because groundwater recharge is much more difficult to accurately measure than surface runoff, groundwater is not generally used in areas where even fairly limited levels of surface water are available. Even today, estimates of total groundwater recharge vary greatly for the same region depending on what source is used, and cases where fossil groundwater is exploited beyond the recharge rate (including the Ogallala Aquifer) are very frequent and almost always not seriously considered when they were first developed.[1]
Properties of water
[edit | edit source]

Water appears in nature in all three common states of matter and may take many different forms on Earth: water vapor and clouds in the sky; seawater and icebergs in the polar oceans; glaciers and rivers in the mountains; and the liquid in aquifers in the ground. At high temperatures and pressures, such as in the interior of giant planets, it is argued that water exists as ionic water in which the molecules break down into a soup of hydrogen and oxygen ions, and at even higher pressures as superionic water in which the oxygen crystallises but the hydrogen ions float around freely within the oxygen lattice.
Major properties
[edit | edit source]Water is a liquid at standard temperature and pressure. It is tasteless and odorless. The intrinsic color of water and ice is a very slight blue hue, although both appear colorless in small quantities. Water vapor is essentially invisible as a gas. Water is transparent in the visible electromagnetic spectrum. Thus aquatic plants can live in water because sunlight can reach them. Ultra-violet and infrared light is strongly absorbed.[2]
Since the water molecule is not linear and the oxygen atom has a higher electronegativity than the hydrogen atoms, the oxygen carries a slight negative charge, while the hydrogen atoms are slightly positive. As a result, water is a polar molecule with an electrical dipole moment.
The maximum density of water occurs at 3.98 °C (39.16 °F). It has the anomalous property of becoming less dense, not more, when it is cooled down to its solid form, ice. It expands to occupy 9% greater volume in this solid state, which accounts for the fact of ice floating on liquid water. Its Density is 1,000 kg/m3 liquid (4 °C), and weighs 62.4 lb/ft.3 (917 kg/m3, solid). It weighs 8.3454 lb/gal (US, liquid).
The boiling point of water (and all other liquids) is dependent on the barometric pressure. For example, on the top of Mt. Everest water boils at 68 °C (154 °F), compared to 100 °C (212 °F) at sea level. Conversely, water deep in the ocean near geothermal vents can reach temperatures of hundreds of degrees and remain liquid.

Water has the second highest molar specific heat capacity of any known substance, after ammonia, as well as a high heat of vaporization (40.65 kJ·mol−1), both of which are a result of the extensive hydrogen bonding between its molecules. These two unusual properties allow water to moderate Earth's climate by buffering large fluctuations in temperature.
Solvent
[edit | edit source]Water is a good solvent and is often referred to as the universal solvent. Substances that dissolve in water, such as salts, sugars, acids, alkalis, and some gases (especially oxygen, carbon dioxide) are known as hydrophilic (water-loving) substances, while those that do not mix well with water (e.g. fats and oils), are known as hydrophobic (water-fearing) substances.
Water is miscible with many liquids, such as ethanol, in all proportions, forming a single homogeneous liquid. On the other hand, water and most oils are immiscible usually forming layers according to increasing density from the top. As a gas, water vapor is completely miscible with air.
Water forms an azeotrope with many other solvents.
Conductivity
[edit | edit source]Pure water has a low electrical conductivity, but this increases significantly with the dissolution of a small amount of ionic material such as sodium chloride.
Water can be split by electrolysis into hydrogen and oxygen. As an oxide of hydrogen, water is formed when hydrogen or hydrogen-containing compounds burn or react with oxygen or oxygen-containing compounds. Water is not a fuel, it is an end-product of the combustion of hydrogen. The energy required to split water into hydrogen and oxygen by electrolysis or any other means is greater than the energy that can be collected when the hydrogen and oxygen recombine. Elements which are more electropositive than hydrogen such as lithium, sodium, calcium, potassium and caesium displace hydrogen from water, forming hydroxides. Being a flammable gas, the hydrogen given off is dangerous and the reaction of water with the more electropositive of these elements may be violently explosive.
In biological systems
[edit | edit source]All the major components in cells (proteins, DNA and polysaccharides) are also dissolved in water. Water is fundamental to photosynthesis and respiration. Photosynthetic cells use the sun's energy to split off water's hydrogen from oxygen. Hydrogen is combined with CO2 (absorbed from air or water) to form glucose and release oxygen. All living cells use such fuels and oxidize the hydrogen and carbon to capture the sun's energy and reform water and CO2 in the process (cellular respiration).
Hydrogen bonding in water
[edit | edit source]Water can form an unusually large number of intermolecular hydrogen bonds (four) for a molecule of its size. These factors lead to strong attractive forces between molecules of water, giving rise to water's high surface tension and capillary forces. The capillary action refers to the tendency of water to move up a narrow tube against the force of gravity. This property is relied upon by all vascular plants, such as trees.[3]
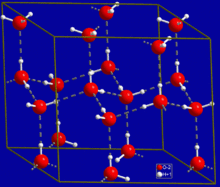

The most ubiquitous, and perhaps simplest, example of a hydrogen bond is found between water molecules. In a discrete water molecule, there are two hydrogen atoms and one oxygen atom. Two molecules of water can form a hydrogen bond between them; the simplest case, when only two molecules are present, is called the water dimer and is often used as a model system. When more molecules are present, as is the case of liquid water, more bonds are possible because the oxygen of one water molecule has two lone pairs of electrons, each of which can form a hydrogen bond with a hydrogen on another water molecule. This can repeat such that every water molecule is H-bonded with up to four other molecules, as shown in the figure (two through its two lone pairs, and two through its two hydrogen atoms). Hydrogen bonding strongly affects the crystal structure of ice, helping to create an open hexagonal lattice. The density of ice is less than water at the same temperature; thus, the solid phase of water floats on the liquid, unlike most other substances. Liquid water's high boiling point is due to the high number of hydrogen bonds each molecule can form relative to its low molecular mass. Owing to the difficulty of breaking these bonds, water has a very high boiling point, melting point, and viscosity compared to otherwise similar liquids not conjoined by hydrogen bonds. Water is unique because its oxygen atom has two lone pairs and two hydrogen atoms, meaning that the total number of bonds of a water molecule is up to four. For example, hydrogen fluoride—which has three lone pairs on the F atom but only one H atom—can form only two bonds; (ammonia has the opposite problem: three hydrogen atoms but only one lone pair). H-F...H-F...H-F The exact number of hydrogen bonds formed by a molecule of liquid water fluctuates with time and depends on the temperature. From TIP4P liquid water simulations at 25 °C, it was estimated that each water molecule participates in an average of 3.59 hydrogen bonds. At 100 °C, this number decreases to 3.24 due to the increased molecular motion and decreased density, while at 0 °C, the average number of hydrogen bonds increases to 3.69. A more recent study found a much smaller number of hydrogen bonds: 2.357 at 25 °C. The differences may be due to the use of a different method for defining and counting the hydrogen bonds. Where the bond strengths are more equivalent, one might instead find the atoms of two interacting water molecules partitioned into two polyatomic ions of opposite charge, specifically hydroxide (OH−) and hydronium (H3O+). (Hydronium ions are also known as 'hydroxonium' ions.) H-O− H3O+ Indeed, in pure water under conditions of standard temperature and pressure, this latter formulation is applicable only rarely; on average about one in every 5.5 × 108 molecules gives up a proton to another water molecule, in accordance with the value of the dissociation constant for water under such conditions. It is a crucial part of the uniqueness of water.[4]
Strong acids and bases
[edit | edit source]Water is also central to acid-base neutrality and enzyme function. An acid, a hydrogen ion (H+, that is, a proton) donor, can be neutralized by a base, a proton acceptor such as hydroxide ion (OH−) to form water. Water is considered to be neutral, with a pH (the negative log of the hydrogen ion concentration) of 7. Acids have pH values less than 7 while bases have values greater than 7.[5]
Strong acids and bases are those that, for practical purposes, completely dissociated (ionize) in water. Hydrochloric acid (HCl) is a good example of a strong acid.
A commonly encountered problem is to calculate the pH of a solution of a given concentration of a strong acid. Normally, the concentration of the acid will be very high compared to the baseline concentration of H+ ions in pure water, which is 10−7 molar. Under these conditions, the H+ ion concentration is very nearly that of the acid concentration, and the pH is calculated simply by taking the negative logarithm of that value[6]
For example, for a 0.01M solution of HCl, the H+ concentration can be taken as 0.01M, and the pH is −log(0.01). That is, pH = 2.
For very weak concentrations, i.e. concentrations around 10−6M or less, the baseline concentration of H+ ions in pure water becomes significant, and must be taken into account.[7] A method of solution is as follows. At equilibrium, any aqueous solution must satisfy the dissociation equilibrium equation for water[8],
Another constraint is that the nominal concentration of the acid must be preserved. The nominal concentration is designated Ca, and is equivalent to the amount of acid that is initially added to the reaction. This is known as the mass balance equation, and can be written,
Where "HA" refers to the protonated form of the acid, and "A–" to the conjugate base anion.
Note that for a given reaction, Ca is constant. This equation is merely saying that the molecules of acid can either be protonated or ionized, but that the total number will stay the same.
For a strong acid which is completely dissociated, [A–] >> [HA], and the [HA] term can be dropped:
Another relationship that must be satisfied is known as the electroneutrality principle, or the charge balance equation, and is the statement that the total charge of the solution must be zero. So the sum of all the negative ion charges must equal the sum of the positive ion charges. This can be written,
For a strong acid, one can use Ca in place of [A–], and eliminate [OH–] from this equation by substituting the value derived from the equilibrium equation for water, [OH–] = Kw / [H+]. Thus,
Putting this into the form of a quadratic equation,
Which is readily solved for [H+].
For example, to find the pH of a solution of 5×10−8M of HCl, first note that this concentration is small compared to the baseline concentration of [H+] in water (10−7). So the quadratic equation derived above should be used.
Weak acids and weak bases
[edit | edit source]The problem in this case would be to determine the pH of a solution of a specific concentration of an acid, when that acid's pKa or Ka (acid dissociation constant) is given.
In this case, the acid is not completely dissociated, but the degree of dissociation is given by the equilibrium equation for that acid:
The mass balance and charge balance equations can be applied here as well, but in the case of a weak acid, the acid is not completely dissociated, and thus the assumption [A–] >> [HA] is not valid. Therefore the mass balance equation is
Unless the acid is very weak, or the concentration is very dilute, it it reasonable to assume that the concentration of [H+] is much greater than the concentration of [OH–]. This assumption simplifies the calculation and can be verified after the result is found. Note that this is equivalent to the assumption that the pH value is lower than about 6. With this assumption, the charge balance equation is
There are three equations with three unknowns ([H+], [A–], and [HA]), which need to be solved for [H+]. The mass balance equation allows to solve for [HA] in terms of [H+]:
And then plug these into the equilibrium equation for the acid
Rearrange this to put it in the form of a quadratic equation,
The ICE table allows to evaluate the differences in concentrations before and after the reaction – basically, it is a mnemonic device for implementing the mass balance and charge balance equations for a given reaction, by accounting for the movements of the acid molecules and the charges. The equation derived by using the ICE table is the same as the quadratic equation given above.
For example, consider a problem of finding the pH of a 0.01M solution of benzoic acid, given that, for this acid, Ka = 6.5×10−5 (pKa = 4.19).
The equilibrium equation for this reaction is
One can neglect the [OH–] concentration, hoping that the final answer will by pH < 6. Then [H+] = [A–], and the equilibrium equation becomes
The mass balance equation is
Solving for [HA] yields
and plugging that into the equilibrium equation, results in the quadratic equation
Which gives the answer
Thus the assumption that pH < 6 was valid, and the [OH–] concentration might well be ignored.

Acid dissociation constant and pKa
[edit | edit source]An acid dissociation constant, Ka, (also known as acidity constant, or acid-ionization constant) is a quantitative measure of the strength of an acid in solution. It is the equilibrium constant for a chemical reaction known as dissociation in the context of acid-base reactions. The equilibrium can be written symbolically as:
- HA = A− + H+,
where HA is a generic acid that dissociates by splitting into A−, known as the conjugate base of the acid, and the hydrogen ion or proton, H+, which, in the case of aqueous solutions, exists as a solvated hydronium ion. In the example shown in the figure, HA represents acetic acid, and A− the acetate ion. The chemical species HA, A− and H+ are said to be in equilibrium when their concentrations do not change with the passing of time. The dissociation constant is usually written as a quotient of the equilibrium concentrations (in mol/L), denoted by [HA], [A−] and [H+]:
Due to the many orders of magnitude spanned by Ka values, a logarithmic measure of the acid dissociation constant is more commonly used in practice. pKa, which is equal to −log10 Ka, may also be (incorrectly) referred to as an acid dissociation constant:
In the case of multiple pK values they are designated by indices: pK1, pK2, pK3 and so on. For amino acids, the pK1 constant refers to its carboxyl (-COOH) group, pK2 refers to its amino (-NH3) group and the pK3 is the pK value of its side chain.
According to Arrhenius's original definition, an acid is a substance that dissociates in aqueous solution, releasing the hydrogen ion H+ (a proton):[9]
- HA = A− + H+.
The equilibrium constant for this dissociation reaction is known as a dissociation constant. The liberated proton combines with a water molecule to give a hydronium (or oxonium) ion H3O+, and so Arrhenius later proposed that the dissociation should be written as an acid–base reaction:
- HA + H2O = A− + H3O+.
Brønsted and Lowry generalised this further to a proton exchange reaction:[10][11][12]
- acid + base = conjugate base + conjugate acid.
The acid loses a proton, leaving a conjugate base; the proton is transferred to the base, creating a conjugate acid. For aqueous solutions of an acid HA, the base is water; the conjugate base is A− and the conjugate acid is the hydronium ion. The Brønsted–Lowry definition applies to other solvents, such as dimethyl sulfoxide: the solvent S acts as a base, accepting a proton and forming the conjugate acid SH+.
In solution chemistry, it is common to use H+ as an abbreviation for the solvated hydrogen ion, regardless of the solvent. In aqueous solution H+ denotes a solvated hydronium ion rather than a proton.[13][14]
The designation of an acid or base as "conjugate" depends on the context. The conjugate acid BH+ of a base B dissociates according to
- BH+ + OH− = B + H2O
which is the reverse of the equilibrium
- H2O (acid) + B (base) = OH− (conjugate base) + BH+ (conjugate acid).
The hydroxide ion OH−, a well known base, is here acting as the conjugate base of the acid water. Acids and bases are thus regarded simply as donors and acceptors of protons respectively.
A broader definition of acid dissociation includes hydrolysis, in which protons are produced by the splitting of water molecules. For example, boric acid (B(OH)3) acts as a weak acid, even though it is not a proton donor, because of the hydrolysis equilibrium
- B(OH)3 + 2 H2O = B(OH)4− + H3O+.
Similarly, metal ion hydrolysis causes ions such as [Al(H2O)6]3+ to behave as weak acids:[15]
- [Al(H2O)6]3+ +H2O =} [Al(H2O)5(OH)]2+ + H3O+.
pKa values of different amino acids are given in the table.
| Amino Acid | Short | Abbrev. | Avg. Mass (Da) | pI | pK1 (α-COOH) |
pK2 (α-+NH3) |
|---|---|---|---|---|---|---|
| Alanine | A | Ala | 89.09404 | 6.01 | 2.35 | 9.87 |
| Cysteine | C | Cys | 121.15404 | 5.05 | 1.92 | 10.70 |
| Aspartic acid | D | Asp | 133.10384 | 2.85 | 1.99 | 9.90 |
| Glutamic acid | E | Glu | 147.13074 | 3.15 | 2.10 | 9.47 |
| Phenylalanine | F | Phe | 165.19184 | 5.49 | 2.20 | 9.31 |
| Glycine | G | Gly | 75.06714 | 6.06 | 2.35 | 9.78 |
| Histidine | H | His | 155.15634 | 7.60 | 1.80 | 9.33 |
| Isoleucine | I | Ile | 131.17464 | 6.05 | 2.32 | 9.76 |
| Lysine | K | Lys | 146.18934 | 9.60 | 2.16 | 9.06 |
| Leucine | L | Leu | 131.17464 | 6.01 | 2.33 | 9.74 |
| Methionine | M | Met | 149.20784 | 5.74 | 2.13 | 9.28 |
| Asparagine | N | Asn | 132.11904 | 5.41 | 2.14 | 8.72 |
| Pyrrolysine | O | Pyl | ||||
| Proline | P | Pro | 115.13194 | 6.30 | 1.95 | 10.64 |
| Glutamine | Q | Gln | 146.14594 | 5.65 | 2.17 | 9.13 |
| Arginine | R | Arg | 174.20274 | 10.76 | 1.82 | 8.99 |
| Serine | S | Ser | 105.09344 | 5.68 | 2.19 | 9.21 |
| Threonine | T | Thr | 119.12034 | 5.60 | 2.09 | 9.10 |
| Selenocysteine | U | Sec | 168.053 | |||
| Valine | V | Val | 117.14784 | 6.00 | 2.39 | 9.74 |
| Tryptophan | W | Trp | 204.22844 | 5.89 | 2.46 | 9.41 |
| Tyrosine | Y | Tyr | 181.19124 | 5.64 | 2.20 | 9.21 |
Henderson–Hasselbalch equation
[edit | edit source]Lawrence Joseph Henderson wrote an equation, in 1908, describing the use of carbonic acid as a buffer solution. Karl Albert Hasselbalch later re-expressed that formula in logarithmic terms, resulting in the Henderson–Hasselbalch equation . Hasselbalch was using the formula to study metabolic acidosis.
The Henderson–Hasselbalch equation is derived from the acid dissociation constant equation by the following steps[16][17]:
or
The ratio is unitless, and as such, other ratios with other units may be used. For example, the mole ratio of the components, or the fractional concentrations where will yield the same answer. Sometimes these other units are more convenient to use.
pKa and gibbs free energy
[edit | edit source]An equilibrium constant is related to the standard Gibbs energy change for the reaction, so for an acid dissociation constant
R is the gas constant and T is the absolute temperature. Note that pKa= −log Ka and 2.303 ≈ ln 10. At 25 °C ΔG![]() in kJ·mol−1 = 5.708 pKa (1 kJ·mol−1 = 1000 Joules per mole). Free energy is made up of an enthalpy term and an entropy term.[18]
in kJ·mol−1 = 5.708 pKa (1 kJ·mol−1 = 1000 Joules per mole). Free energy is made up of an enthalpy term and an entropy term.[18]
The standard enthalpy change can be determined by calorimetry or by using the van 't Hoff equation, though the calorimetric method is preferable. When both the standard enthalpy change and acid dissociation constant have been determined, the standard entropy change is easily calculated from the equation above. In the following table, the entropy terms are calculated from the experimental values of pKa and ΔH![]() . The data were critically selected and refer to 25 °C and zero ionic strength, in water.[18]
. The data were critically selected and refer to 25 °C and zero ionic strength, in water.[18]
| Compound | Equilibrium | pKa | ΔG |
ΔH |
—TΔS |
|---|---|---|---|---|---|
| HA = Acetic acid | HA = H+ + A− | 4.756 | 22.147† | −0.41 | 22.56‡ |
| H2A+ = GlycineH+ | H2A+ = HA + H+ | 2.351 | 13.420 | 4.00 | 9.419 |
| HA = H+ + A− | 9.78 | 55.825 | 44.20 | 11.6 | |
| H2A = Maleic acid | H2A = HA− + H+ | 1.92 | 10.76 | 1.10 | 9.85 |
| HA− = H+ + A2− | 6.27 | 35.79 | −3.60 | 39.4 | |
| H3A = Citric acid | H3A = H2A− + H+ | 3.128 | 17.855 | 4.07 | 13.78 |
| H2A− = HA2− + H+ | 4.76 | 27.176 | 2.23 | 24.9 | |
| HA2− = A3− + H+ | 6.40 | 36.509 | −3.38 | 39.9 | |
| Boric acid | B(OH)3 + H2O ↔ [B(OH)4]- + H+ | 9.237 | 52.725 | 13.80 | 38.92 |
| H3A = Phosphoric acid | H3A ↔ H2A− + H+ | 2.148 | 12.261 | −8.00 | 20.26 |
| H2A− = HA2− + H+ | 7.20 | 41.087 | 3.60 | 37.5 | |
| HA2− = A3− + H+ | 12.35 | 80.49 | 16.00 | 54.49 | |
| Hydrogen sulfate | HA− ↔ A2− + H+ | 1.99 | 11.36 | −22.40 | 33.74 |
| H2A = Oxalic acid | H2A ↔ HA− + H+ | 1.27 | 7.27 | −3.90 | 11.15 |
| HA− = A2− + H+ | 4.266 | 24.351 | 7.00 | 31.35 |
Buffers
[edit | edit source]Buffer solutions achieve their resistance to pH change because of the presence of an equilibrium between the acid HA and its conjugate base A-. HA = H+ + A- When some strong acid is added to an equilibrium mixture of the weak acid and its conjugate base, the equilibrium is shifted to the left, in accordance with Le Chatelier's principle. Because of this, the hydrogen ion concentration increases by less than the amount expected for the quantity of strong acid added. Similarly, if strong alkali is added to the mixture the hydrogen ion concentration decreases by less than the amount expected for the quantity of alkali added. The effect is illustrated by the simulated titration of a weak acid with pKa = 4.7. The relative concentration of undissociated acid is shown in blue and of its conjugate base in red. The pH changes relatively slowly in the buffer region, pH = pKa ± 1, centered at pH = 4.7 where [HA] = [A-], but once the acid is more than 95% deprotonated the pH rises much more rapidly.[19]
Buffer solutions are necessary to keep the correct pH for enzymes in many organisms to work. Many enzymes work only under very precise conditions; if the pH moves outside of a narrow range, the enzymes slow or stop working and can denature, thus permanently disabling their catalytic activity. A buffer of carbonic acid (H2CO3) and bicarbonate (HCO3−) is present in blood plasma, to maintain a pH between 7.35 and 7.45. Industrially, buffer solutions are used in fermentation processes and in setting the correct conditions for dyes used in colouring fabrics. They are also used in chemical analysis and calibration of pH meters. The majority of biological samples that are used in research are made in buffers, especially phosphate buffered saline (PBS) at pH 7.4.[20]
Common buffer compounds used in biology[21]
[edit | edit source]| Common Name | pKa at 25°C |
Buffer Range | Temp Effect dpH/dT in (1/K) ** |
Mol. Weight |
Full Compound Name |
|---|---|---|---|---|---|
| TAPS | 8.43 | 7.7–9.1 | −0.018 | 243.3 | 3-{[tris(hydroxymethyl)methyl]amino}propanesulfonic acid |
| Bicine | 8.35 | 7.6–9.0 | −0.018 | 163.2 | N,N-bis(2-hydroxyethyl)glycine |
| Tris | 8.06 | 7.5–9.0 | −0.028 | 121.14 | tris(hydroxymethyl)methylamine |
| Tricine | 8.05 | 7.4–8.8 | −0.021 | 179.2 | N-tris(hydroxymethyl)methylglycine |
| TAPSO | 7.635 | 7.0-8.2 | 259.3 | 3-[N-Tris(hydroxymethyl)methylamino]-2-hydroxypropanesulfonic Acid | |
| HEPES | 7.55 | 6.8–8.2 | −0.014 | 238.3 | 4-2-hydroxyethyl-1-piperazineethanesulfonic acid |
| TES | 7.40 | 6.8–8.2 | −0.020 | 229.20 | 2-{[tris(hydroxymethyl)methyl]amino}ethanesulfonic acid |
| MOPS | 7.20 | 6.5–7.9 | −0.015 | 209.3 | 3-(N-morpholino)propanesulfonic acid |
| PIPES | 6.76 | 6.1–7.5 | −0.008 | 302.4 | piperazine-N,N′-bis(2-ethanesulfonic acid) |
| Cacodylate | 6.27 | 5.0–7.4 | 138.0 | dimethylarsinic acid | |
| SSC | 7.0 | 6.5-7.5 | 189.1 | saline sodium citrate | |
| MES | 6.15 | 5.5–6.7 | −0.011 | 195.2 | 2-(N-morpholino)ethanesulfonic acid |
** Values are approximate.
What is pH?
[edit | edit source]The concept of p[H] was first introduced by Danish chemist Søren Peder Lauritz Sørensen at the Carlsberg Laboratory in 1909 and revised to the modern pH in 1924 after it became apparent that electromotive force in cells depends on activity rather than concentration of hydrogen ions. In the first papers, the notation had the H as a subscript to the lowercase p, like so: pH. It is unknown what the exact definition of 'p' in pH is. A common definition often used in schools is "percentage". However some references suggest the p stands for “Power”, others refer to the German word “Potenz” (meaning power in German), still others refer to “potential”. Jens Norby published a paper in 2000 arguing that p is a constant and stands for “negative logarithm”; H then stands for Hydrogen. According to the Carlsberg Foundation pH stands for "power of hydrogen". Other suggestions that have surfaced over the years are that the p stands for puissance (also meaning power, but, then, the Carlsberg Laboratory was French-speaking) or that pH stands for the Latin terms pondus Hydrogenii or potentia hydrogenii. It is also suggested that Sørensen used the letters p and q (commonly paired letters in mathematics) simply to label the test solution (p) and the reference solution (q)[22].

Pure (neutral) water has a pH around 7 at 25 °C (77 °F); this value varies with temperature. When an acid is dissolved in water, the pH will be less than 7 (if at 25 °C (77 °F)). When a base, or alkali, is dissolved in water, the pH will be greater than 7 (if at 25 °C (77 °F)). A solution of a strong acid, such as hydrochloric acid, at concentration 1 mol dm−3 has a pH of 0. A solution of a strong alkali, such as sodium hydroxide, at concentration 1 mol dm−3, has a pH of 14. Thus, measured pH values will lie mostly in the range 0 to 14. Since pH is a logarithmic scale, a difference of one pH unit is equivalent to a tenfold difference in hydrogen ion concentration[23].
Because the glass electrode (and other ion selective electrodes) responds to activity, the electrode should be calibrated in a medium similar to the one being investigated. For instance, if one wishes to measure the pH of a seawater sample, the electrode should be calibrated in a solution resembling seawater in its chemical composition, as detailed below.
An approximate measure of pH may be obtained by using a pH indicator. A pH indicator is a substance that changes color around a particular pH value. It is a weak acid or weak base and the color change occurs around 1 pH unit either side of its acid dissociation constant, or pKa, value. For example, the naturally occurring indicator litmus is red in acidic solutions (pH<7 at 25 °C (77 °F)) and blue in alkaline (pH>7 at 25 °C (77 °F)) solutions. Universal indicator consists of a mixture of indicators such that there is a continuous color change from about pH 2 to pH 10. Universal indicator paper is simple paper that has been impregnated with universal indicator.[24]
| Indicator | Low pH color | Transition pH range | High pH color |
|---|---|---|---|
| Thymol blue (first transition) | Red | 1.2 – 2.8 | Yellow |
| Methyl red | Red | 4.4 – 6.2 | Yellow |
| Bromothymol blue | Yellow | 6.0 – 7.6 | Blue |
| Thymol blue (second transition) | Yellow | 8.0 – 9.6 | Blue |
| Phenolphthalein | Colorless | 8.3 – 10.0 | Fuchsia |
A solution whose pH is 7 (at 25 °C (77 °F)) is said to be neutral, that is, it is neither acidic nor basic. Water is subject to a self-ionization process.
- H2O = H+ + OH−
The dissociation constant, KW, has a value of about 10−14, so, in neutral solution of a salt, both the hydrogen ion concentration and hydroxide ion concentration are about 10−7 mol dm−3. The pH of pure water decreases with increasing temperatures. For example, the pH of pure water at 50 °C is 6.55. Note, however, that water that has been exposed to air is mildly acidic. This is because water absorbs carbon dioxide from the air, which is then slowly converted into carbonic acid, which dissociates to liberate hydrogen ions:
- CO2 + H2O = H2CO3 = HCO3− + H+
Mathematical definition
[edit | edit source]pH is defined as a negative decimal logarithm of the hydrogen ion activity in a solution.[25]
where aH is the activity of hydrogen ions in units of Mol/L (molar concentration). Activity has a sense of concentration, however activity is always less than the concentration and is defined as a concentration (Mol/L) of an ion multiplied by activity coefficient. The activity coefficient for diluted solutions is a real number between 0 and 1 (for concentrated solutions may be greater than 1) and it depends on many parameters of a solution, such as nature of ion, ion force, temperature, etc. For a strong electrolyte, activity of an ion approaches its concentration in diluted solutions. Activity can be measured experimentally by means of an ion-selective electrode that responds, according to the Nernst equation, to hydrogen ion activity. pH is commonly measured by means of a glass electrode connected to a milli-voltmeter with very high input impedance, which measures the potential difference, or electromotive force, E, between an electrode sensitive to the hydrogen ion activity and a reference electrode, such as a calomel electrode or a silver chloride electrode. Quite often, glass electrode is combined with the reference electrode and a temperature sensor in one body. The glass electrode can be described (to 95–99.9% accuracy) by the Nernst equation[26]:
where E is a measured potential , E0 is the standard electrode potential, that is, the electrode potential for the standard state in which the activity is one. R is the gas constant, T is the temperature in kelvins, F is the Faraday constant, and n is the number of electrons transferred (ion charge), one in this instance. The electrode potential, E, is proportional to the logarithm of the hydrogen ion activity.
This definition, by itself, is wholly impractical, because the hydrogen ion activity is the product of the concentration and an activity coefficient. To get proper results, the electrode must be calibrated using standard solutions of known activity.
The operational definition of pH is officially defined by International Standard ISO 31-8 as follows:[27] For a solution X, first measure the electromotive force EX of the galvanic cell
- reference electrode|concentrated solution of KCl || solution X|H2|Pt
and then also measure the electromotive force ES of a galvanic cell that differs from the above one only by the replacement of the solution X of unknown pH, pH(X), by a solution S of a known standard pH, pH(S). The pH of X is then
The difference between the pH of solution X and the pH of the standard solution depends only on the difference between two measured potentials. Thus, pH is obtained from a potential measured with an electrode calibrated against one or more pH standards; a pH meter setting is adjusted such that the meter reading for a solution of a standard is equal to the value pH(S). Values pH(S) for a range of standard solutions S, along with further details, are given in the IUPAC recommendations.[28] The standard solutions are often described as standard buffer solution. In practice, it is better to use two or more standard buffers to allow for small deviations from Nernst-law ideality in real electrodes. Note that, because the temperature occurs in the defining equations, the pH of a solution is temperature-dependent.
Measurement of extremely low pH values, such as some very acidic mine waters,[29] requires special procedures. Calibration of the electrode in such cases can be done with standard solutions of concentrated sulfuric acid, whose pH values can be calculated with using Pitzer parameters to calculate activity coefficients.[30]
pH is an example of an acidity function. Hydrogen ion concentrations can be measured in non-aqueous solvents, but this leads, in effect, to a different acidity function, because the standard state for a non-aqueous solvent is different from the standard state for water. Superacids are a class of non-aqueous acids for which the Hammett acidity function, H0, has been developed.[31]
p[H]
[edit | edit source]This was the original definition of Sørensen, which was superseded in favour of pH in 1924. However, it is possible to measure the concentration of hydrogen ions directly, if the electrode is calibrated in terms of hydrogen ion concentrations. One way to do this, which has been used extensively, is to titrate a solution of known concentration of a strong acid with a solution of known concentration of strong alkali in the presence of a relatively high concentration of background electrolyte. Since the concentrations of acid and alkali are known, it is easy to calculate the concentration of hydrogen ions so that the measured potential can be correlated with concentrations. The calibration is usually carried out using a Gran plot.[32] The calibration yieds a value for the standard electrode potential, E0, and a slope factor, f, so that the Nernst equation in the form
can be used to derive hydrogen ion concentrations from experimental measurements of E. The slope factor is usually slightly less than one. A slope factor of less than 0.95 indicates that the electrode is not functioning correctly. The presence of background electrolyte ensures that the hydrogen ion activity coefficient is effectively constant during the titration. As it is constant, its value can be set to one by defining the standard state as being the solution containing the background electrolyte. Thus, the effect of using this procedure is to make activity equal to the numerical value of concentration.[33]
The difference between p[H] and pH is quite small. It has been stated Section 13.23, "Determination of pH"</ref> that pH = p[H] + 0.04. It is common practice to use the term "pH" for both types of measurement.
| Compartment | pH |
|---|---|
| Gastric acid | 1 |
| Lysosomes | 4.5 |
| Granules of chromaffin cells | 5.5 |
| Human skin | 5.5 |
| Urine | 6.0 |
| Neutral H2O at 37 °C | 6.81 |
| Cytosol | 7.2 |
| Cerebrospinal fluid (CSF) | 7.3 |
| Blood | 7.34–7.45 |
| Mitochondrial matrix | 7.5 |
| Pancreas secretions | 8.1 |
pOH
[edit | edit source]pOH is sometimes used as a measure of the concentration of hydroxide ions, OH−, or alkalinity. pOH is not measured independently, but is derived from pH. The concentration of hydroxide ions in water is related to the concentration of hydrogen ions by
- [OH−] = KW /[H+]
where KW is the self-ionisation constant of water. Taking cologarithms
- pOH = pKW − pH.
So, at room temperature pOH ≈ 14 − pH. However this relationship is not strictly valid in other circumstances, such as in measurements of soil alkalinity.

The pH of different cellular compartments, body fluids, and organs is usually tightly regulated in a process called acid-base homeostasis.
The pH of blood is usually slightly basic with a value of pH 7.365. This value is often referred to as physiological pH in biology and medicine.
Plaque can create a local acidic environment that can result in tooth decay by demineralisation.
Enzymes and other proteins have an optimum pH range and can become inactivated or denatured outside this range.
The most common disorder in acid-base homeostasis is acidosis, which means an acid overload in the body, generally defined by pH falling below 7.35.
In the blood, pH can be estimated from known base excess (be) and bicarbonate concentration (HCO3) by the following equation:[35]
References
[edit | edit source]- ↑ http://en.wikipedia.org/w/index.php?title=Water_distribution_on_Earth&oldid=422307996
- ↑ http://en.wikipedia.org/w/index.php?title=Water&oldid=424911919M
- ↑ http://en.wikipedia.org/w/index.php?title=Water&oldid=424911919M
- ↑ http://en.wikipedia.org/w/index.php?title=Hydrogen_bond&oldid=424341258
- ↑ http://en.wikipedia.org/w/index.php?title=Water&oldid=424911919M
- ↑ Lower, Stephen K. Chem1 Virtual Textbook, Acid-base Equilibria and Calculations (PDF). pp. 12ff.
- ↑ Maloney, Chris. "pH calculation of a very small concentration of a strong acid". Retrieved 13 March 2011.
- ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ Miessler, G. (1991). Inorganic Chemistry (2nd ed.). Prentice Hall. ISBN 0134656598. Chapter 6: Acid-Base and Donor-Acceptor Chemistry
- ↑ Bell, R.P. (1973). The Proton in Chemistry (2nd ed.). London: Chapman & Hall. ISBN 0801408032. Includes discussion of many organic Brønsted acids.
- ↑
Shriver, D.F (1999). Inorganic Chemistry (3rd ed.). Oxford: Oxford University Press. ISBN 0198503318.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) Chapter 5: Acids and Bases - ↑ Template:Housecroft3rd Chapter 6: Acids, Bases and Ions in Aqueous Solution
- ↑
Headrick, J.M. (2005). "Spectral Signatures of Hydrated Proton Vibrations in Water Clusters". Science. 308 (5729): 1765–69. doi:10.1126/science.1113094. PMID 15961665.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑
Smiechowski, M. (2006). "Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra". J. Chem. Phys. 125 (20): 204508–204522. doi:10.1063/1.2374891. PMID 17144716.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Burgess, J. (1978). Metal Ions in Solution. Ellis Horwood. ISBN 0853120277. Section 9.1 "Acidity of Solvated Cations" lists many pKa values.
- ↑ http://en.wikipedia.org/w/index.php?title=Henderson%E2%80%93Hasselbalch_equation&oldid=420194921
- ↑ Lawrence J. Henderson (1 May 1908). "Concerning the relationship between the strength of acids and their capacity to preserve neutrality" (Abstract). Am. J. Physiol. 21 (4): 173–179.
- ↑ a b
Goldberg, R. (2002). "Thermodynamic Quantities for the Ionization Reactions of Buffers" (PDF). J. Phys. Chem. Ref. Data. 31 (2): 231–370. doi:10.1063/1.1416902.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ http://en.wikipedia.org/w/index.php?title=Buffer_solution&oldid=422587570
- ↑ http://en.wikipedia.org/w/index.php?title=Buffer_solution&oldid=422587570
- ↑ http://en.wikipedia.org/w/index.php?title=Buffer_solution&oldid=422587570
- ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ "pH". IUPAC Goldbook.
- ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ Quantities and units – Part 8: Physical chemistry and molecular physics, Annex C (normative): pH. International Organization for Standardization, 1992.
- ↑ Covington, A. K.; Bates, R. G.; Durst, R. A. (1985). "Definitions of pH scales, standard reference values, measurement of pH, and related terminology" (PDF). Pure Appl. Chem. 57: 531–542. doi:10.1351/pac198557030531.
- ↑ Nordstrom, Darrell Kirk; Alpers, Charles N.; Ptacek, Carol J.; Blowes, David W. (2000). "Negative pH and Extremely Acidic Mine Waters from Iron Mountain, California". Environmental Science & Technology. 34: 254. doi:10.1021/es990646v.
- ↑ Zemaitis, J.F. (1986). "4". Handbook of Aqueous Electrolyte Thermodynamics: Theory & Application. Wiley. ISBN 0816903506.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ Rossotti, F.J.C. (1965). "Potentiometric titrations using Gran plots: A textbook omission". J. Chem. Ed. 42: 375–378. doi:10.1021/ed042p375.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ http://en.wikipedia.org/w/index.php?title=PH&oldid=424276341
- ↑ Boron, Walter, F. (2004). Medical Physiology: A Cellular And Molecular Approaoch. Elsevier/Saunders. ISBN 1-4160-2328-3.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Medical Calculators > Calculated Bicarbonate & Base Excess teven Pon, MD, Weill Medical College of Cornell University
![{\displaystyle [H^{+}][OH^{-}]=K_{w}=10^{-14}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591675fad122ab16d26dd6b88d7c6994a04237bd)
![{\displaystyle C_{a}=[HA]+[A^{-}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cf22c86382302ed93a96c2b55b352f714360508)
![{\displaystyle C_{a}=[A^{-}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f232752d4671c47d677dc300783381b93551443)
![{\displaystyle [H^{+}]=[A^{-}]+[OH^{-}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee82574eadc6b95dacf43cb5bae3edcca1c6f8b)
![{\displaystyle [H^{+}]=C_{a}+{\frac {K_{w}}{[H^{+}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18bf1efcb4482af2a3e2b61da86dfaede2845ed4)
![{\displaystyle [H^{+}]^{2}-C_{a}[H^{+}]-K_{w}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/571a7b8174233ca8546858752e9969d53d2d4f63)
![{\displaystyle [H^{+}]^{2}-5\times 10^{-8}[H^{+}]-10^{-14}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9405647acf8e5ea2fa038f7850436f795e518482)
![{\displaystyle [H^{+}]=1.28\times 10^{-7}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91f54eb49b3d0f07cf6ed66091747e8c36ffc7c5)

![{\displaystyle K_{a}={\frac {[H^{+}][A^{-}]}{[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83ee86c6746a584bd7b209324db405b0563af917)
![{\displaystyle [H^{+}]=[A^{-}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f360f5c6c8007d11a45de41f09ad08f35554258c)
![{\displaystyle [HA]=C_{a}-[A^{-}]=C_{a}-[H^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e729b228e4436a4b567d6801e27f5e970960950)
![{\displaystyle K_{a}={\frac {[H^{+}]^{2}}{C_{a}-[H^{+}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69a8c032997b3befd7914924fdfc75d4364e6de5)
![{\displaystyle [H^{+}]^{2}+K_{a}[H^{+}]-K_{a}C_{a}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d1ddb6d9e3cab181155c80e00b960a755cb76bb)
![{\displaystyle 6.5\times 10^{-5}={\frac {[H^{+}][A^{-}]}{[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59b8871ba3ae3910b48a0e7a1826304440257f69)
![{\displaystyle 6.5\times 10^{-5}={\frac {[H^{+}]^{2}}{[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb8142a19922fc5fa963b9fbfa4cdd38865ed76)
![{\displaystyle 0.01M=[HA]+[A^{-}]=[HA]+[H^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8519375fb3ae54eb514c547c984221afda70a5f1)
![{\displaystyle [HA]=0.01M-[H^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f76201d08c5d7ba802f025079b664b1be5c47cbb)
![{\displaystyle 6.5\times 10^{-5}={\frac {[H^{+}]^{2}}{0.01-[H^{+}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7f66625f1e965c8408fab90f539dcf043073649)
![{\displaystyle [H^{+}]^{2}+6.5\times 10^{-5}[H^{+}]-6.5\times 10^{-5}\times 0.01=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b8f82ea9b6a1fd8cf89225a251294720affd0d1)
![{\displaystyle [H^{+}]=7.74\times 10^{-4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c6e017410258fc5ad4aae16d0f6ffbf619f186)
![{\displaystyle pH=-\log[H^{+}]=3.11}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fcb274815a6b62ab4e50218aa831146f32ac3c)
![{\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)

![{\displaystyle H_{3}B\rightleftharpoons \ H^{+}+H_{2}B^{-}\qquad K_{1}={[H^{+}]\cdot [H_{2}B^{-}] \over [H_{3}B]}\qquad pK_{1}=-logK_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d5914a92ed297a5fdd3dd744cf66b0a3df51f04)
![{\displaystyle H_{2}B^{-}\rightleftharpoons \ H^{+}+HB^{-2}\qquad K_{2}={[H^{+}]\cdot [HB^{-2}] \over [H_{2}B^{-}]}\qquad pK_{2}=-logK_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cb9d92a69377536e3f6065352b3e178b0e2c283)
![{\displaystyle HB^{-2}\rightleftharpoons \ H^{+}+B^{-3}\qquad K_{3}={[H^{+}]\cdot [B^{-3}] \over [HB^{-2}]}\qquad pK_{3}=-logK_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1813f1ef33e035d1e9d6d2909348a02a1c559da2)
![{\displaystyle K_{\textrm {a}}={\frac {[{\textrm {H}}^{+}][{\textrm {A}}^{-}]}{[{\textrm {HA}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc85b5afa480f97938bbd4baa964ed4e75e0a48)
![{\displaystyle \log _{10}K_{\textrm {a}}=\log _{10}\left({\frac {[{\textrm {H}}^{+}][{\textrm {A}}^{-}]}{[{\textrm {HA}}]}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7004c33c2aa171790d891240571d988583dad93d)
![{\displaystyle \log _{10}K_{\textrm {a}}=\log _{10}[{\textrm {H}}^{+}]+\log _{10}\left({\frac {[{\textrm {A}}^{-}]}{[{\textrm {HA}}]}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3488b75b522c8ebb842b6916da9285b1d2ef4eb3)
![{\displaystyle -{\textrm {p}}K_{\textrm {a}}=-{\textrm {pH}}+\log _{10}\left({\frac {[{\textrm {A}}^{-}]}{[{\textrm {HA}}]}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19ed8899f25ad0511d5835b0b3c23c4af7bfa3b1)
![{\displaystyle {\textrm {pH}}={\textrm {p}}K_{\textrm {a}}+\log _{10}\left({\frac {[{\textrm {A}}^{-}]}{[{\textrm {HA}}]}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4eee91b3503f645a82e359503f32a5b3e8a0b9)
![{\displaystyle {\textrm {pH}}={\textrm {pK}}_{a}-\log \left({\frac {[{\textrm {HA}}]}{[{\textrm {A}}^{-}]}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f94cf8c05d9ec524ff8abfd47bb00cb906842ac)
![{\displaystyle [A^{-}]/[HA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cbdd71bac7c0090886365c329a0c5da749359bc)






![{\displaystyle E=E^{0}+f{\frac {RT}{nF}}\log _{e}[{\mbox{H}}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85584d1ffca5ec688288b919f844534e2658c011)
