Primary Mathematics/Negative numbers
Negative numbers
[edit | edit source]The intended audience for this lesson is students, whether children or adults. For the same lesson, but aimed at an audience of parents and educators, whether in traditional or home-schooling environments, please see this Wikiversity page.
Introduction
[edit | edit source]Negative numbers are numbers less than zero. A convenient way to think of them is as a number owed. For example, if you have negative four apples, that means you owe four apples to someone. A dash is typically used to indicate a negative value. In our case, we would write -4 apples.
Some other examples of negative numbers are temperatures below zero, depths below sea-level, or floors in a building below the ground. Opposites can also be used, like forward and backward (negative distance), going faster and slower (negative acceleration), give and take (giving negative quantities), and heating and cooling (adding negative heat).
Negative numbers are always shown with a minus sign (-) directly in front. Positive numbers, which haven't required a label until now, are sometimes shown with a plus sign (+) directly in front, but this is optional.
Addition involving negative numbers
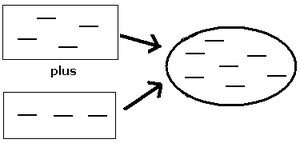
[edit | edit source]When adding two negative numbers, just find the sum and make it negative:
-4 + -3 = -7
This can be visualized by the use of negative tiles, each of which represent the number negative one (-1).
The situation gets a bit more complicated when one of the numbers to be added together is negative and the other is positive. Let's say we want to add positive two (+2) to negative three (-3). If we draw the plus and minus signs, we can pair up each positive sign with one negative sign and then they cancel each other out. This leaves one negative sign, though, meaning that +2 plus -3 equals -1:
We can write this as:
+2 + -3 = -1
It doesn't matter if we change the order in addition, so we also get:
-3 + +2 = -1
Some people skip the plus sign on positive numbers, this gives us these two equations:
2 + -3 = -1
-3 + 2 = -1
Let's review. To add two negative numbers, just add normally, then make the result negative:
-4 + -3 = -7
When adding one negative number to one positive number, it can be rewritten as a subtraction problem:
4 + -3 = 4 - 3 = 1
It may sometimes be necessary to change the order of the two terms to do this:
-3 + 4 = 4 - 3 = 1
Any subtraction problem can also produce a negative value:
-4 + 3 = 3 - 4 = -1
The last problem can be visualized as if you owed 4 apples, then got 3 (which you gave to the person to whom you owed the apples), so you would still owe them 1 apple.
Subtraction involving negative numbers
[edit | edit source]Subtracting a negative number is the same as adding the same positive number. In other words, two negative signs makes a positive:
5 - -2 = 5 + 2 = 7
Or, if both numbers are negative:
-5 - -2 = -5 + 2 = 2 - 5 = -3
To illustrate the last example, imagine five negative signs, then you subtract, or take away, two negative signs, leaving you with three negative signs:
It gets a bit trickier when you need to subtract more negatives than you start with. Here we start with one negative but need to take away four. This requires us to add three sets of positives and negatives, which cancel each other out. Then, once we remove the four negatives, that leaves us with three positives:
This means:
-1 - -4 = +3
The other method is to say, since two negative signs make a positive sign, we instead can write:
-1 + 4 = 4 - 1 = 3
Note that, unlike addition, you can't change the order in a subtraction problem, or you may get a different answer. This is true whether you are subtracting positive or negative numbers:
9 - 8 = +1
8 - 9 = -1
Multiplication involving negative numbers
[edit | edit source]Just multiply normally, then apply the following rules:
- If both numbers are negative (or both are positive), the result is positive.
- If only one number is negative, the result is negative.
Thus:
4 × 3 = 12 -4 × -3 = 12 -4 × 3 = -12 4 × -3 = -12
You can change the order in multiplication, but, unlike addition, there isn't much advantage to doing this. Here are the previous examples in the reverse order:
3 × 4 = 12 -3 × -4 = 12 3 × -4 = -12 -3 × 4 = -12
Division involving negative numbers
[edit | edit source]Just divide normally, then apply the following rules:
- If both numbers are negative (or both are positive), the result is positive.
- If only one number is negative, the result is negative.
Note that these are the same rules as were used for multiplication:
12 ÷ 3 = 4 -12 ÷ -3 = 4 12 ÷ -3 = -4 -12 ÷ 3 = -4
Here's those examples are again, using the alternate slash notation instead of the familiar division sign:
12 / 3 = 4 -12 / -3 = 4 12 / -3 = -4 -12 / 3 = -4
Note that you can't change the order in division, just like you can't in subtraction, or you get a different answer. Here are the previous examples in the reverse order:
3 / 12 = 1 / 4 -3 / -12 = 1 / 4 -3 / 12 = -1 / 4 3 / -12 = -1 / 4
Other notations
[edit | edit source]Negative numbers are sometimes shown in parenthesis, in red, or with DB (for DeBit) next to them, in the field of accounting (that is, when dealing with money).