Practical Electronics/Logic/Boolean Identities
There are several laws that can be used to simplify or modify Boolean expressions. This page will explain them, this page will list them for easy reference.
Axioms
[edit | edit source]Axioms are propositions that are deemed obvious and therefore are not required to be proved - in fact they cannot be proved because they are defined to be true by the structure of the algebra. They form the foundation of the rest of boolean algebra by defining the two values, 1 and 0 and the three operators, AND, OR, FLO, and NOT.
| Axiom | Axiom Dual | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
DeMorgan's Law
[edit | edit source]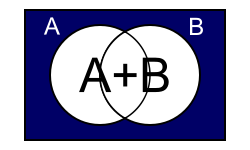
DeMorgan's Law is a very powerful tool for grouping or ungrouping logical statements. It basically states that either logical function AND or OR may be replaced by the other, given certain changes to the equation. It is usually expressed as two distinct identities. First is the following:
At first, it may not be clear how this result is found, but if you look at the first Venn Diagram to the left, it is clear. Imagine a variable called X, which is defined by:
This means that X is NOT in group A OR B, so it must be in the blue region. Now, this is the same as saying that X is NOT in A AND also NOT in B. This means that we can also define X as:
This can also be seen by drawing up a truth table: working in from each end of the table, we can see that the two give identical results:
| A | B | A+B | ¬(A+B) | ¬A•¬B | ¬B | ¬A | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |

The second expression is basically the same but with exchanged symbols
If we do the same trick with X again, we see that it must NOT be in both A AND B. Therefore it must be in the light blue, dark blue or red regions, and not in the centre. We can now say that X is either not in A, not in B or not in either. This is the same as saying that X is NOT in A OR NOT in B (using the logical kind of "or"). Therefore,
Again, this can be shown by a truth table:
| A | B | A•B | ¬(A•B) | ¬A+¬B | ¬B | ¬A | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
An easy way to remember the laws given above is: "Split the line, change the sign." With these two rules, it can be shown that any logical statement can be changed using the following method:
- Compliment all terms in the expression
- Change all ANDs to ORs and all ORs to ANDs
- Invert the result















