Physics Textbook/Light
What is light
[edit | edit source]Light is electromagnetic radiation with a wavelength that is visible to the eye, or in a more general sense, any electromagnetic radiation in the range from infrared to ultraviolet. The three basic dimensions of light (and of all electromagnetic radiation) are:
- intensity (or brilliance or amplitude, perceived by humans as the brightness of the light),
- frequency (or wavelength, perceived by humans as the color of the light), and
- polarization (or angle of vibration and not perceivable by humans under ordinary circumstances)
Due to wave-particle duality, light simultaneously exhibits properties of both waves and particles.
Wave-particle duality
[edit | edit source]The modern theory that explains the nature of light is wave-particle duality, described by Albert Einstein in the early 1900s, based on his work on the photoelectric effect and Planck's results. Einstein determined that the energy of a photon is proportional to its frequency. More generally, the theory states that everything has both a particle nature, and a wave nature, and various experiments can be done to bring out one or the other. The particle nature is more easily discerned if an object has a large mass, so it took until an experiment by Louis de Broglie in 1924 to realise that electrons also exhibited wave-particle duality. Einstein received the Nobel Prize in 1921 for his work with the wave-particle duality on photons, and de Broglie followed in 1929 for his extension to other particles.
Color and wavelengths
[edit | edit source]The different wavelengths are detected by the human eye and then interpreted by the human brain as colors, ranging from red at the longest wavelengths (lowest frequencies) to violet at the shortest wavelengths (highest frequencies). The intervening frequencies are seen as orange, yellow, green, blue, and, conventionally, indigo.

The wavelengths of the electromagnetic spectrum immediately outside the range that the human eye is able to see/detect are called ultraviolet (UV) at the short wavelength (high frequency) end and infrared (IR) at the long wavelength (low frequency) end. Although humans cannot see IR, we do perceive the near IR (shorter wavelength, higher frequency, higher energy) as heat through receptors in the skin. Cameras that can detect IR and convert it to light are called night-vision cameras.
UV radiation is not perceived by humans at all except in a very delayed fashion, as overexposure of the skin to UV light causes sunburn, or skin cancer. Some animals, such as bees, can see UV radiation while others, such as pit viper snakes, can see IR using pits in their heads.
Ray Approximation of Light
[edit | edit source]When studying refraction, mirrors and lenses we ignore the wave properties of light.
What is a ray of light?
[edit | edit source]Light acts as both a wave and a ray of particles. When observing the effects of light on large object such as cubes of glass, mirrors and lenses light can be observed to act like a ray of tiny little particles that can be bounced, directed or slowed.
Mediums slow light down -- lawn mower analogy
Mirrors bounce light -- converging mirrors, diverging mirrors
Lens direct light -- converging lens, diverging mirror lens
Reflection and Refraction
[edit | edit source]

Refraction is the change in direction of a wave due to a change in velocity. It happens when waves travel from a medium with a given refractive index to a medium with another. At the boundary between the media the wave changes direction; its wavelength increases or decreases but frequency remains constant. For example, a light ray will refract as it passes through glass; understanding of this concept led to the invention of the refracting telescope.
In the diagram on the right, ripples travel from the left and pass over a shallower region inclined at an angle to the wavefront. The waves travel more slowly in the shallower water, so the wavelength decreases and the wave bends at the boundary. The dotted line represents the normal to the boundary. The dashed line represents the original direction of the waves. The phenomenon explains why waves on a shoreline never hit the shoreline at an angle. Whichever direction the waves travel in deep water, they always refract towards the normal as they enter the shallower water near the beach.
An example of this is looking into a bowl of water. Air has a refractive index of about 1.003, and water has a refractive index of about 1.33. If you look at a straight object, such as a pencil, which is placed at a slant, partially in the water, the object appears to bend at the water's surface. This is due to the light rays from the object being bent as they move from the water to the air. This causes water to appear shallower than it really is.
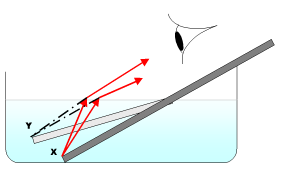
In the diagram, the dark rectangle represents the actual position of a pencil sitting in a bowl of water. The light rectangle represents the apparent position of the pencil. Notice that the end (X) looks like it is at (Y), a position that is considerably shallower than (X).
Refraction is also responsible for rainbows and for splitting up of white light into a rainbow-spectrum as it passes through a glass prism. Glass has a higher refractive index than air and the different frequencies of light travel at different speeds (dispersion), causing them to be refracted at different angles. The different frequencies correspond to different colours observed.
The amount that the light bends during refraction is calculated using Snell's law.
Recently some metamaterials have been created which have a negative refractive index.
f=f
[edit | edit source]Frequency is fundamental
The speed of light doesn't ever change.
The frequency and wavelength (λ) of light can change.

Frequency is the measurement of the number of times that a repeated event occurs per unit time. To calculate the frequency, one fixes a time interval, counts the number of occurrences of the event within that interval, and then divides this count by the length of the time interval.
In SI units, the result is measured in hertz (Hz) after the German physicist, Heinrich Rudolf Hertz. 1 Hz means that an event repeats once per second. Other units that have been used to measure frequency include: cycles per second, revolutions per minute (rpm).
Frequency of waves
[edit | edit source]Measuring the frequency of electromagnetic waves (such as light) the frequency in hertz is the number of cycles of the repetitive waveform per second. If the wave is a sound, frequency is what characterizes its pitch
Frequency has an inverse relationship to the concept of wavelength. The frequency f is equal to the speed v of the wave divided by the wavelength λ (lambda) of the wave:
In the special case of electromagnetic waves moving through a vacuum, then v = c, where c is the speed of light in a vacuum, and this expression becomes:
NOTE: Remember f=f When waves travel from one medium to another, their frequency remains more or less the same - only their wavelength changes.
Lawn mower analogy
[edit | edit source]To understand how light moves through a medium, such as glass, you can use the analogy of a person riding a self-powered lawnmower.
When the person is on the grass they slip and move slow. When they hit the pavement they stop slipping and speed up. The lawnmower moving over the grass is analogous to light moving through a medium, such as glass and the lawn mower moving over pavement is analogous to light moving through vacuum.
Furthermore when the lawn mower moves over the pavement and hits the grass at an angle one of the lawnmower's front wheel will hit the grass and slow down for a brief period while the other front wheel is going the same speed. This changes direction of the lawn mower. Much like a ray of light moving from vacuum to a medium such as glass changes direction when it hits the medium. The light ray bends towards the perpendicular.
Snell's Law
[edit | edit source]Snell's law is the simple formula used to calculate the refraction of light when travelling between two media of differing refractive index. It is named for its discoverer, Dutch mathematician Willebrord van Roijen Snell (1580-1626).
Overview
[edit | edit source]
In the diagram on the right, two media of refractive indices n1 (on the left) and n2 (on the right) meet at a surface or interface (vertical line). n2 > n1, and light has a slower phase velocity within the second medium.
A light ray PO in the leftmost medium strikes the interface at the point O. From point O, we project a straight line at right angles to the line of the interface; this is known as the normal to the surface (horizontal line). The angle between the normal and the light ray PO is known as the angle of incidence, θ1.
The ray continues through the interface into the medium on the right; this is shown as the ray OQ. The angle with which is makes to the normal is known of as the angle of refraction, θ2.
Snell's law gives the relation between the angles θ1 and θ2:
Note that, for the case of θ1 = 0° (i.e., a ray perpendicular to the interface) the solution is θ2 = 0° regardless of the values of n1 and n2. In other words, a ray entering a medium perpendicular to the surface is never bent.
The above is also valid for light going from a dense to a less dense medium; the symmetry of Snell's law shows that the same raypaths are applicable in opposite direction.
A qualitative rule for determining the direction of refraction is that the ray in the denser medium is always closer to the normal. A handy way to remember this is to visualize the ray as a car crossing the boundary between asphalt (the less dense medium) and mud (the denser medium). Depending on the angle, either the left wheel or the right wheel of the car will cross into the new medium first, causing the car to swerve.
Total internal reflection
[edit | edit source]When moving from a dense to a less dense medium (i.e. n1 > n2), it is easily verified that the above equation has no solution when θ1 exceeds a value known as the critical angle:
When θ1 > θcrit, no refracted ray appears, and the incident ray undergoes total internal reflection from the interface.
Given a normalized ray vector v and a normalized plane normal vector p, one can work out the normalized reflected and refracted rays: (note that the actual angles θ1 and θ2 are not worked out)
The cosines may be recycled and used in the Fresnel equations for working out the intensity of the resulting rays. The square root turns imaginary during total internal reflection, and the refracted ray is not real (there is apparently some kind of refracted ray, which decays very quickly, exponentially with distance).
Derivation
[edit | edit source]Snell's law may be derived from Fermat's principle, which states that the light travels the path which takes the least time. By taking the derivative of the optical path length, the stationary point is found giving the path taken by the light. In a classic analogy by Feynman, the area of lower refractive index is replaced by a beach, the area of higher refractive index by the sea, and the fastest way for a rescuer on the beach to get to a drowning person in the sea is to run along a path that follows Snell's law.







