Physics Course/Oscillation

Oscillation

Oscillation refers to any Periodic Motion moving at a distance about the equilibrium position and repeat itself over and over for a period of time . Example The Oscillation up and down of a Spring , The Oscillation side by side of a Spring. The Oscillation swinging side by side of a pendulum

Spring's Oscillation

Up and down Oscillation

When apply a force on an object of mass attach to a spring . The spring will move a distance y above and below the equilibrium point and this movement keeps on repeating itself for a period of time . The movement up and down of spring for a period of time is called Oscillation

Any force acting on an object can be expressed in a differential equation

$F = m \frac{d^2y}{dt^2}$

Equilibrium is reached when

F = - F_y

$F = m \frac{d^2y}{dt^2} = - k y$

$F = \frac{d^2y}{dt^2} + \frac{k}{m} y = 0$

$s^2 + \frac{k}{m} s = 0$

$s = \pm j \sqrt{\frac{k}{m}} t = \pm j \omega t = e^ j\omega t + e^ -j\omega t$

y = ASinωt

Side by Side Oscillation of Spring

When apply a force on an object of mass attach to a spring . The spring will move a distance x above and below the equilibrium point and this movement keeps on repeating itself for a period of time . The movement up and down of spring for a period of time is called Oscillation

Any force acting on an object can be expressed in a differential equation

$F = m \frac{d^2x}{dt^2}$

Equilibrium is reached when

F = - F_x

$F = m \frac{d^2x}{dt^2} = - k x$

$F = \frac{d^2x}{dt^2} + \frac{k}{m} x = 0$

$s^2 + \frac{k}{m} s = 0$

$s = \pm j \sqrt{\frac{k}{m}} t = \pm j \omega t = e^ j\omega t + e^ -j\omega t$

y = ASinωt

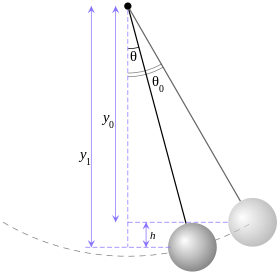
Swinging Oscillation from site to site of Pendulum

When there is a force acting on a pendulum. The pendulum will swing from side to side for a certain period of time . This type of movement is called oscillation

mg = − ly

$y = \frac{m g}{l}= v t$

$t =\frac{m g}{l v}$ ||

Summary

1. Oscillation is a periodic motion
2. Oscillation can be thought as a Sinusoidal Wave
3. Oscillation can be expressed by a mathematic 2nd order differential equation

Oscillation	Picture	Force	Acceleration	Distance travel	Time Travelled
Spring Oscillation	When there is a force acting on a spring . The spring goes into an up and down motion for a certain period of time . This type of movement is called oscillation	ma = − ky $m \frac{d^2y}{dt^2} = -ky$ $m \frac{d^2y}{dt^2} + ky = 0$ $s = \pm j \sqrt{\frac{k}{m}}$ $y = e^{j\sqrt{\frac{k}{m}}t} + e^{-j\sqrt{\frac{k}{m}}t}$ $y = y_m \cos \left(\sqrt{\frac{k}{m}}t\right)$	$a = \frac{k}{m}y$	$y = \frac{ma}{k}= a t^2$	$t = \pm\sqrt{\frac{k}{m}}$
Pendulum Oscillation	When there is a force acting on a pendulum. The pendulum will swing from side to side for a certain period of time . This type of movement is called oscillation	mg = − ly	$y = \frac{m g}{l}= v t$	$t =\frac{m g}{l v}$